Слайд 2Геометрии
Евклидова геометрия – геометрия на плоскости (изучение свойств жестких плоских фигур) или

в трёхмерном пространстве (изучение свойств жестких объёмных фигур)
Геометрия по Клейну – изучение свойств фигур в пространстве любого числа измерений, остающихся неизменными, или инвариантными, относительно любой заданной группы преобразований
Слайд 3Евклидова геометрия: допустимые преобразования
трансляции (перемещений с одного места на другое)
зеркальные отражения
повороты
сжатия

или растяжения
Слайд 4Геометрия по Клейну
Аффинная геометрия
Проективная геометрия
Топология
Теория множеств

Слайд 6Загадка Луны
Луна обращена к Земле всегда одной и той же стороной. Совершает

ли она полный оборот вокруг своей оси за то время, которое требуется ей, чтобы совершить полный оборот вокруг Земли?
Отец. Как астроном, я отвечу на этот вопрос утвердительно. Если бы мы наблюдали с Марса, то увидели бы, что Луна совершает один оборот вокруг своей оси всякий раз, когда она совершает полный оборот вокруг Земли.
Дочь. Ну посуди сам, папочка, как Луна может вращаться вокруг своей оси? Ведь если бы она вращалась, мы бы видели ее с разных сторон, а она всегда повернута к нам одной и той же стороной.
Слайд 7Итак, парадокс
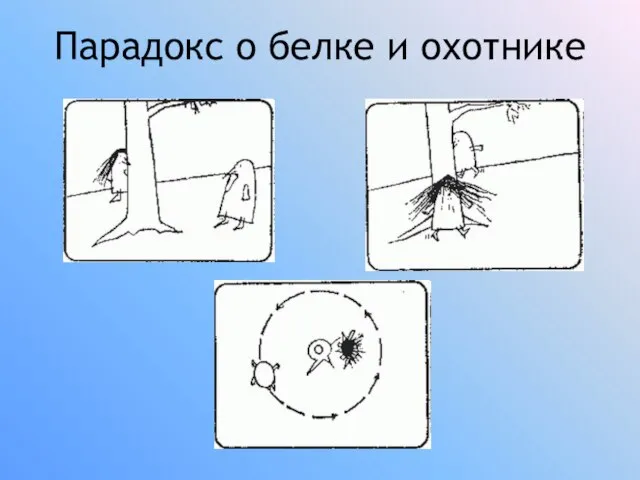
Итак, вращается ли Луна вокруг своей оси? Обходит ли парень вокруг

девушки, прячущейся от него за деревом? Настоящие ли это парадоксы, или в обоих случаях спор идет лишь о значении слова?
Начертите два соприкасающихся круга одного и того же радиуса. Представьте себе, что это два диска. Будем обкатывать один диск вокруг другого так, чтобы он не проскальзывал и ободы дисков все время соприкасались. Сколько раз повернется катящийся диск вокруг своей оси, пока совершит полный оборот вокруг неподвижного диска?
Слайд 8Кубики и прекрасная незнакомка
Сколько кубиков Вы видите: 6 или 7?

Слайд 9Кубики и прекрасная незнакомка
Кто изображён на картине: прекрасная незнакомка или старая ведьма?

Слайд 10Кубики и прекрасная незнакомка
Что вы здесь видите: куб, стоящий в углу комнаты,

куб, прилепленный извне к большому блоку, или выемку в форме куба в большом блоке?
Слайд 11Кубики и прекрасная незнакомка
А что здесь: два лица или чаша?

Слайд 12Мистер Рэнди и его необыкновенные ковры
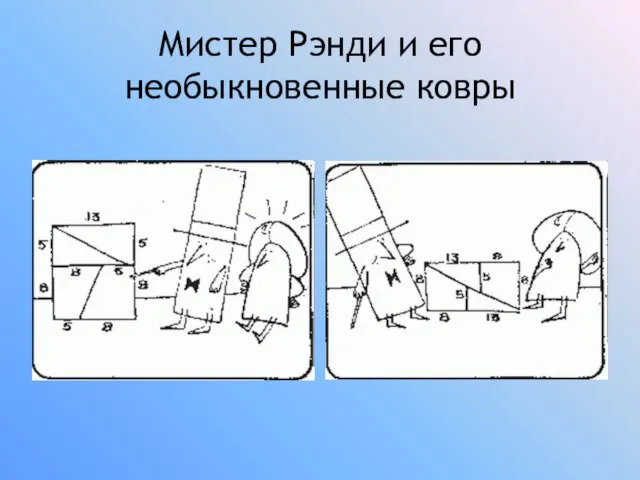
Слайд 13Мистер Рэнди и его необыкновенные ковры
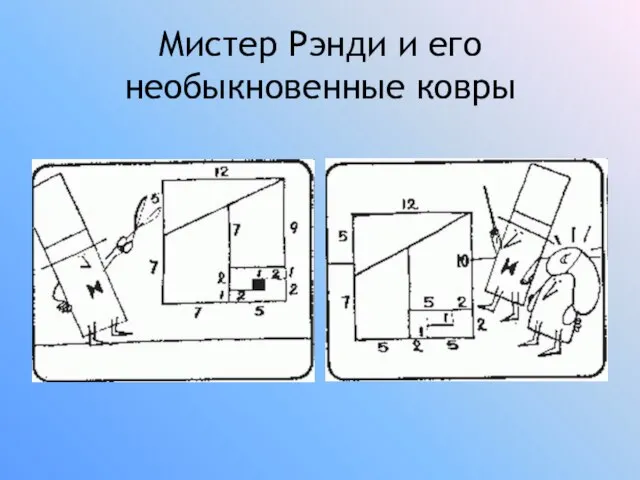
Слайд 17Невозможные объекты
Лестница Пенроуза

Слайд 19Невозможные объекты
Три или два зубца?












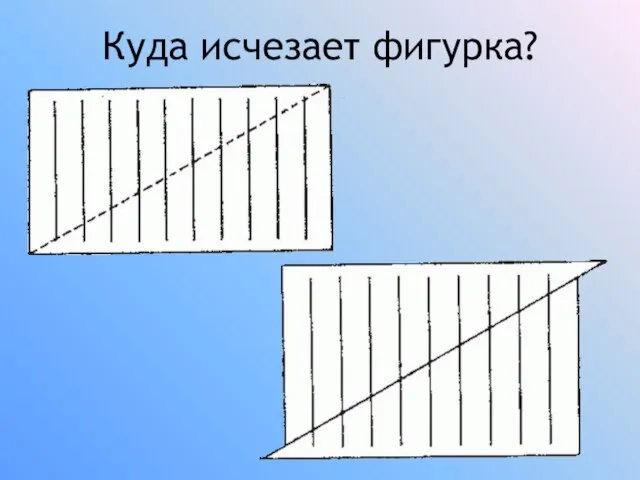




 Тема: «Спортивные игры зимой»
Тема: «Спортивные игры зимой» Список детей на получение кроватей и полотенец
Список детей на получение кроватей и полотенец Тепловые двигатели. Паровая турбина.
Тепловые двигатели. Паровая турбина. Система образования в Англии
Система образования в Англии Геометрические паркеты
Геометрические паркеты Подходы к системному целеполаганию. Лекция 2
Подходы к системному целеполаганию. Лекция 2 Конституция РФ
Конституция РФ Проект "Задачи на смеси и сплавы"
Проект "Задачи на смеси и сплавы" Раздел #. Дизайн интерьера
Раздел #. Дизайн интерьера Основы научных исследований
Основы научных исследований 000834aa-f5be4922
000834aa-f5be4922 Погружение
Погружение Невербальное общение
Невербальное общение Однородность керамзита
Однородность керамзита Презентация на тему Длина и меры ее измерения
Презентация на тему Длина и меры ее измерения Презентация на тему Экономика как наука
Презентация на тему Экономика как наука Кофемашина Yamaguchi CoffeeMann
Кофемашина Yamaguchi CoffeeMann Танковая викторина
Танковая викторина Петр Петрович Семёнов-Тян-Шанский
Петр Петрович Семёнов-Тян-Шанский Александр
Александр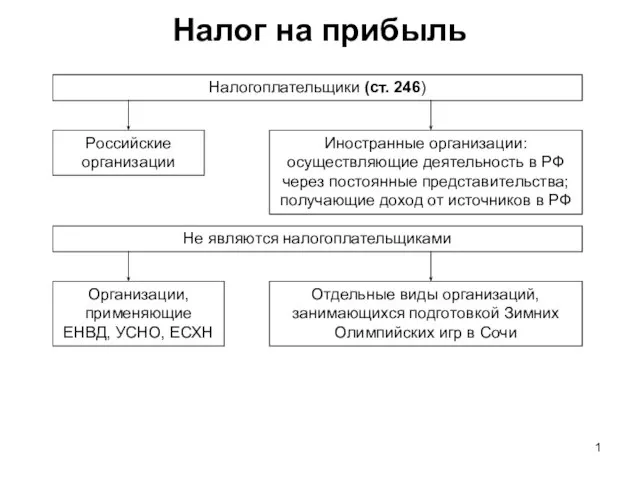 Налог на прибыль
Налог на прибыль SPORTS in Our Life
SPORTS in Our Life  Аудирование —цель и средство обучения
Аудирование —цель и средство обучения Отношения мужчины и женщины. Женская психология
Отношения мужчины и женщины. Женская психология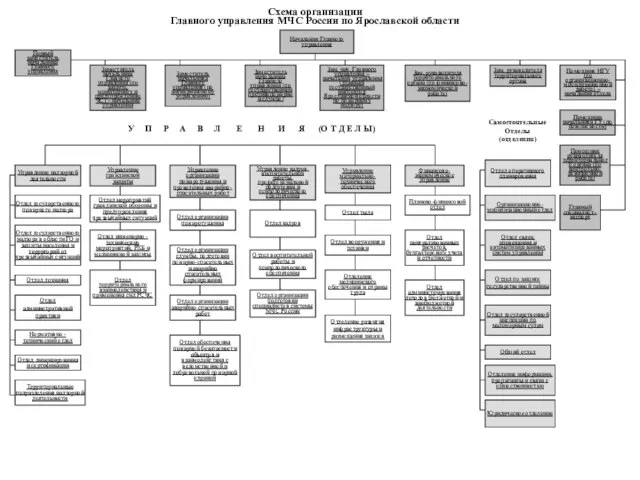 Схема организации Главного управления МЧС России по Ярославской области
Схема организации Главного управления МЧС России по Ярославской области Презентация на тему Афанасий Афанасьевич Фет (4 класс)
Презентация на тему Афанасий Афанасьевич Фет (4 класс) муниципальное образовательное учреждениеОбходская основная общеобразовательная школаУренского муниципального районаНижегор
муниципальное образовательное учреждениеОбходская основная общеобразовательная школаУренского муниципального районаНижегор куликовская битва
куликовская битва