Треугольники (5 класс)

Закончи предложение
1. Треугольником называется геометрическая фигура, состоящая из трех точек………
2. Точки А, В, С ∆АВС называются……………….
этого треугольника.
3. Два треугольника называются равными, если…….
не лежащих на одной прямой и трех отрезков попарно соединяющих эти точки.
вершинами
они при наложении совпадают

4. В равных треугольниках против равных сторон лежат…………..
5. Величина АВ + ВС + АС для ∆ АВС называется……………..
6.Если два треугольника равны, то их соответственные элементы……….
равные углы
периметром
равны

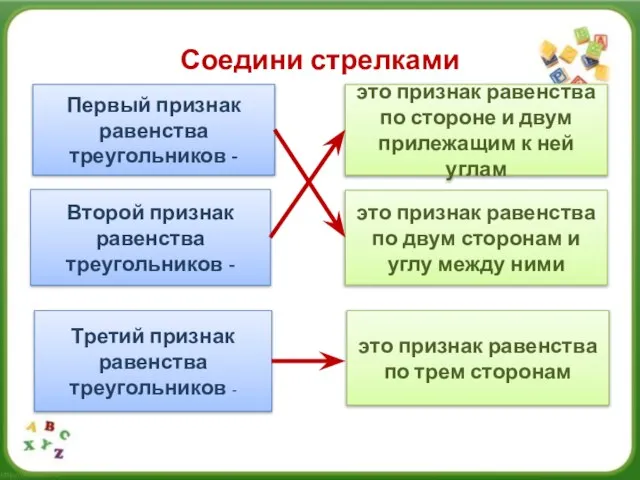
Соедини стрелками
Первый признак равенства треугольников -
Второй признак равенства треугольников -
Третий признак равенства треугольников -
это признак равенства по стороне и двум прилежащим к ней углам
это признак равенства по двум сторонам и углу между ними
это признак равенства по трем сторонам

Знак «+» правильные утверждения , знак «-» ошибочные
1. Если две прямые пересекаются под прямым углом, то они перпендикулярны.
2. При пересечении перпендикулярных прямых получается четыре тупых угла.
3. При пересечении перпендикулярных прямых получается четыре прямых угла.
4. Биссектриса любого треугольника – это прямая
+
-
+
-

5.Медианой треугольника, проведенной из данной вершины, называется отрезок, соединяющий эту вершину с серединой противолежащей стороны.
6. Биссектриса любого треугольника – это луч.
7.В любом треугольнике можно провести только одну биссектрису.
8. В любом треугольнике можно провести только три медианы
+
-
-
+

9.Высотой треугольника, опущенной из данной вершины, называется перпендикуляр, проведенный из этой вершины к прямой, содержащей противолежащую сторону треугольника.
10. В любом треугольнике можно провести сколько угодно высот.
11. В любом треугольнике биссектрисы пересекаются в одной точке.
+
-
+

Закончи предложение
1.Треугольник называется равнобедренным, если…….
2. Треугольник называется равносторонним, если…..
3. Равные стороны равнобедренного треугольника называются……
4. Третья сторона равнобедренного треугольника называется……..
две его стороны равны
все его стороны равны
называются боковыми
основанием

5. В равнобедренном треугольнике углы при основании …..
6. В равнобедренном треугольнике биссектриса , проведенная к основанию, является ……..
7. В равностороннем треугольнике все углы
……….
равны
медианой и высотой
равны

Теоретический тест
1. Медиана в равнобедренном треугольнике является его биссектрисой и высотой. Это утверждение:
а) всегда верно; б) может быть верно;
в) всегда неверно.
2. Если треугольник равносторонний, то:
а) он равнобедренный; б) все его углы равны; в) любая его высота является биссектрисой и медианой.

3. В каком треугольнике только одна его высота делит треугольник на два равных треугольника?
а) в любом; б) в равнобедренном ;
в) в равностороннем.
4. Биссектриса в равностороннем треугольнике является медианой и высотой. Это утверждение :
а) всегда верно; б) может быть верно;
в) всегда неверно.

5. Если треугольник равнобедренный, то:
а) он равносторонний ; б) любая его медиана является биссектрисой и высотой;
в) ответы а) и б) неверны.
6. В каком треугольнике любая его высота делит треугольник на два равных треугольника?
а) в любом; б) в равнобедренном;
в) в равностороннем