Содержание
- 2. Учебно-методическая литература ОСНОВНАЯ Опадчий, Ю. Ф. Аналоговая и цифровая электроника : учебник для вузов / Ю.
- 3. Учебно-методическая литература ДОПОЛНИТЕЛЬНАЯ Калабеков, Б. А. Цифровые устройства и микропроцессорные системы : учебник для ссузов. –
- 4. Логические переменные и Булева алгебра Переменные в алгебре логики могут принимать только ДВА значения: «0» и
- 5. Основные действия в Булевой алгебре ИЛИ (дизъюнкция) «+», «v» И (конъюнкция) НЕ (инверсия)
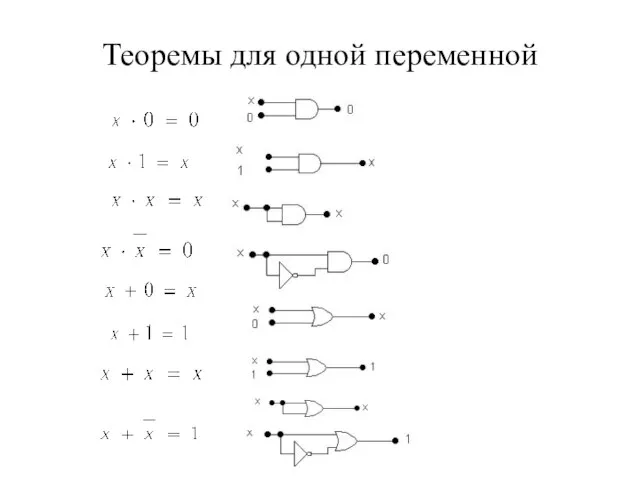
- 6. Теоремы для одной переменной 1) 2) 3) 4) 5) 6) 7) 8)
- 7. Законы Булевой алгебры Переместительный (Закон коммутативности)
- 8. 2. Сочетательный (Закон ассоциативности)
- 9. 3. Распределительный (Закон дистрибутивности)
- 10. 4. Закон поглощения
- 11. 5. Закон склеивания
- 12. 6. Закон отрицания (правило де Моргана)
- 13. Правило де Моргана справедливо для ЛЮБОГО числа переменных!!!
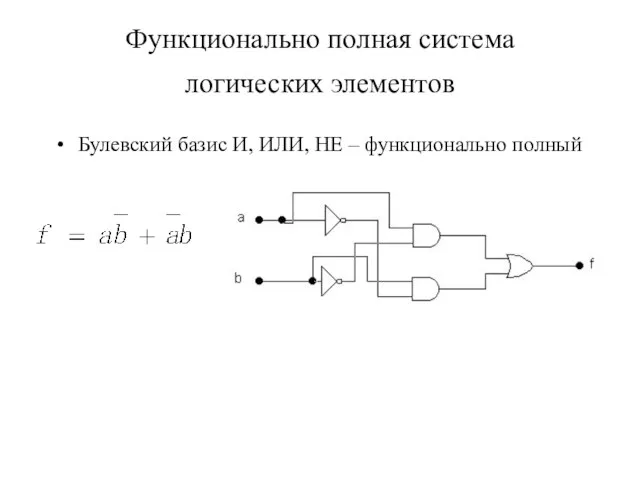
- 14. Функционально полная система логических элементов Булевский базис И, ИЛИ, НЕ – функционально полный
- 15. Логические элементы И-НЕ и ИЛИ-НЕ ИЛИ-НЕ НЕ: ИЛИ: И: (правило де Моргана) И-НЕ НЕ: И: ИЛИ:
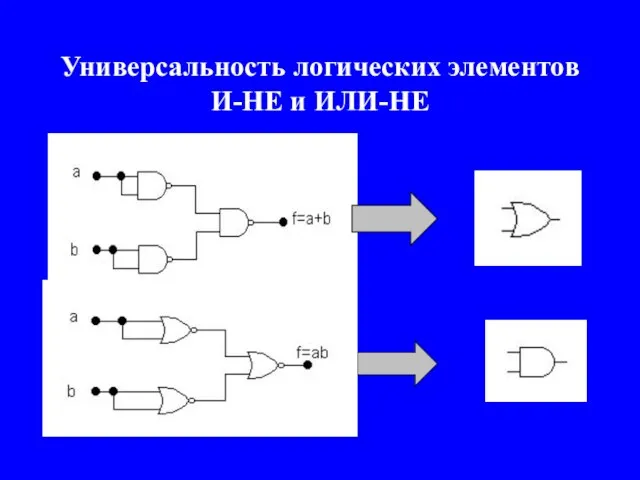
- 16. Универсальность логических элементов И-НЕ и ИЛИ-НЕ
- 17. Проектирование комбинационных логических схем (КЛС) Последовательность синтеза КЛС: составление таблицы истинности; запись булева выражения для требуемой
- 18. КЛС КЛС – это такая схема, выходные сигналы которой определяются исключительно действующими в данный момент времени
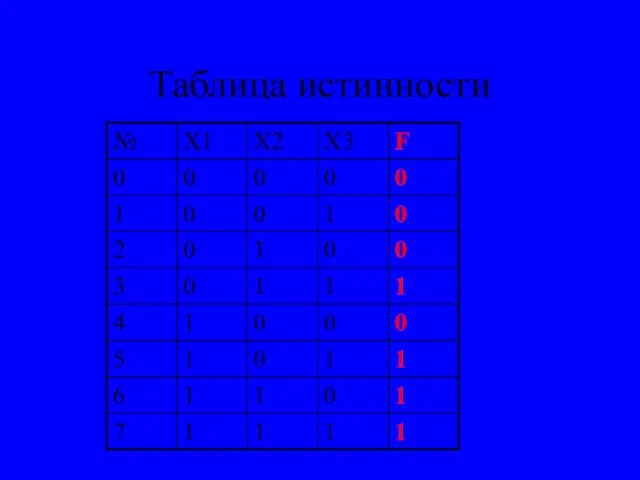
- 19. Таблица истинности
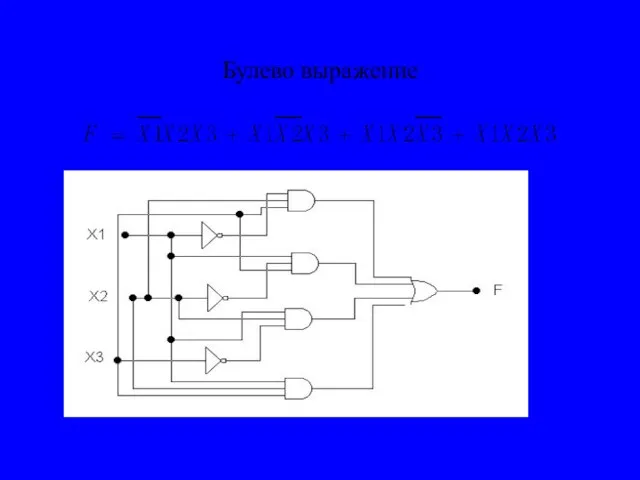
- 20. Булево выражение
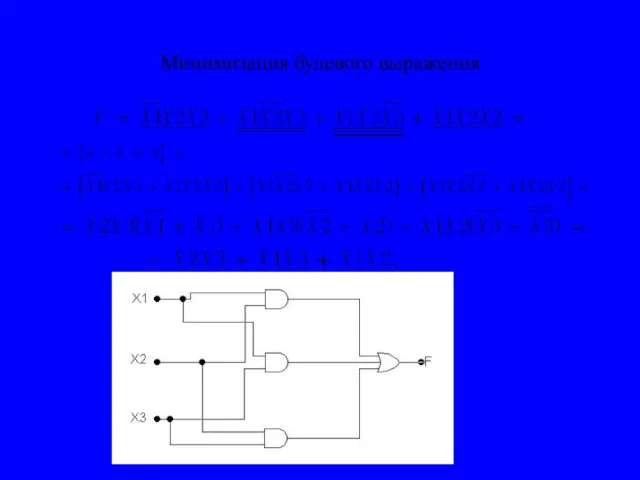
- 21. Минимизация булевого выражения
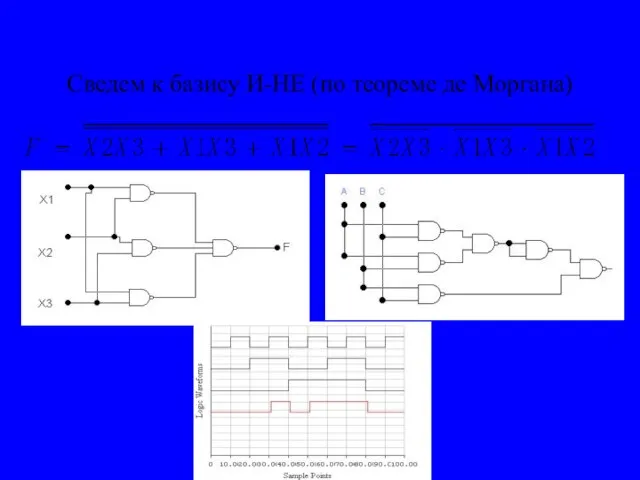
- 22. Сведем к базису И-НЕ (по теореме де Моргана)
- 23. Метод карт Карно Функцию следует привести к Дизъюнктивной Нормальной Форме (ДНФ – нормальная форма, в которой
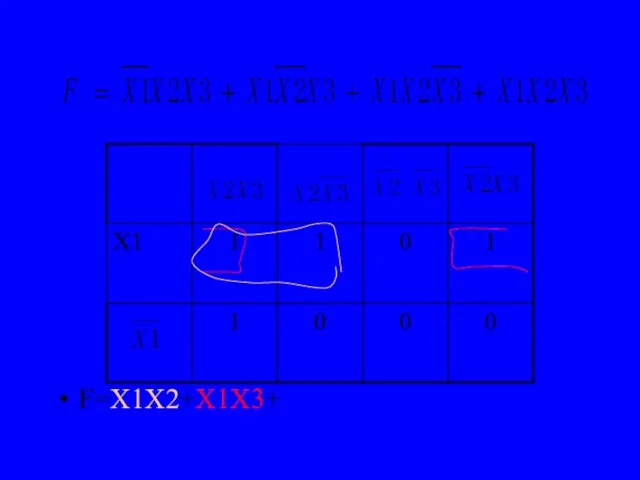
- 24. F=X1X2+X1X3+X2X3
- 26. Скачать презентацию







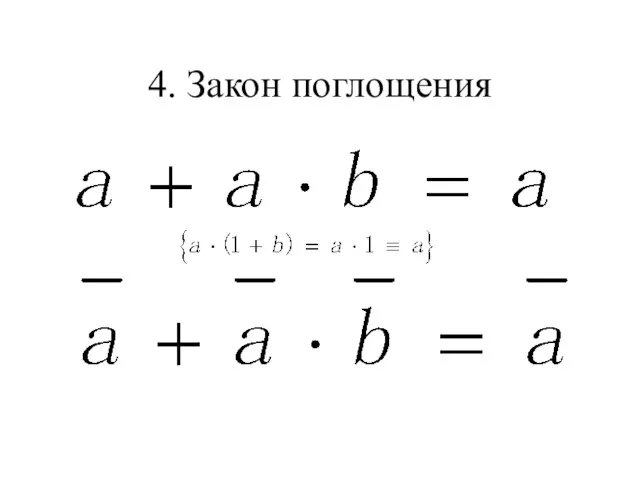
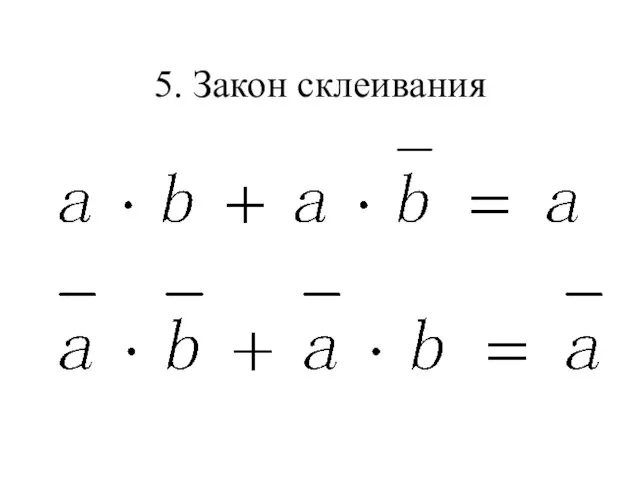






 Развитие регионального сервисабурового оборудования
Развитие регионального сервисабурового оборудования Урок русского языка 3 класс
Урок русского языка 3 класс Уровни стандартизации. Международный уровень
Уровни стандартизации. Международный уровень БудКАД – это мощная отечественная графическая система, позволяющая создавать профессиональные двумерные чертежи и трехмерные мо
БудКАД – это мощная отечественная графическая система, позволяющая создавать профессиональные двумерные чертежи и трехмерные мо Экзотические и перспективные виды электростанций
Экзотические и перспективные виды электростанций Развитие системы национальных статистических классификаций
Развитие системы национальных статистических классификаций «Управление персоналом и человеческий капитал современной России»
«Управление персоналом и человеческий капитал современной России» Когда вся жизнь человека - подвиг...
Когда вся жизнь человека - подвиг... План модернизации системы общего образования Тындинского района на 2012 год
План модернизации системы общего образования Тындинского района на 2012 год Вода океанов. Опреснение воды
Вода океанов. Опреснение воды 20,22.09
20,22.09 ЭКОНОМИЧЕСКИЙ МЕХАНИЗМ УЧАСТИЯ РОССИИ В ВТО НА РЕГИОНАЛЬНОМ УРОВНЕ
ЭКОНОМИЧЕСКИЙ МЕХАНИЗМ УЧАСТИЯ РОССИИ В ВТО НА РЕГИОНАЛЬНОМ УРОВНЕ Профсоюзная Халва
Профсоюзная Халва Стрит-арт. Дизайн
Стрит-арт. Дизайн Основы теории надежности. Тема 1: Основные понятия и определения
Основы теории надежности. Тема 1: Основные понятия и определения Увеличение и уменьшение числа на 2
Увеличение и уменьшение числа на 2 сложение и вычитание алг дробей
сложение и вычитание алг дробей Отличие управления персоналом от управления человеческими ресурсами
Отличие управления персоналом от управления человеческими ресурсами Структура питч-презентации
Структура питч-презентации ГБОУ Школа № 1381
ГБОУ Школа № 1381 Архитектура классицизма в России (11 класс)
Архитектура классицизма в России (11 класс) Управление территориальным развитием
Управление территориальным развитием Интеллектуальная игра по русскому языку
Интеллектуальная игра по русскому языку Манипуляторная техника
Манипуляторная техника Понятие документ в различных сферах человеческой деятельности
Понятие документ в различных сферах человеческой деятельности Бюджет 2022. 1 чтение. Муниципальное образование № 72
Бюджет 2022. 1 чтение. Муниципальное образование № 72 Flash движок в игре Зомби Ферма
Flash движок в игре Зомби Ферма Презентация на тему Соли
Презентация на тему Соли