Учебный курс Введение в параллельные алгоритмы

Введение в параллельные алгоритмы: Сортировка данных с точки зрения МВС (начало) © Якобовский М.В.
Ц Е Л Ь
О С Н О В Н А Я
Расположить в порядке
неубывания
N элементов массива чисел,
используя p процессоров
Москва, 2009 г.
из 34

Объём оперативной памяти одного процессорного узла достаточен для одновременного размещения в ней всех элементов массива
Объём оперативной памяти одного процессорного узла мал для одновременного размещения в ней всех элементов массива
Две задачи сортировки массива чисел
Введение в параллельные алгоритмы: Сортировка данных с точки зрения МВС (начало) © Якобовский М.В.
Москва, 2009 г.
из 34

Расположить N элементов массива a таким образом, чтобы для любого
выполнялось неравенство
Задача А
Введение в параллельные алгоритмы: Сортировка данных с точки зрения МВС (начало) © Якобовский М.В.
Москва, 2009 г.
из 34

Пусть массив можно разместить на p процессорах.
Пусть на процессоре с номером rank размещено
элементов массива .
Расположить N элементов массивов таким образом, чтобы:
для любых и
выполнялось неравенство
для любого
выполнялось неравенство
Задача B
Введение в параллельные алгоритмы: Сортировка данных с точки зрения МВС (начало) © Якобовский М.В.
Москва, 2009 г.
из 34

Части массива хранятся на нескольких процессорах
Каждая часть массива должна быть упорядочена
На процессорах с большими номерами должны быть размещены элементы массива с большими значениями
Правильно
Ошибка
Ошибка
Задача B
Введение в параллельные алгоритмы: Сортировка данных с точки зрения МВС (начало) © Якобовский М.В.
Москва, 2009 г.
из 34

Будем рассматривать только процесс упорядочивания элементов:
Перед началом сортировки на каждом из процессоров уже есть часть элементов массива
После окончания сортировки на каждом из процессоров должно остаться столько элементов, сколько их было в начале (но, это уже могут быть другие элементы, расположенные ранее на других процессорах)
Задача B
Введение в параллельные алгоритмы: Сортировка данных с точки зрения МВС (начало) © Якобовский М.В.
Москва, 2009 г.
из 34

Упорядочивание фрагментов массива на каждом из процессоров ?
Перераспределение элементов массива между процессорами
Упорядочивание фрагментов массива на каждом из процессоров ?
Этапы сортировки
Введение в параллельные алгоритмы: Сортировка данных с точки зрения МВС (начало) © Якобовский М.В.
Москва, 2009 г.
из 34

?
Конструирование наилучшего последовательного алгоритма
Введение в параллельные алгоритмы: Сортировка данных с точки зрения МВС (начало) © Якобовский М.В.
Москва, 2009 г.
из 34

Сравнение алгоритмов сортировки
Введение в параллельные алгоритмы: Сортировка данных с точки зрения МВС (начало) © Якобовский М.В.
Москва, 2009 г.

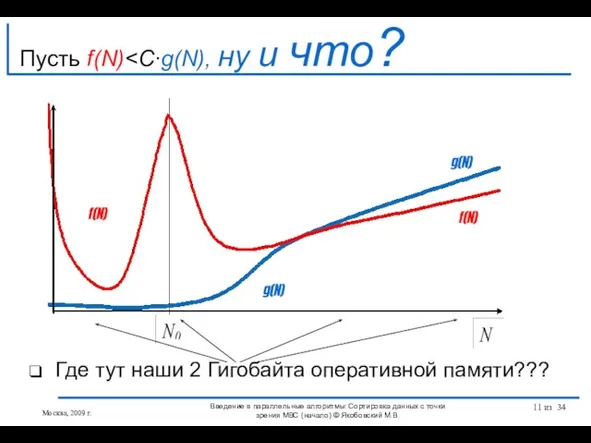
Пусть f(N)
Где тут наши 2 Гигобайта оперативной памяти???
f(N)
f(N)
g(N)
g(N)
Введение в параллельные алгоритмы: Сортировка данных с точки зрения МВС (начало) © Якобовский М.В.
Москва, 2009 г.
из 34

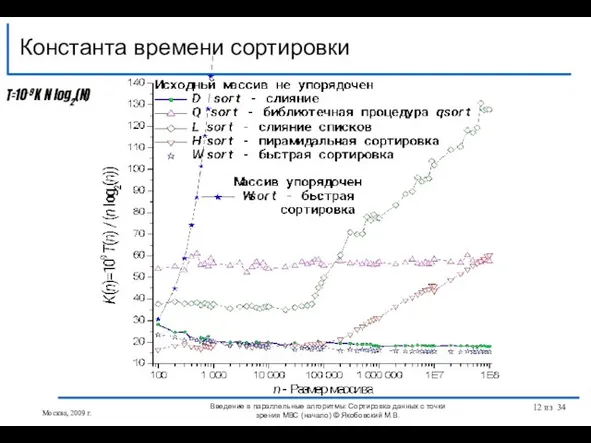
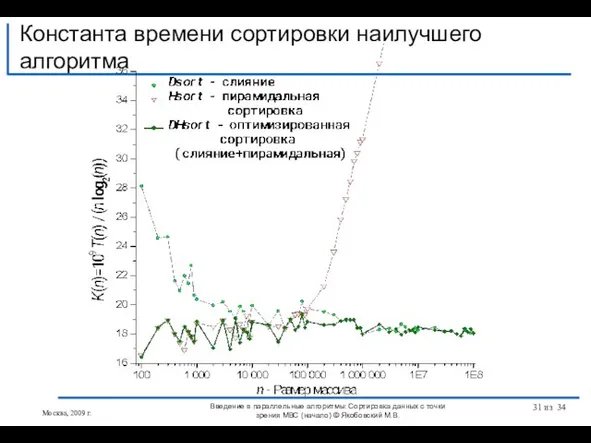
Константа времени сортировки
T=10-9K N log2(N)
Введение в параллельные алгоритмы: Сортировка данных с точки зрения МВС (начало) © Якобовский М.В.
Москва, 2009 г.
из 34

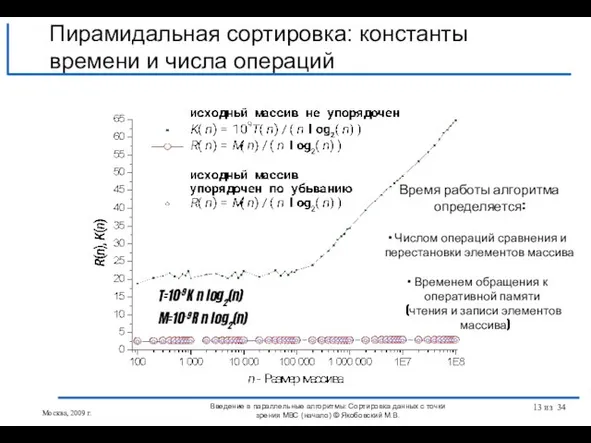
T=10-9K n log2(n)
M=10-9R n log2(n)
Пирамидальная сортировка: константы времени и числа операций
Введение в параллельные алгоритмы: Сортировка данных с точки зрения МВС (начало) © Якобовский М.В.
Москва, 2009 г.
Время работы алгоритма определяется:
Числом операций сравнения и перестановки элементов массива
Временем обращения к оперативной памяти (чтения и записи элементов
массива)
из 34

Введение в параллельные алгоритмы: Сортировка данных с точки зрения МВС (начало) © Якобовский М.В.
Москва, 2009 г.
Константа времени сортировки наилучшего алгоритма
из 34

сортировать ( массив mas, число элементов n )
{
если (n > 1)
{
// сортировка первой половины массива
сортировать ( mas, n/2);
// сортировка второй половины массива
сортировать ( mas+n/2, n-n/2);
// слияние отсортированных половинок массива
слияние ( mas, n/2, mas+n/2,n-n/2);
}
}
Введение в параллельные алгоритмы: Сортировка данных с точки зрения МВС (начало) © Якобовский М.В.
Москва, 2009 г.
Изящный алгоритм сортировки массива слиянием
из 34

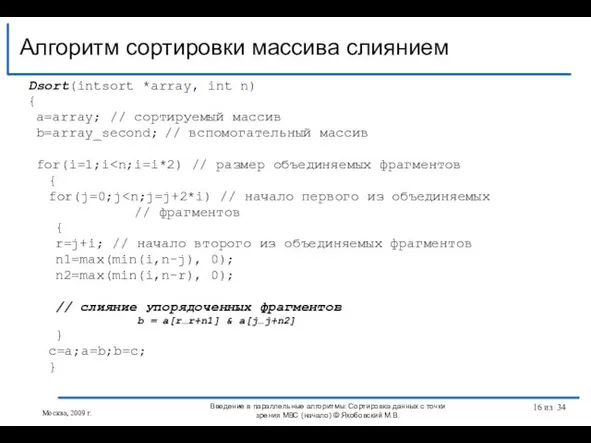
Dsort(intsort *array, int n)
{
a=array; // сортируемый массив
b=array_second; // вспомогательный массив
for(i=1;i размер объединяемых фрагментов
{
for(j=0;j
// фрагментов
{
r=j+i; // начало второго из объединяемых фрагментов
n1=max(min(i,n-j), 0);
n2=max(min(i,n-r), 0);
// слияние упорядоченных фрагментов
b = a[r…r+n1] & a[j…j+n2]
}
c=a;a=b;b=c;
}
Введение в параллельные алгоритмы: Сортировка данных с точки зрения МВС (начало) © Якобовский М.В.
Москва, 2009 г.
Алгоритм сортировки массива слиянием
из 34

Слияние упорядоченных фрагментов
for(ia=0,ib=0,k=0;k
{
if(ia>=n1) b[j+k]=a[r+ib++];
else
if(ib>=n2) b[j+k]=a[j+ia++];
else
if(a[j+ia]
else b[j+k]=a[r+ib++];
}
Введение в параллельные алгоритмы: Сортировка данных с точки зрения МВС (начало) © Якобовский М.В.
Москва, 2009 г.
из 34

Требуется 2 + 4 + 8 + 16 тактов (8 процессоров)
Сортировка слиянием методом сдваивания
Москва, 2009 г.
Введение в параллельные алгоритмы: Сортировка данных с точки зрения МВС (начало) © Якобовский М.В.
из 34
Для просмотра анимации возможно требуется установить свободно распространяемый Swiff Point Player: http://www.globfx.com/products/swfpoint/

Ускорение при методе сдваивания
Введение в параллельные алгоритмы: Сортировка данных с точки зрения МВС (начало) © Якобовский М.В.
Москва, 2009 г.
k1 – сортировка, k2 – передача данных
из 34

Требуется 8 тактов
Слияние двух массивов двумя процессорами
Москва, 2009 г.
Введение в параллельные алгоритмы: Сортировка данных с точки зрения МВС (начало) © Якобовский М.В.
из 34

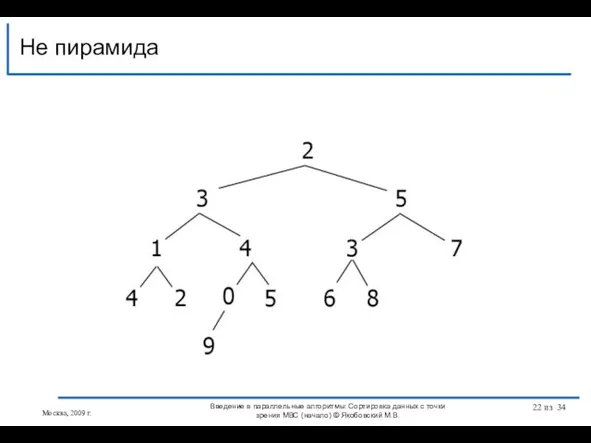
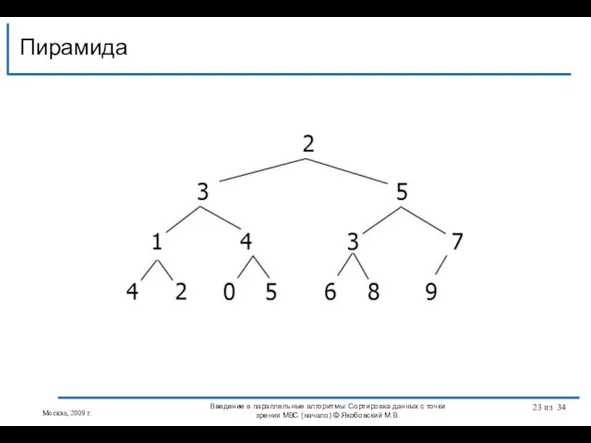
Дерево называют сбалансированным, если потомки любого его корня отличаются по высоте не более чем на 1
Пирамида – сбалансированное бинарное дерево в котором левый потомок любого узла не ниже правого потомка
Пирамиды
Москва, 2009 г.
Введение в параллельные алгоритмы: Сортировка данных с точки зрения МВС (начало) © Якобовский М.В.
из 34

Не пирамида
Москва, 2009 г.
Введение в параллельные алгоритмы: Сортировка данных с точки зрения МВС (начало) © Якобовский М.В.
из 34

Пирамида
Москва, 2009 г.
Введение в параллельные алгоритмы: Сортировка данных с точки зрения МВС (начало) © Якобовский М.В.
из 34

В линейном массиве потомки вершины i хранятся в элементах 2i, 2i+1
Хранение пирамиды
Москва, 2009 г.
Введение в параллельные алгоритмы: Сортировка данных с точки зрения МВС (начало) © Якобовский М.В.
из 34

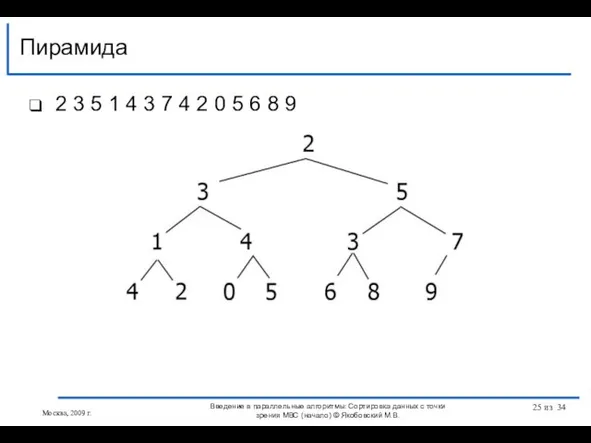
2 3 5 1 4 3 7 4 2 0 5 6 8 9
Пирамида
Москва, 2009 г.
Введение в параллельные алгоритмы: Сортировка данных с точки зрения МВС (начало) © Якобовский М.В.
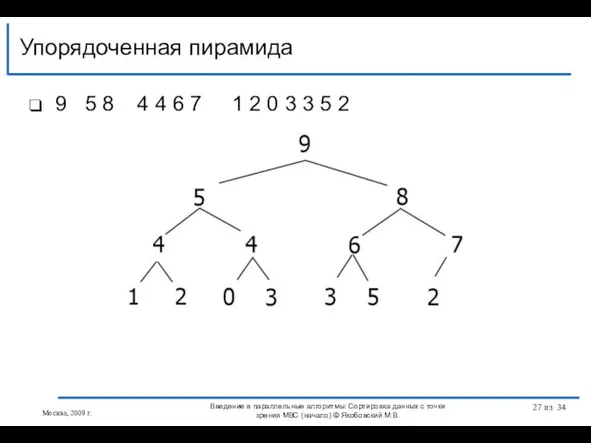
из 34

Пирамида называется упорядоченной если
для любого
(если такие элементы в массиве есть ☺)
Пирамидальная сортировка
Москва, 2009 г.
Введение в параллельные алгоритмы: Сортировка данных с точки зрения МВС (начало) © Якобовский М.В.
из 34

9 5 8 4 4 6 7 1 2 0 3 3 5 2
Упорядоченная пирамида
Москва, 2009 г.
Введение в параллельные алгоритмы: Сортировка данных с точки зрения МВС (начало) © Якобовский М.В.
из 34

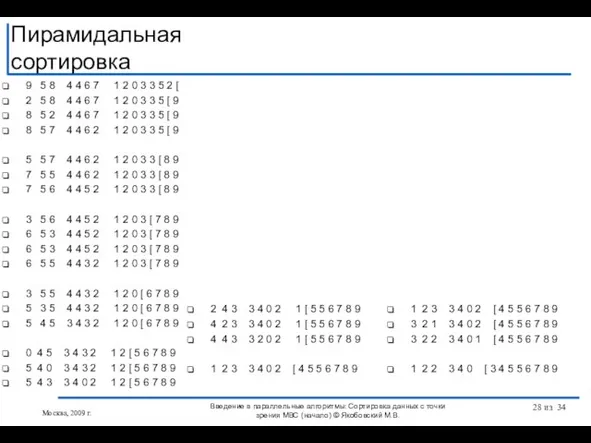
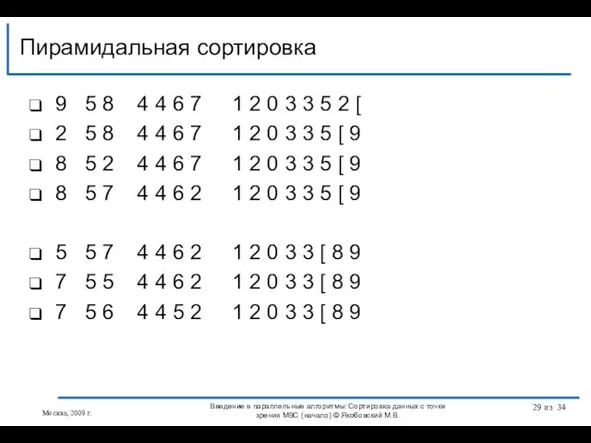
9 5 8 4 4 6 7 1 2 0 3 3 5 2 [
2 5 8 4 4 6 7 1 2 0 3 3 5 [ 9
8 5 2 4 4 6 7 1 2 0 3 3 5 [ 9
8 5 7 4 4 6 2 1 2 0 3 3 5 [ 9
5 5 7 4 4 6 2 1 2 0 3 3 [ 8 9
7 5 5 4 4 6 2 1 2 0 3 3 [ 8 9
7 5 6 4 4 5 2 1 2 0 3 3 [ 8 9
3 5 6 4 4 5 2 1 2 0 3 [ 7 8 9
6 5 3 4 4 5 2 1 2 0 3 [ 7 8 9
6 5 3 4 4 5 2 1 2 0 3 [ 7 8 9
6 5 5 4 4 3 2 1 2 0 3 [ 7 8 9
3 5 5 4 4 3 2 1 2 0 [ 6 7 8 9
5 3 5 4 4 3 2 1 2 0 [ 6 7 8 9
5 4 5 3 4 3 2 1 2 0 [ 6 7 8 9
0 4 5 3 4 3 2 1 2 [ 5 6 7 8 9
5 4 0 3 4 3 2 1 2 [ 5 6 7 8 9
5 4 3 3 4 0 2 1 2 [ 5 6 7 8 9
Пирамидальная
сортировка
Москва, 2009 г.
Введение в параллельные алгоритмы: Сортировка данных с точки зрения МВС (начало) © Якобовский М.В.
из 34
2 4 3 3 4 0 2 1 [ 5 5 6 7 8 9
4 2 3 3 4 0 2 1 [ 5 5 6 7 8 9
4 4 3 3 2 0 2 1 [ 5 5 6 7 8 9
1 2 3 3 4 0 2 [ 4 5 5 6 7 8 9
1 2 3 3 4 0 2 [ 4 5 5 6 7 8 9
3 2 1 3 4 0 2 [ 4 5 5 6 7 8 9
3 2 2 3 4 0 1 [ 4 5 5 6 7 8 9
1 2 2 3 4 0 [ 3 4 5 5 6 7 8 9

9 5 8 4 4 6 7 1 2 0 3 3 5 2 [
2 5 8 4 4 6 7 1 2 0 3 3 5 [ 9
8 5 2 4 4 6 7 1 2 0 3 3 5 [ 9
8 5 7 4 4 6 2 1 2 0 3 3 5 [ 9
5 5 7 4 4 6 2 1 2 0 3 3 [ 8 9
7 5 5 4 4 6 2 1 2 0 3 3 [ 8 9
7 5 6 4 4 5 2 1 2 0 3 3 [ 8 9
Пирамидальная сортировка
Москва, 2009 г.
Введение в параллельные алгоритмы: Сортировка данных с точки зрения МВС (начало) © Якобовский М.В.
из 34

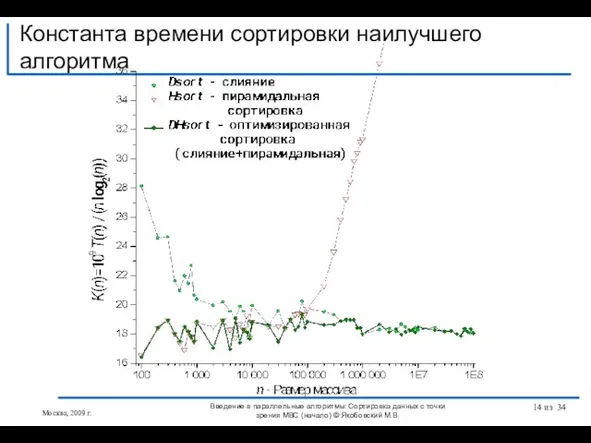
Оптимальный алгоритм
Оптимальна комбинация
H алгоритма (пирамидальная )
в диапазоне
10 - 50 000
D алгоритма (слияние) в диапазоне
50 000 - 100 000 000
Введение в параллельные алгоритмы: Сортировка данных с точки зрения МВС (начало) © Якобовский М.В.
Москва, 2009 г.
из 34

Введение в параллельные алгоритмы: Сортировка данных с точки зрения МВС (начало) © Якобовский М.В.
Москва, 2009 г.
Константа времени сортировки наилучшего алгоритма
из 34

Рассмотрен ряд методов сортировки массивов
Проиллюстрирована разница между зависимостью от объема данных времени сортировки и числа выполняемых операций
Построен «наилучший» последовательный алгоритм сортировки
Заключение
Введение в параллельные алгоритмы: Сортировка данных с точки зрения МВС (начало) © Якобовский М.В.
Москва, 2009 г.
из 34

В чем причина различия характера зависимости времени сортировки и числа выполняемых операций от числа элементов сортируемого массива?
Какие еще можно предложить варианты сортировки, улучшающие использование кеш- памяти?
Вопросы для обсуждения
Введение в параллельные алгоритмы: Сортировка данных с точки зрения МВС (начало) © Якобовский М.В.
Москва, 2009 г.
из 34