Слайд 2ЛЕКЦИЯ 1
Предмет
«Математический анализ»
Вещественные числа

Слайд 4Немного из истории
Школа Вейерштрасса
теория действительных (вещественных)
чисел как бесконечных

десятичных дробей
Школа Кантора
теория действительных (вещественных)
чисел как сечение в множестве рациональных чисел,
завершающаяся сечением в множестве действительных
чисел
Школа Дедекинда
теория действительных (вещественных)
как теория фундаментальных
последовательностей рациональных чисел
Слайд 5продолжение
Карл Теодор Вейерштрасс
1815 – 1897
немецкий математик
Боннский университет
(специального высшего образования не

имел)
Слайд 6продолжение
Георг Кантор
1845 – 1918
немецкий математик
Берлинский университет

Слайд 7продолжение
Рихард Юлиус Дедекинд
1831 – 1916
немецкий математик
Геттинский университет

Слайд 8 I. Предмет «Математический анализ»
Три части
Теория пределов
Дифференциальное исчисление
Интегральное исчисление
Три операции
Предельный переход

(вычисление пределов)
Дифференцирование
(нахождение дифференциала, производной)
Интегрирование
(нахождение интеграла)
Слайд 9 продолжение
Математический анализ
(анализ бесконечно малых величин)
Анализ и исследование функций
Действительные (вещественные) числа
Теория

пределов
Дифференциальное и интегральное исчисления функции одной и нескольких переменных
Ряды
Теория поля
Слайд 12Символика (логические кванторы или символы)

Слайд 18 5. Метод математической индукции






























 Печатное устройство HP DeskJet GT 5810/5820
Печатное устройство HP DeskJet GT 5810/5820 Год науки и технологий
Год науки и технологий Кофе Пётр Великий Пётр Великий в зёрнах. 100г, 250г, 500г, 500г, 1000г Смесь отборных зёрен разных сортов Арабики средней обжарки. Пётр Велик
Кофе Пётр Великий Пётр Великий в зёрнах. 100г, 250г, 500г, 500г, 1000г Смесь отборных зёрен разных сортов Арабики средней обжарки. Пётр Велик Человек и природа в лирике М.Ю.Лермонтова
Человек и природа в лирике М.Ю.Лермонтова 8 Букви е, и в особових закiнченнях
8 Букви е, и в особових закiнченнях Семейство Крестоцветные
Семейство Крестоцветные Государственная символика России и Чувашской Республики
Государственная символика России и Чувашской Республики Тест: Туристский поход с проверкой туристских навыков. АУ Управление спортивных сооружений Республики Марий Эл
Тест: Туристский поход с проверкой туристских навыков. АУ Управление спортивных сооружений Республики Марий Эл Учитель физики, химии и информатики МОУ СОШ с.Каринка Кирово-Чепецкого района
Учитель физики, химии и информатики МОУ СОШ с.Каринка Кирово-Чепецкого района  Технический анализ товарных и финансовых рынков Индикаторы
Технический анализ товарных и финансовых рынков Индикаторы МИР КАК ФОРМА И ПОТРЕБЛЕНИЕ
МИР КАК ФОРМА И ПОТРЕБЛЕНИЕ Моя семья – моё богатство Семья Орловых
Моя семья – моё богатство Семья Орловых Куприенко Игорь Витальевич Член Координационного совета
Куприенко Игорь Витальевич Член Координационного совета ВОДА
ВОДА Название презентации
Название презентации Переправа
Переправа Электронное правительство. Международные рейтинги и критерии оценки.
Электронное правительство. Международные рейтинги и критерии оценки. Парфюм от Эйвон Тудей
Парфюм от Эйвон Тудей Распознавание растений разных отделов
Распознавание растений разных отделов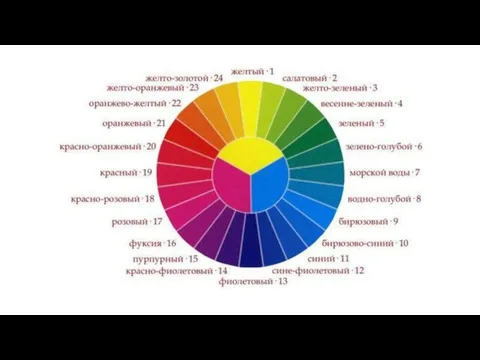 Цветовой круг
Цветовой круг Профессия - пластический хирург
Профессия - пластический хирург Использование технологии дополненной реальности в образовании
Использование технологии дополненной реальности в образовании Мастер – класс Изготовление картин из цветного опила
Мастер – класс Изготовление картин из цветного опила Family memory book
Family memory book  ТЕМА: «Кто такие птицы?»
ТЕМА: «Кто такие птицы?» Делаем отчет. Занятие 8
Делаем отчет. Занятие 8 Викторина
Викторина Восстановление автомобильных деталей сваркой и наплавкой
Восстановление автомобильных деталей сваркой и наплавкой