Удивительные числа

Объект нашего исследования – натуральные числа.
Предмет исследования
– свойства этих чисел.
Гипотеза: Если простые числа – это «кирпичики», из которых строятся все натуральные числа, то, «перекладывая» их, можно получить удивительные «числовые сооружения».

Цель исследования:
Познакомиться с удивительными числами и установить роль простых чисел в изменении их свойств.
Задачи:
Описать способы поиска простых чисел.
Рассмотреть свойства совершенных и дружественных чисел.
Познакомиться с палиндромами и репьюнитами.
Метод исследования – теоретический

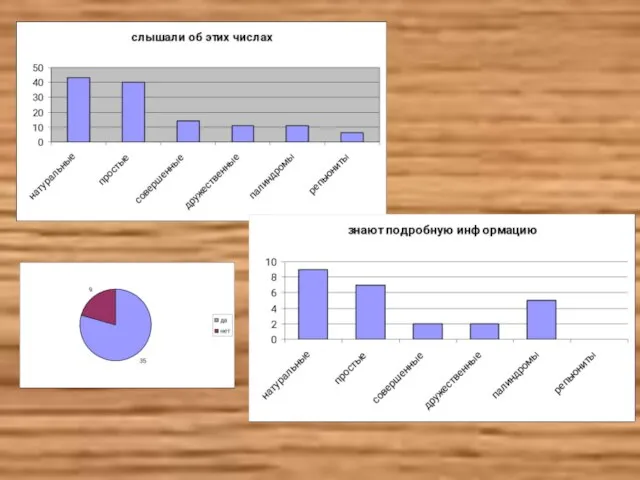
Простые числа
Числа, которые имеют только два различных делителя, называются простыми
7=1·7
23=1·23
Самое маленькое простое число. Единственное четное среди простых
2

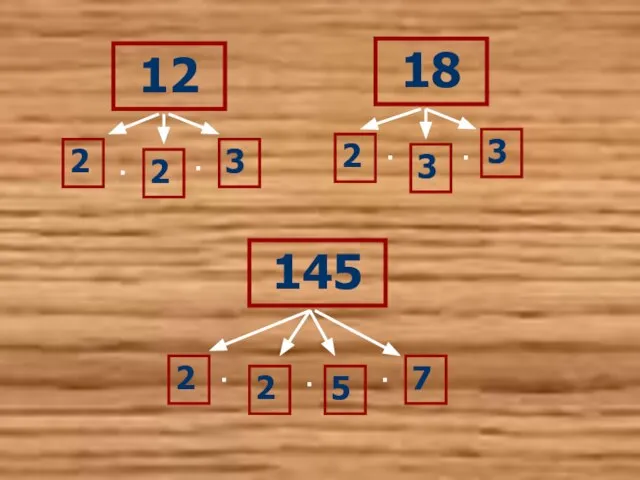
12
2
2
3
·
·
18
2
3
3
·
·
145
2
2
5
7
·
·
·

Эратосфен

близнецы

Пьер Ферма
1601-1665
P=22 + 1
n

Совершенные числа
Натуральное число n называется совершенным, если сумма всех его собственных делителей, отличных от самого n, в точности равна n.
6
+
+
6
28
2
4
7
1
14
+
+
+
+
28

Совершенные числа
6, 28, 496, 8128, 33550336…
Вот 25-е число: 244496 . (244496-1)
26 790 цифр!!!

Пифагор
220 и 284
220
1
2
2
5
11
1+2+4+5+10+11+20+22+44+55+110=284
284
1
2
2
71
1+2+4+71+142=220

Дружественные числа
Если сумма собственных делителей одного числа равна второму числу и, наоборот, сумма собственных делителей второго числа равна первому, то такие числа называют дружественными

Палиндромы и репьюниты
Обращенное число – это число, записанное теми же цифрами, но расположенными в обратном порядке. Например, 1234 обращенное 4321.
Палиндромическое число - равное обращенному.
Например, 121, 5995, 12321
Репьюниты - натуральные числа, запись которых состоит только из единиц.
В десятичной системе счисления репьюниты обозначаются короче: R1=1, R2=11, R3=111, R4=1111…

R2, R19, R23, R317 и R1031 – простые числа
111=3∙ 37;
1111=11∙101
11111=41∙271
111111=3∙7∙ 11∙13∙37
1111111=239∙ 4649 и т. д.
11∙11=121
11∙111=1221
1111∙11=12221
1112=12321

ВЫВОД
простые числа – это «кирпичики», из которых строятся все
натуральные числа. «перекладывая» их, можно получить удивительные «числовые сооружения»:
СОВЕРШЕННЫЕ ЧИСЛА,
ДРУЖЕСТВЕННЫЕ, РЕПЬЮНИТЫ