Умножение натуральных чисел

Проверка экипажа:
1 вариант.
Записать все числа от 1 до 60 которые без остатка делятся на 6.
2 вариант.
Записать все числа от 1 до 70 которые без остатка делятся на 7.
6, 12, 18 ,24, 30, 36, 42, 48, 54, 60
7, 14, 21, 28, 35, 42, 49, 56, 63, 70

Показания приборов:
60
Молодцы!

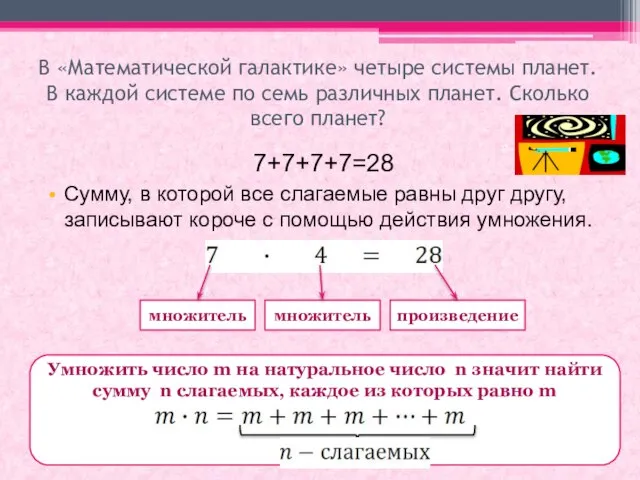
В «Математической галактике» четыре системы планет. В каждой системе по семь различных планет. Сколько всего планет?
7+7+7+7=28
Сумму, в которой все слагаемые равны друг другу, записывают короче с помощью действия умножения.
множитель
множитель
произведение
Умножить число m на натуральное число n значит найти сумму n слагаемых, каждое из которых равно m

Планета «Умножение натуральных чисел».
№404.
№405.

№ 412 (а,б,в,д,е,ж)
Молодцы!