Содержание
- 2. Цели урока: рассмотреть различные случаи взаимного расположения прямой и окружности; совершенствовать у учащихся навыки решения задач.
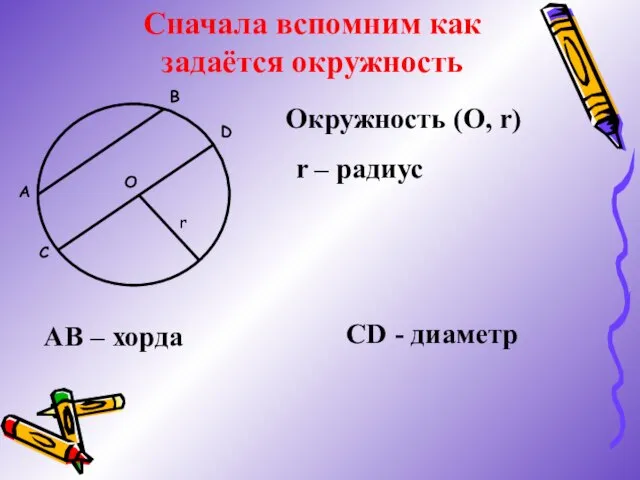
- 3. Сначала вспомним как задаётся окружность A B О С D r Окружность (О, r) r –
- 4. Решение задач по готовым чертежам (устно) 1. А С О К Найти угол АОК
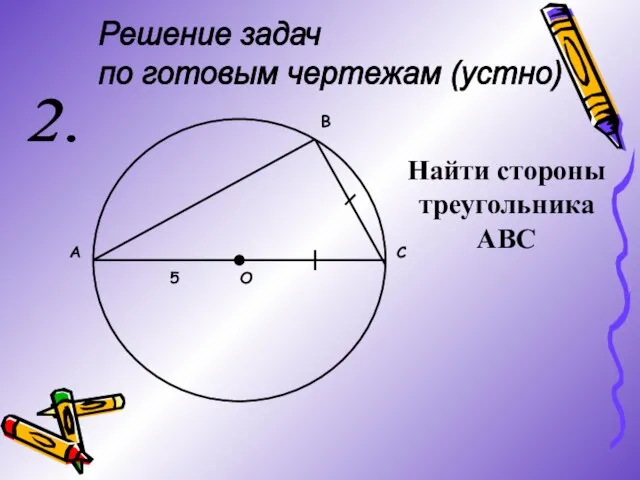
- 5. Решение задач по готовым чертежам (устно) 2. А С В О 5 Найти стороны треугольника АВС
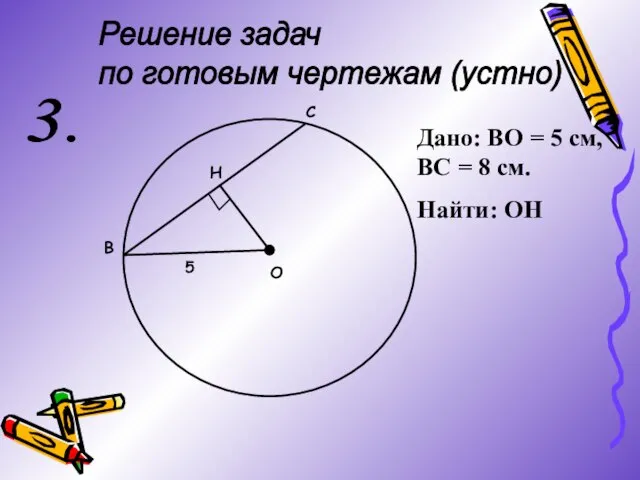
- 6. Решение задач по готовым чертежам (устно) 3. О В С Н 5 Дано: ВО = 5
- 7. Решение задач по готовым чертежам (устно) 4. О А Даны окружность с центром О и точка
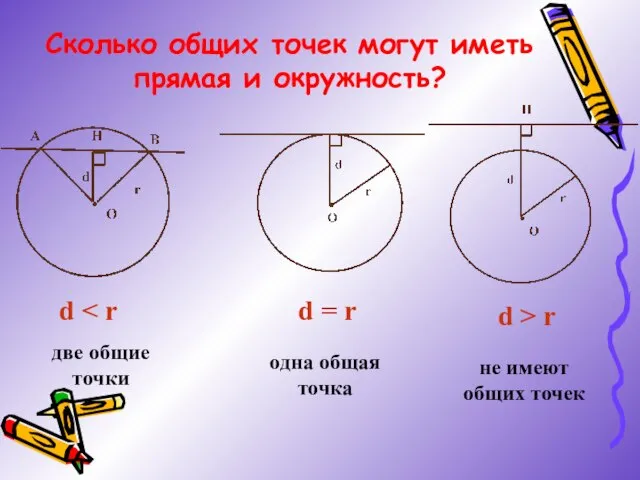
- 8. Как вы думаете, сколько общих точек могут иметь прямая и окружность? О а r Даны окружность
- 9. 1) d O H A B d p По теореме Пифагора Следовательно, точки А и В
- 10. 2) d=r p O H М d=r ОН=r, точка Н лежит на окружности и, значит, является
- 11. 3) d>r O p М H d>r r ОН>r, поэтому для любой точки М прямой р
- 12. Сколько общих точек могут иметь прямая и окружность? d d = r d > r две
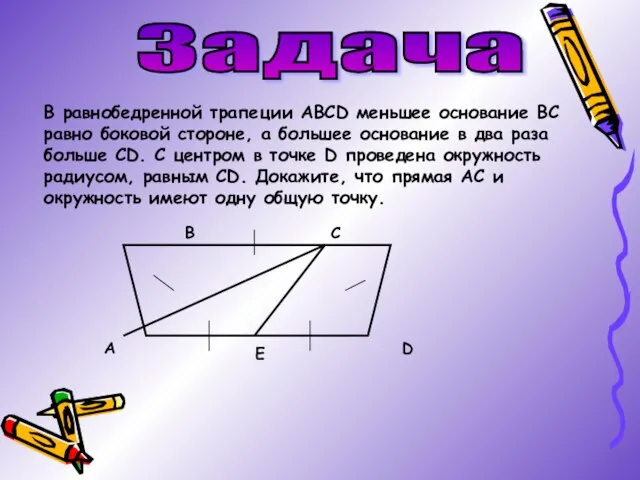
- 13. Задача В равнобедренной трапеции АВСD меньшее основание ВС равно боковой стороне, а большее основание в два
- 15. Скачать презентацию







 и формирование отчетности
и формирование отчетности Презентация на тему Швейные товары
Презентация на тему Швейные товары  Филологи
Филологи АУДИТ
АУДИТ Проектирование СКС коттеджного участка из бруса
Проектирование СКС коттеджного участка из бруса Интеграция риск-менеджмента в ключевые процессы принятия решений
Интеграция риск-менеджмента в ключевые процессы принятия решений Проект: Юридическое сопровождение дополнительной эмиссии обыкновенных акций, размещаемых по открытой подписке
Проект: Юридическое сопровождение дополнительной эмиссии обыкновенных акций, размещаемых по открытой подписке Выполненное и планируемое благоустройство
Выполненное и планируемое благоустройство Вопросы составления и заверения отчетности получателей бюджетных средств в территориальных органах Федерального казначейства
Вопросы составления и заверения отчетности получателей бюджетных средств в территориальных органах Федерального казначейства Чудесные превращения воды в природе (3 класс)
Чудесные превращения воды в природе (3 класс) Волга – главный символ нашего края
Волга – главный символ нашего края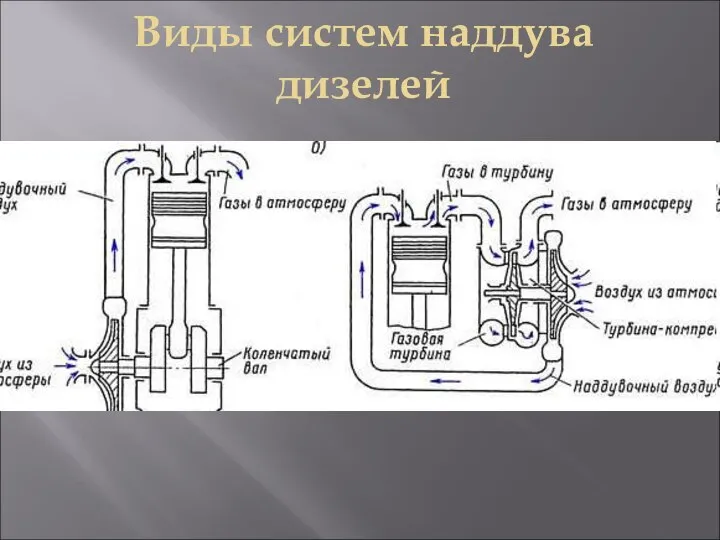 Виды систем наддува дизелей на судне. Аксиально-поршневой насос
Виды систем наддува дизелей на судне. Аксиально-поршневой насос Гражданское общество. Задания для выполнения
Гражданское общество. Задания для выполнения Природные и экологические опасности
Природные и экологические опасности London
London  Семейное право
Семейное право Morphonologie der Verben IPrasens
Morphonologie der Verben IPrasens Www.auditexpo.ru. Основные типы клиентов: Аналитический - ключевой вопрос: «Как?», «Зачем?» Рассудителен, Логичен, Собран, Нужны детали, Изуч
Www.auditexpo.ru. Основные типы клиентов: Аналитический - ключевой вопрос: «Как?», «Зачем?» Рассудителен, Логичен, Собран, Нужны детали, Изуч Мотивация продавцов-промоутеров SEB
Мотивация продавцов-промоутеров SEB Выражение характера человека в изображении. Женский образ русских сказок
Выражение характера человека в изображении. Женский образ русских сказок Портфолио
Портфолио Школьный музей "Родные истоки"
Школьный музей "Родные истоки" Тип, имя и значение переменной
Тип, имя и значение переменной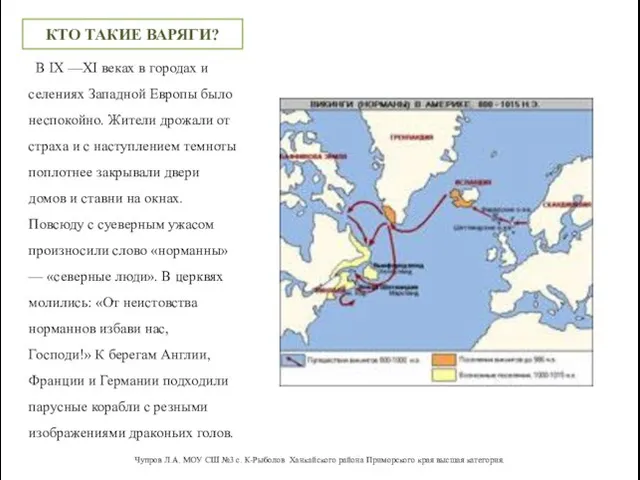 Путь из Варяг в Греки
Путь из Варяг в Греки Масштабируемое решениеот ЛПУ до региона
Масштабируемое решениеот ЛПУ до региона Агроэкосистеемы, или аграрные экологические системы
Агроэкосистеемы, или аграрные экологические системы Религия как одна из форм культуры
Религия как одна из форм культуры Угольная кислота
Угольная кислота