Содержание
- 2. y’’ = f(x,y,y’). y = ϕ(x,C’,C’’), Общее решение где С’,С’’ - независимые постоянные, Тогда начальные условия:
- 3. Пусть имеем линейное дифференциальное однородное уравнение y’’ + p⋅y’ + q⋅y = 0. (2.8) где p,
- 4. так называемое характеристическое уравнение
- 5. Для составления характеристического уравнения достаточно в уравнении производные у’’, у’ и саму функцию у заменить на
- 6. . , : ; 1. следовательно, имеем два действительных корня k1 и k2. Следовательно, уравнение допускает
- 7. Определение. Два решения у1 и у2 называются линейно зависимыми, если можно подобрать постоянные числа а1 и
- 8. , . : . . 2. , следовательно, В этом случае корень называется кратным, и частное
- 9. . y’’ + p⋅y’ + q⋅y = 0
- 10. . или Следовательно, z’’ = 0.
- 11. Тогда z’ = a и z = ax + b, где a и b - произвольные
- 12. 3. , то будем иметь два сопряженных комплексных корня и . . k1 = α +
- 13. Пусть дано дифференциальное уравнение y’’ + p⋅y’ + q⋅y = 0 1. Если характеристическое уравнение имеет
- 15. Скачать презентацию


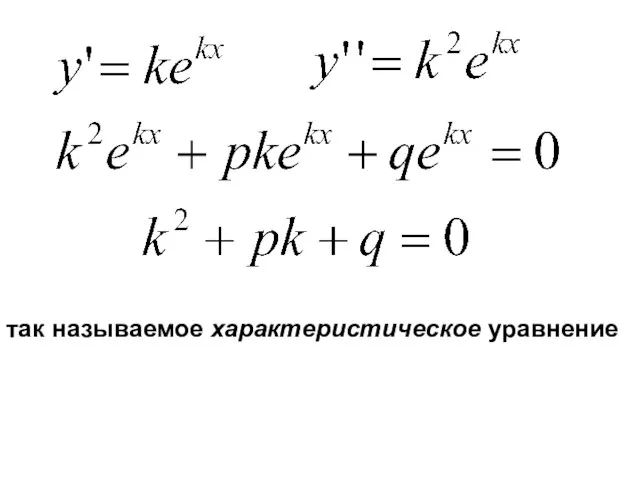




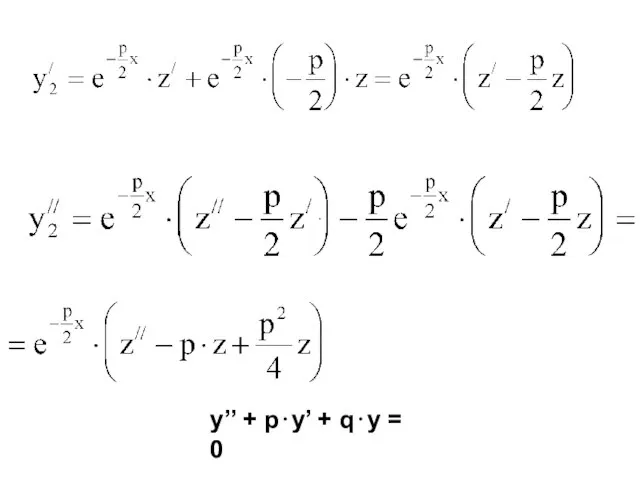




 ЧС в быту
ЧС в быту Пустыни
Пустыни Проект группы “Б”
Проект группы “Б” Древние люди Забайкалья
Древние люди Забайкалья 1816 г. Рене-Теофиль Лаэннек изобрёл стетоскоп
1816 г. Рене-Теофиль Лаэннек изобрёл стетоскоп Образовательная программа по вопросам ценообразования и государственного регулирования отраслей экономики РФ
Образовательная программа по вопросам ценообразования и государственного регулирования отраслей экономики РФ СОДЕРЖАНИЕ: Краткая информация………………………………………33 Партнеры………………..……………………………………44 Стадии процесса…..………………
СОДЕРЖАНИЕ: Краткая информация………………………………………33 Партнеры………………..……………………………………44 Стадии процесса…..……………… Инфекции — Туляремия
Инфекции — Туляремия Презентация на тему Автомеханик
Презентация на тему Автомеханик Организация проектной деятельности на уроках
Организация проектной деятельности на уроках Однокомнатная квартира. Тип 1
Однокомнатная квартира. Тип 1 «Учителя – в годы Великой Отечественной войны» Экспозиция школьного музеявыполнена зам. директора по ВР Мельниченко В.В.С.Нарв
«Учителя – в годы Великой Отечественной войны» Экспозиция школьного музеявыполнена зам. директора по ВР Мельниченко В.В.С.Нарв Растительный мир тундры
Растительный мир тундры Строительный подряд
Строительный подряд Еженедельная газета «ЮРИДИЧЕСКАЯ ПРАКТИКА» —главный источник правовой информации для профессионалов в сфере юриспруденции
Еженедельная газета «ЮРИДИЧЕСКАЯ ПРАКТИКА» —главный источник правовой информации для профессионалов в сфере юриспруденции Презентация на тему Аркадий Кирсанов в произведение Ивана сергеевича тургенева «отцы и дети»
Презентация на тему Аркадий Кирсанов в произведение Ивана сергеевича тургенева «отцы и дети» Загрязнение окружающей среды.Проблема мусора
Загрязнение окружающей среды.Проблема мусора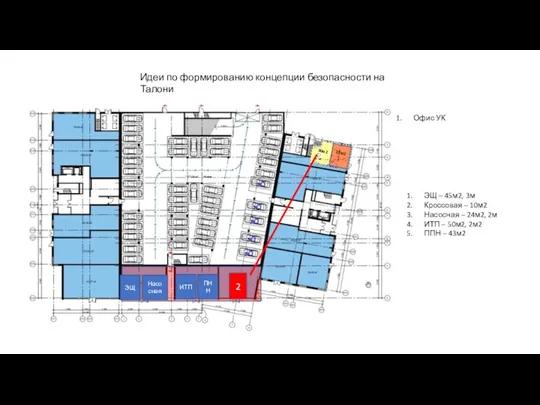 Идеи по формированию концепции безопасности на Талони
Идеи по формированию концепции безопасности на Талони Вводный урок по русскому языку
Вводный урок по русскому языку Апаратты кодтау жне сатау. СРС
Апаратты кодтау жне сатау. СРС Творческий проект "Мой друг Кеша"
Творческий проект "Мой друг Кеша" The Blending of Genres
The Blending of Genres  Программируем в Windows Forms
Программируем в Windows Forms  Биосинтез белков
Биосинтез белков Конструирование балки
Конструирование балки Министерство сельского хозяйства Ульяновской области МЯСНЫЕ ПОРОДЫКРУПНОГО РОГАТОГО СКОТА
Министерство сельского хозяйства Ульяновской области МЯСНЫЕ ПОРОДЫКРУПНОГО РОГАТОГО СКОТА Презентация на тему Нравственный поступок
Презентация на тему Нравственный поступок  1 Descriptive geometry Introduction
1 Descriptive geometry Introduction