Слайд 2АБСОЛЮТНАЯ ВЕЛИЧИНА
В КУРСЕ СРЕДНЕЙ ШКОЛЫ
Существенной характеристикой числа является понятие его абсолютной

величины (модуля). Это понятие имеет широкое распространение в различных разделах физико-математических наук. Поэтому во всех классах, в соответствии с учебной программой следует включать и рассматривать упражнения, содержащие знак абсолютной величины числа.
Слайд 3Одним из определений модуля является
|x| = max {x; -x}

Слайд 4Если x>0, то |x| = max {x; -x} = x
Если x<0, то
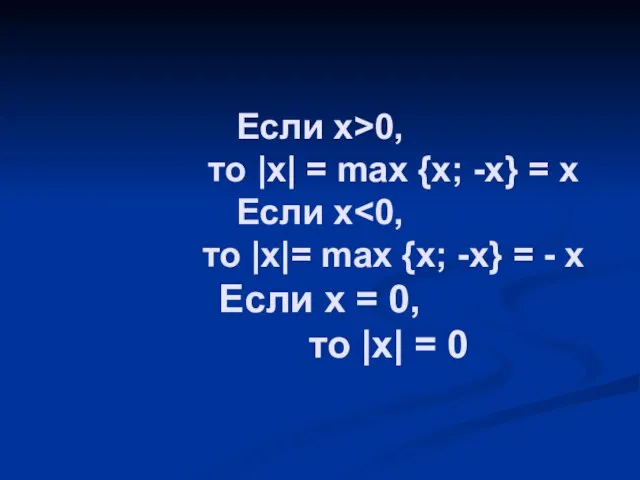
|x|= max {x; -x} = - x
Если x = 0, то |x| = 0
Слайд 5Таким образом,
|x|= x, если x ≥ 0,
- x, если x

< 0.
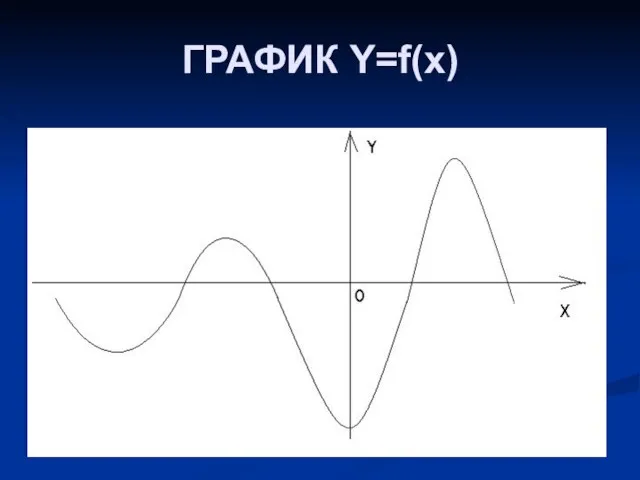
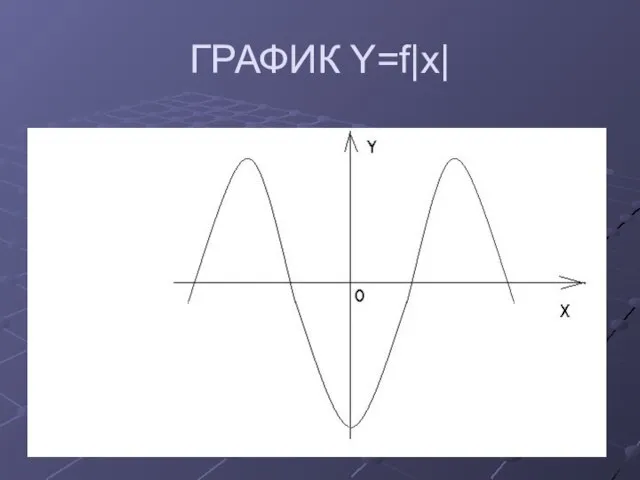
Слайд 6ГРАФИК ФУНКЦИИ y = fIxI.
На основании определения модуля
f(x), если x ≥

0,
y = f(-x), если x < 0.
График этой функции симметричен относительно оси ординат, так как y=f|x| является четной функцией.
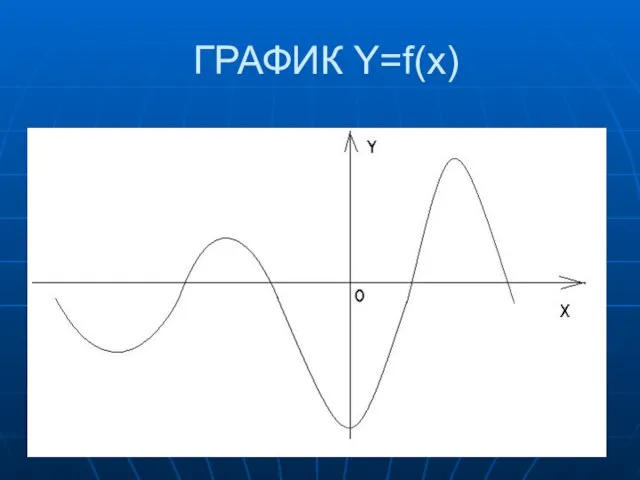
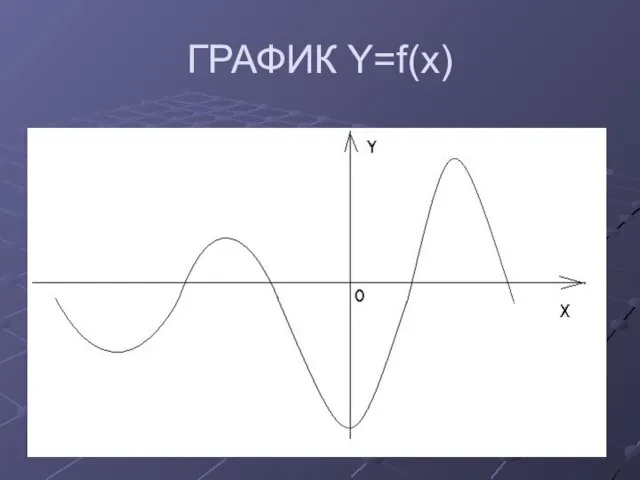
Слайд 7Практическое правило построения функции y = fIxI:
строим график функции y = f(x);
для

X < 0 строим левую часть графика симметрично правой относительно оси ординат.
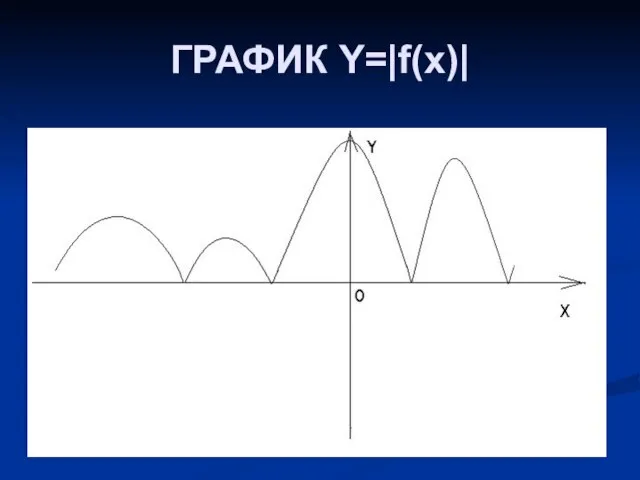
Слайд 10ГРАФИК ФУНКЦИИ y = |f(x)|.
На основании определения модуля
f(x), если f(x) ≥

0,
y = -f(x), если f(x) < 0.
Слайд 11Практическое правило построения функции y = |f(x)|:
строим график функции y = f(x);
на

участках, где график расположен в нижней полуплоскости, то есть где f(x)<0, строим кривые, симметричные построенным относительно оси абсцисс
Слайд 14*
*
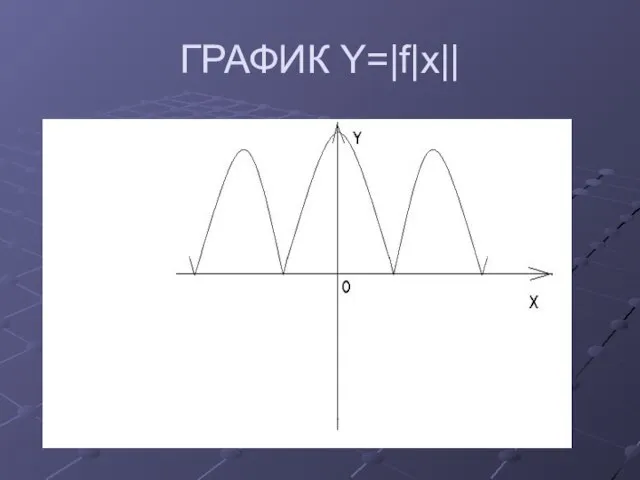
Практическое правило построения функции y = IfIxII:
строим график функции y = f(x);
для

X < 0 строим левую часть графика симметрично правой относительно оси ординат.
участки графика, расположенные в нижней полуплоскости, отображаем на верхнюю симметрично относительно оси абсцисс.
Слайд 18Предлагая эти приемы для построения графиков функции указанного вида, в сознании учащихся

идея геометрических преобразований
(параллельный перенос
и симметрия)
закрепляется, проявляя свои особенности и преимущества.


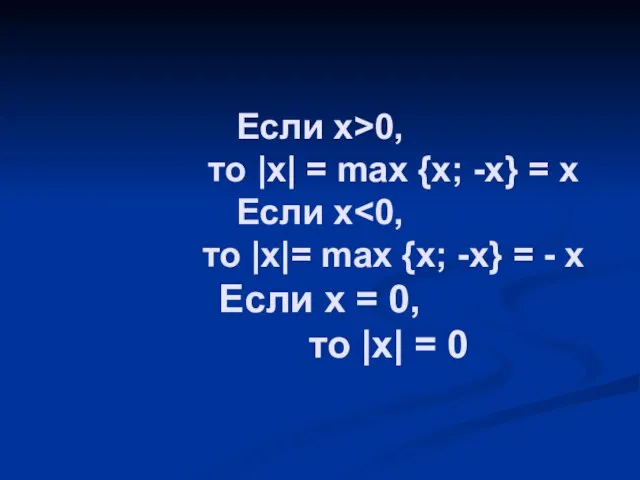







 Алгоритм презентации на защиту
Алгоритм презентации на защиту Современная киноиндустрия
Современная киноиндустрия Кто придумал ноль ?
Кто придумал ноль ? Направления деятельности изостудии Росинка
Направления деятельности изостудии Росинка Объединение Мир искусства. Часть 3
Объединение Мир искусства. Часть 3 Адаптация профессиональных спортсменов к выполнению предусмотренных нагрузок
Адаптация профессиональных спортсменов к выполнению предусмотренных нагрузок es-Persona индивидуальные заказы
es-Persona индивидуальные заказы Основы графической грамоты. Трудовое обучение
Основы графической грамоты. Трудовое обучение Установка разделения изотопов бора методом экстрактивной ректификации
Установка разделения изотопов бора методом экстрактивной ректификации Оценка уровня развития базовых способностей обучающихся
Оценка уровня развития базовых способностей обучающихся Презентация на тему Занятие по профориентации «Профессия - ветеринар»
Презентация на тему Занятие по профориентации «Профессия - ветеринар» История про маленьких лягушат….
История про маленьких лягушат…. Очистка и дезинфекция медицинских инструментов.
Очистка и дезинфекция медицинских инструментов. Особенности кредитно-модульной организации учебного процесса
Особенности кредитно-модульной организации учебного процесса Современные PLC телекоммуникации
Современные PLC телекоммуникации Здоровьесберегающие образовательные технологии на уроках английского языка
Здоровьесберегающие образовательные технологии на уроках английского языка Результаты инновационной работы педагогов ДОУ, представленных в СМИ 2011г.
Результаты инновационной работы педагогов ДОУ, представленных в СМИ 2011г. «Стабильный успех»
«Стабильный успех» Технологические среды в микроэлектронике. Газоподготовка в электронной технике
Технологические среды в микроэлектронике. Газоподготовка в электронной технике Я через 15 лет
Я через 15 лет The Golden Age
The Golden Age Машинные швы
Машинные швы РазработкаГосударственной Стратегии по развитию рынка трудадо 2020 года.
РазработкаГосударственной Стратегии по развитию рынка трудадо 2020 года. Криптосистемы с открытым ключем
Криптосистемы с открытым ключем Экскурсия в город Мастеров и Мастериц
Экскурсия в город Мастеров и Мастериц Битва за Днепр
Битва за Днепр Насилие в произведениях искусства
Насилие в произведениях искусства Страховая Компания «Согласие» является одной из крупнейших отечественных компаний, успешно работающей на Российском рынке страх
Страховая Компания «Согласие» является одной из крупнейших отечественных компаний, успешно работающей на Российском рынке страх