Содержание
- 2. Провоцирующие задачи Задачи на переливание Задачи со спичками Старинные задачи Головоломки Ребусы Cодержание:
- 3. Провоцирующие задачи
- 4. Задачи, условия которых навязывают неверный ответ. Задачи, условия которых подсказывают неверный путь решения. Задачи, вынуждающие придумывать
- 5. 1) Сколько граней имеет новый шестигранный карандаш ? 2) Сколько цифр потребуется, чтобы записать двенадцатизначное число?
- 6. Навязывается ответ – 6, правильный ответ – 8 Навязывается ответ –12, правильный- одной, двумя,3, 4, 5,
- 7. 1) Тройка лошадей проскакала 15 километров. Сколько километров проскакала каждая лошадь? 2) Лупа даёт четырёхкратное увеличение.
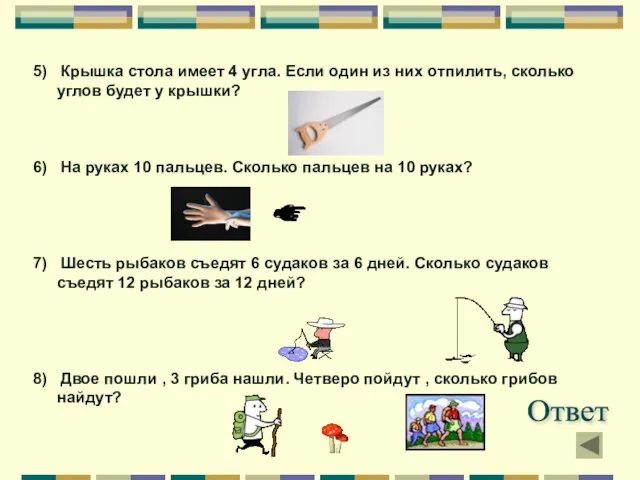
- 8. 5) Крышка стола имеет 4 угла. Если один из них отпилить, сколько углов будет у крышки?
- 9. Ответы: Каждая лошадь проскакала 15 километров. 2. Напрашивается умножение 4*25, но умножать не надо. Ответ 25.
- 10. 1) Построить прямоугольный равнобедренный треугольник, у которого сумма катетов в 2 раза больше гипотенузы . 2)
- 11. Нельзя, так как по условию каждый катет равен гипотенузе. 2. Нельзя, так как любое число, удовлетворяющее
- 12. 4. Задачи, вводящие в заблуждение из-за неоднозначности трактовки терминов Чему равно: 2 в квадрате? 3 в
- 13. Ответы: Прямой Да, можно. Для этого необходимо составить слово Нет, не всегда. На часах после 12
- 14. "Задачи на переливание"
- 15. У нас возник вопрос: "Сколько надо банок и баков чтобы решить задачи?"
- 16. 1) Имеются трехлитровая банка сока и две пустые банки: одна - литровая, другая двухлитровая. Как разлить
- 17. 3 литра 2 литра 1 литр До переливания 3 0 0 После 1 переливания 2 0
- 18. 2) Имеются шестилитровая банка сока и две пустые банки:трех- и четырехлитровая. Как налить 1 литр сока
- 19. одно из решений: 6 литров 4 литра 3 литра До переливания 6 0 0 После 1
- 20. 3) Двое должны разделить поровну 8 ведер кваса, находящегося в восьмиведерном бочонке. Но у них есть
- 21. одно из решений: 8 ведер 5 ведер 3 ведер До переливания 8 0 0 После 1
- 22. Оказывается, бидоны вовсе не нужны, можно, не обливаясь, решить задачу на бумаге... Попробуйте решить и вы...
- 23. Как, пользуясь банками в 3 литра и 5 литров, набрать ровно 1 литр воды? Как отмерить
- 24. решения 1)
- 25. решения 2)
- 26. 3) решения
- 27. Бидон емкостью 10 литров заполнен молоком. Требуется перелить из этого бидона 5 литров в семилитровый бидон,
- 28. решения 4)
- 29. 5) решения
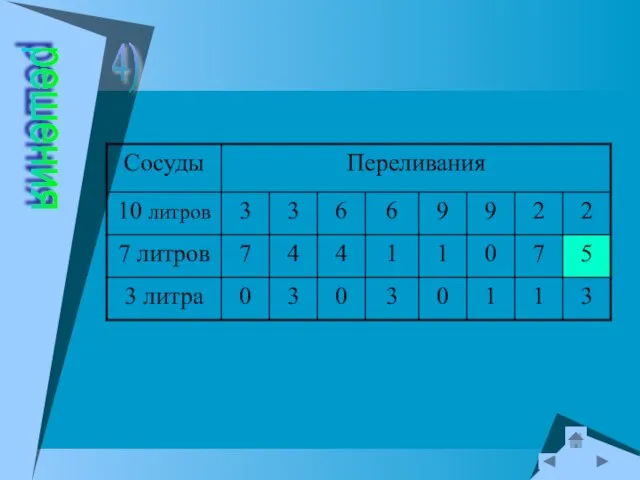
- 30. Десять вёдер кваса Имеются 3 бочонка вместимостью 6 ведер, 3 ведра и 7 ведер. В первом
- 31. решения 6)
- 32. 8) решения
- 33. Задачи со спичками.
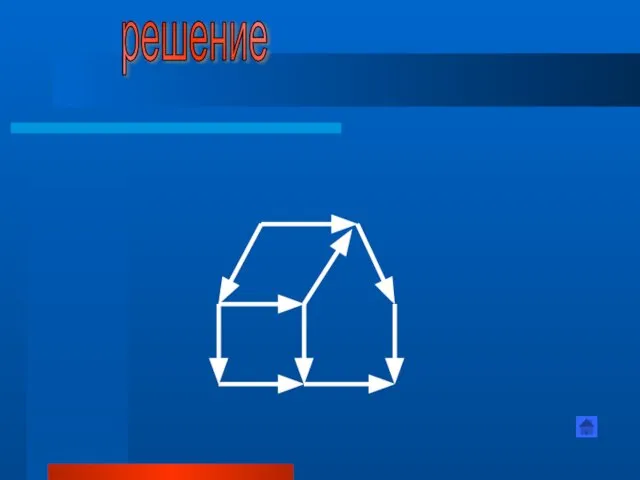
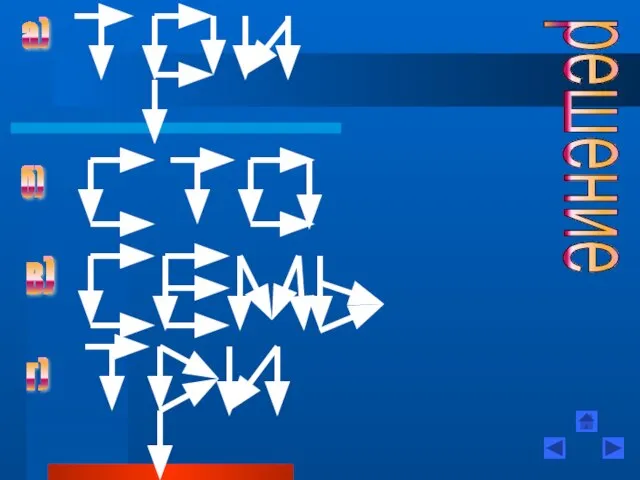
- 34. Из спичек построен дом. Переложите две спички так, чтобы дом повернулся другой стороной. решение
- 35. решение
- 36. Спичечный рак ползет вверх. Переложите три спички так, чтобы он пополз вниз. решение
- 37. решение
- 38. Корова смотрит вправо. Переложите 2 спички, чтобы она смотрела влево решение
- 39. решение
- 40. Переложив 4 спички, превратите топор в три равных треугольника решение
- 41. решение
- 42. можно ли сделать: а) из десяти - три б) из девяти - сто в) из четырнадцати
- 43. а) б) в) г) решение
- 44. Как сделать: а) из трех - один б) из пяти - два в) из пяти -
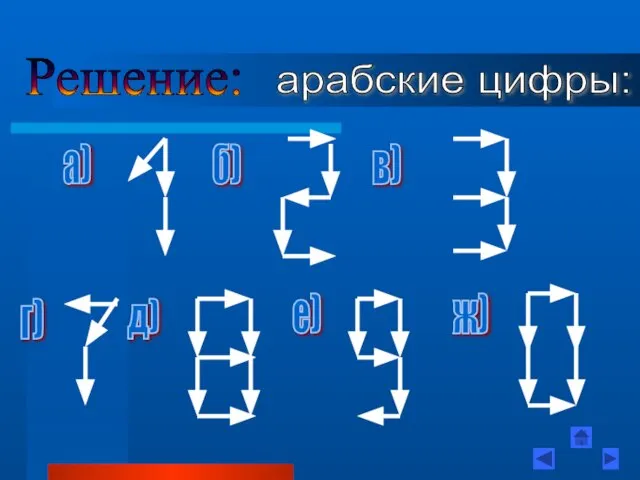
- 45. арабские цифры: Решение: а) б) в) г) д) е) ж)
- 46. Сумеете ли вы сделать: а)из двух - пять б)из двух - десять в)из четырех - пять
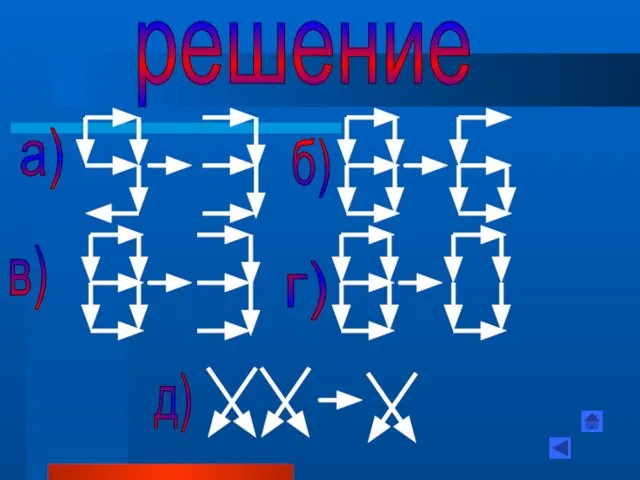
- 47. решение а) б) в) г) д)
- 48. Может ли такое быть: а)девять без одного - три б)восемь без одного - шесть в)восемь без
- 49. решение а) б) в) г) д)
- 50. старинные задачи
- 51. Летела стая гусей, а навстречу им летит один гусь и говорит: Здравствуйте, сто гусей! Нас не
- 52. Пусть столько будет Х, полстолька – Х/2, четверть столька – Х/4, получаем уравнение: Х+X+Х/2+X/4+1=100 4Х+4Х+2Х+Х=99·4 11Х=99·4
- 53. 2. Шел мужик в Москву и повстречал 7 богомолок, у каждой из них было по мешку,
- 54. Бедный мужик один шагал в Москву, а богомолки шли ему навстречу. Решение
- 55. 3. В 336- ведерное хранилище всякие 2 часа одною трубою втекает воды 70 ведер(1 ведро-12,3 л.),
- 56. Каждые 2 часа остается в водохранилище 70-42=28 ведер Понадобится 336:28=12раз 12·2=24 часа Ответ: наполнится за 24
- 57. 4. Вол съел копну одним часом, а конь съел копну в два часа, а коза съела
- 58. За 12 часов вол съест 12 копен, конь – 6, коза – 4, всего 22 копны.
- 59. Решите сами Юноша некий пошел с Москвы к Вологде и идет на всякий день по 40
- 60. ответы В 8 дней, За 15 минут, За 35 дней, Кроликов – 12, фазанов 23.
- 61. танграм головоломки колумбово яйцо
- 62. Из листа картона квадратной формы вырежьте детали головоломки «танграм»
- 63. попробуйте сложить из частей "танграма" данные фигуры
- 64. попробуйте сложить из частей "танграма" данные фигуры
- 65. "колумбово яйцо" попробуйте сложить из частей "колумбова яйца" данные фигуры решения
- 66. подсказка для тех, кто не смог решить
- 67. ребусы
- 69. К Вот ребусы, составленные с помощью этих приемов, попробуйте прочитать эти слова. К О А Б
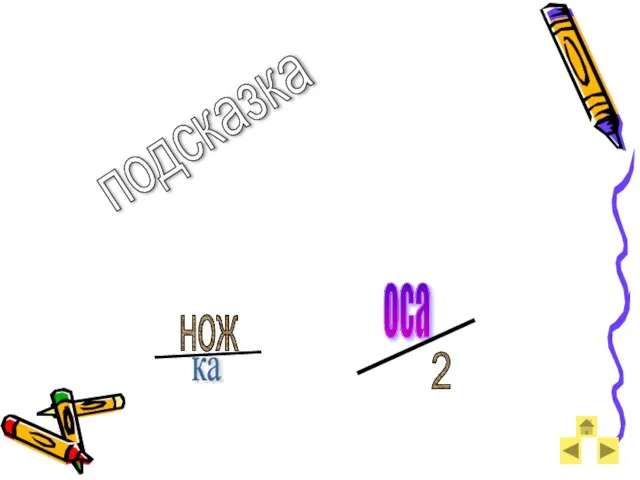
- 70. ка оса 2 нож подсказка
- 71. Полуподвал подкова бук пора Порт изба изба сад подсказка
- 73. защелка
- 74. родина
- 75. наклонная
- 76. два
- 77. диаметр
- 78. высота
- 80. апофема
- 81. числитель
- 82. задача
- 83. диагональ
- 84. отрезок
- 85. Источники: 1. Труднев В.П. «Считай, смекай, отгадывай», С-Петербург, 1997 год. 2. Ц. Даширобданова «Творческое задание на
- 87. Скачать презентацию













































































 «Обзор законодательства Республики Казахстан в сфере социальной поддержки и обеспечения социальными услугами»
«Обзор законодательства Республики Казахстан в сфере социальной поддержки и обеспечения социальными услугами» Роспись петуха по мотивам Филимоновской росписи
Роспись петуха по мотивам Филимоновской росписи Гражданское право. Понятие и виды сроков в гражданском праве
Гражданское право. Понятие и виды сроков в гражданском праве Модернизм
Модернизм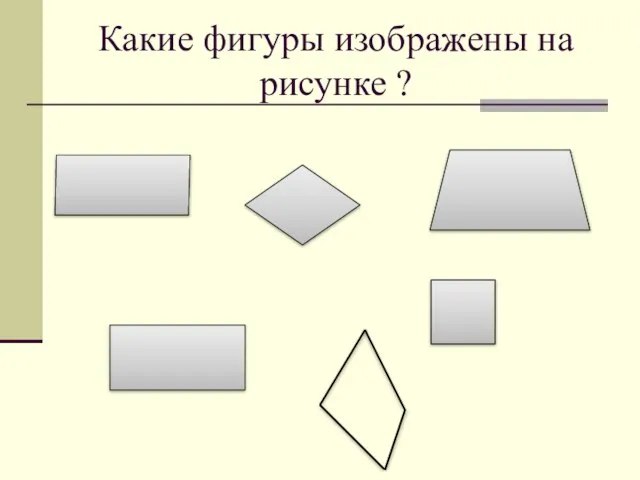 Какие фигуры изображены на рисунке ?
Какие фигуры изображены на рисунке ? Перенос слова переносятся по слогам
Перенос слова переносятся по слогам Принтеры
Принтеры Методическая разработка «Создание презентаций» Элективный курс для 10 класса.
Методическая разработка «Создание презентаций» Элективный курс для 10 класса. Вейк-лебедка - летний бизнес. Вейкпарк в пляжной зоне
Вейк-лебедка - летний бизнес. Вейкпарк в пляжной зоне Федеральное Собрание РФ
Федеральное Собрание РФ Инжиниринг нефтехимии и нефтегазопереработки
Инжиниринг нефтехимии и нефтегазопереработки Китайский клуб МИИТа
Китайский клуб МИИТа Мой город, с тебя начинается Родина (город Сатка)
Мой город, с тебя начинается Родина (город Сатка) Спартакиада пенсионеров муниципального образования Город Гатчина
Спартакиада пенсионеров муниципального образования Город Гатчина Эры. Основные события органического мира
Эры. Основные события органического мира Презентация на тему Операционные системы на мобильных устройствах
Презентация на тему Операционные системы на мобильных устройствах  Живопись
Живопись Михайленко Юлия Борисовна учитель начальных классов ГБОУ гимназии № 1518 г. Москвы
Михайленко Юлия Борисовна учитель начальных классов ГБОУ гимназии № 1518 г. Москвы Муниципальное общеобразовательное учреждение лингвистическая гимназия № 70
Муниципальное общеобразовательное учреждение лингвистическая гимназия № 70 МОСКВА- ГОРОД ГЕРОЙ . Битва за Москву(30 сентября 1941- 20 апреля 1942)
МОСКВА- ГОРОД ГЕРОЙ . Битва за Москву(30 сентября 1941- 20 апреля 1942) Векторы в пространстве и не только
Векторы в пространстве и не только Презентация на тему История развития отечественной вычислительной техники
Презентация на тему История развития отечественной вычислительной техники Трансформация изображения через трансформацию формы - серия открыток
Трансформация изображения через трансформацию формы - серия открыток ОРНАМЕНТЫ в национальном костюме
ОРНАМЕНТЫ в национальном костюме Цветник для солнечного места “Степной бриз ”
Цветник для солнечного места “Степной бриз ” Презентация на тему Тургенев. Стихи в прозе
Презентация на тему Тургенев. Стихи в прозе 287 Воскресшему служу я
287 Воскресшему служу я Берлину заменить Северный поток-2 другим проектом
Берлину заменить Северный поток-2 другим проектом