Вписанная окружность

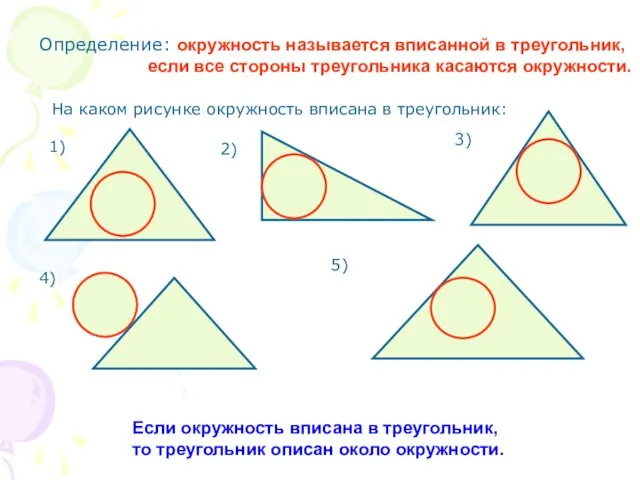
Определение: окружность называется вписанной в треугольник,
если все стороны треугольника касаются окружности.
Если окружность вписана в треугольник,
то треугольник описан около окружности.

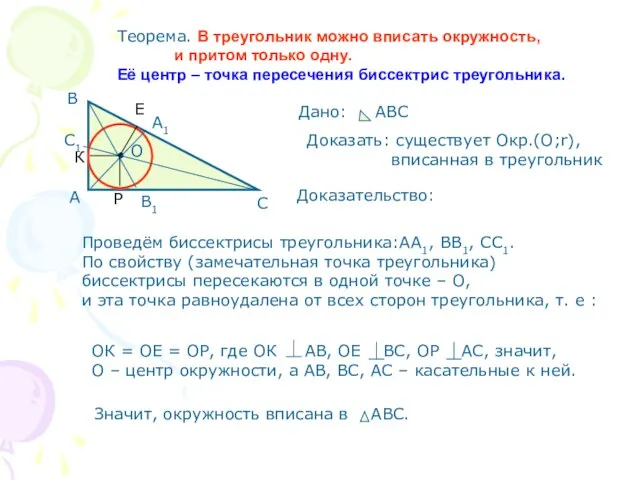
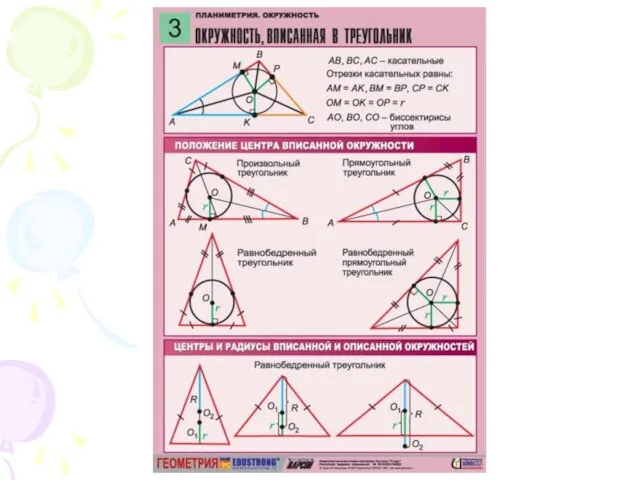
Теорема. В треугольник можно вписать окружность,
и притом только одну.
Её центр – точка пересечения биссектрис треугольника.
Доказать: существует Окр.(О;r),
вписанная в треугольник
Доказательство:
Проведём биссектрисы треугольника:АА1, ВВ1, СС1.
По свойству (замечательная точка треугольника)
биссектрисы пересекаются в одной точке – О,
и эта точка равноудалена от всех сторон треугольника, т. е :

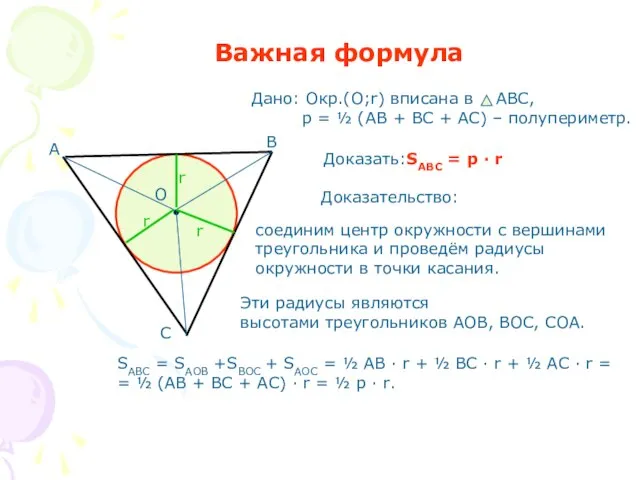
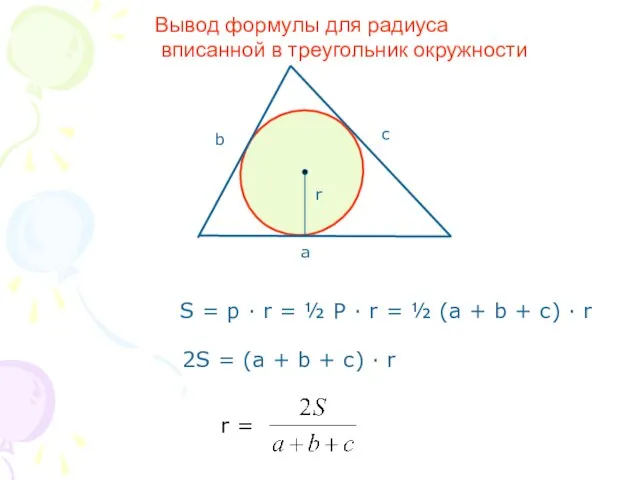
Важная формула
Доказать:SABC = p · r
Доказательство:
Эти радиусы являются
высотами треугольников АОВ, ВОС, СОА.
соединим центр окружности с вершинами
треугольника и проведём радиусы
окружности в точки касания.
SABC = SAOB +SBOC + SAOC = ½ AB · r + ½ BC · r + ½ AC · r =
= ½ (AB + BC + AC) · r = ½ p · r.

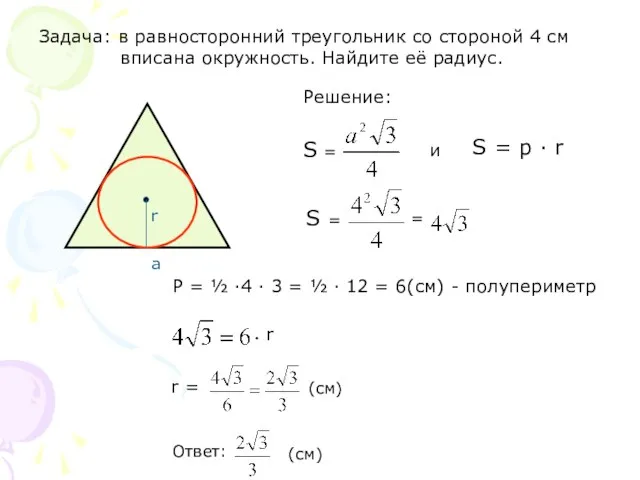
Задача: в равносторонний треугольник со стороной 4 см
вписана окружность. Найдите её радиус.
P = ½ ·4 · 3 = ½ · 12 = 6(см) - полупериметр
Решение:

S = p · r = ½ P · r = ½ (a + b + c) · r
2S = (a + b + c) · r
Вывод формулы для радиуса
вписанной в треугольник окружности

Задача: в прямоугольный треугольник вписана окружность,
гипотенуза точкой касания делится на отрезки 6 см и 4 см.
Найдите радиус вписанной окружности.
Решение:
АВ = АМ + ВМ = 6 + 4 = 10(см)
По теореме Пифагора: АС2 + ВС2 = АВ2
,
АС= 6+ r, ВС = 4 + r
(6 + r)2 + (4 + r)2 = 102
Решив квадратное уравнение, получим r = 2 см
Ответ: 2 см

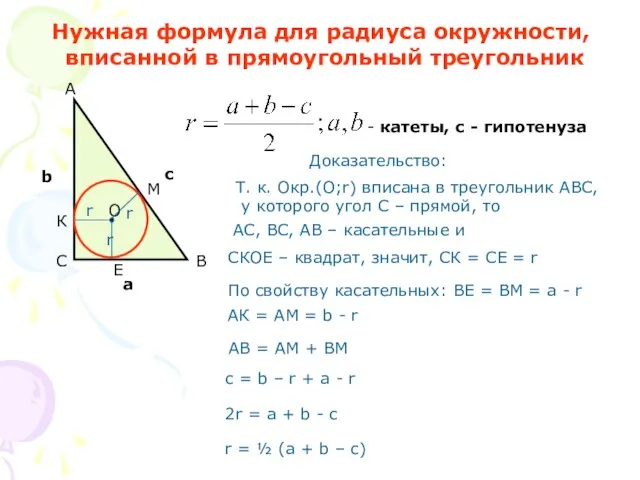
Нужная формула для радиуса окружности,
вписанной в прямоугольный треугольник
Доказательство:
СКОЕ – квадрат, значит, СК = СЕ = r
По свойству касательных: ВЕ = ВМ = а - r
АК = АМ = b - r
AB = AM + BM
c = b – r + a - r
2r = a + b - c
r = ½ (a + b – c)
Т. к. Окр.(О;r) вписана в треугольник АВС,
у которого угол С – прямой, то
АС, ВС, АВ – касательные и

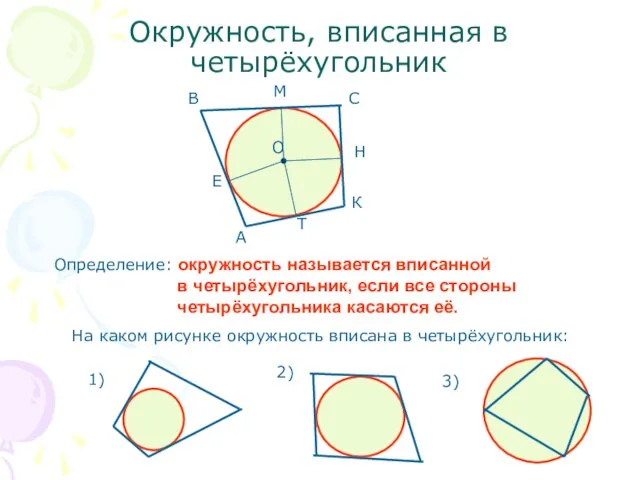
Окружность, вписанная в четырёхугольник
Определение: окружность называется вписанной
в четырёхугольник, если все стороны четырёхугольника касаются её.

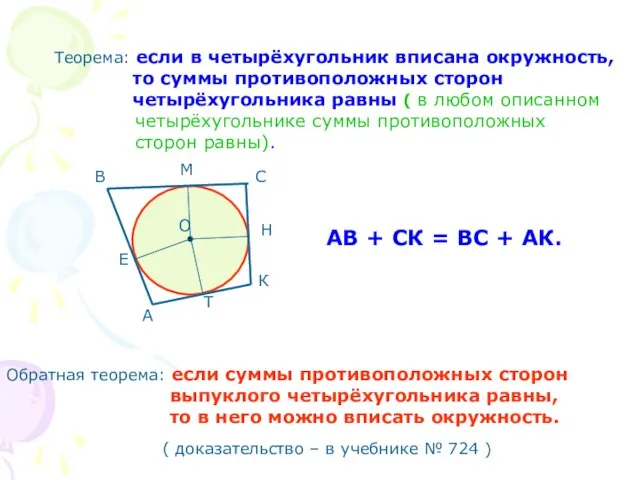
Теорема: если в четырёхугольник вписана окружность,
то суммы противоположных сторон
четырёхугольника равны ( в любом описанном
четырёхугольнике суммы противоположных
сторон равны).
Обратная теорема: если суммы противоположных сторон
выпуклого четырёхугольника равны,
то в него можно вписать окружность.
АВ + СК = ВС + АК.
( доказательство – в учебнике № 724 )

Задача: в ромб, острый угол которого 600, вписана окружность,
радиус которой равен 2 см. Найти периметр ромба.
Решение: