Слайд 2Временной (динамический) ряд – это ряд последовательно расположенных во времени числовых значений

соответствующего показателя
Элементы временного ряда:
уровни ряда (yt)- числовые значения того или иного показателя;
время (t).
Виды временных рядов:
моментные, если время задано моментами;
интервальные, если время задано интервалами.
Слайд 3Модели на основе рядов динамики
Модели изолированного динамического ряда.
Модели системы взаимосвязанных рядов динамики.
Модели

авторегрессии.
Модели с распределенным лагом.
Слайд 4Компоненты временного ряда
Тенденция (T)
Периодические колебания (P)
Случайные колебания (E)

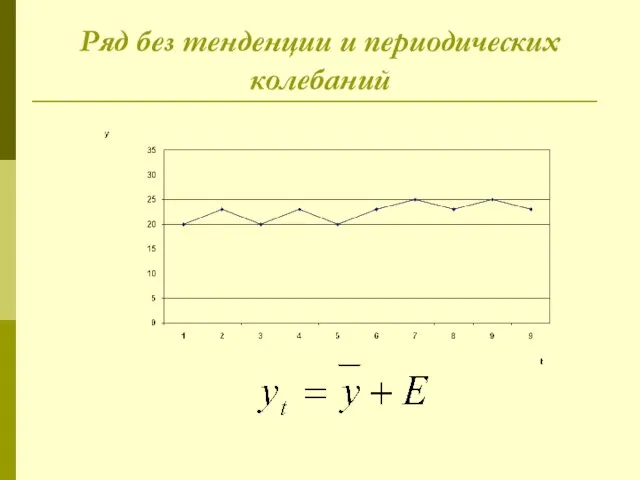
Слайд 5Ряд без тенденции и периодических колебаний
Слайд 7
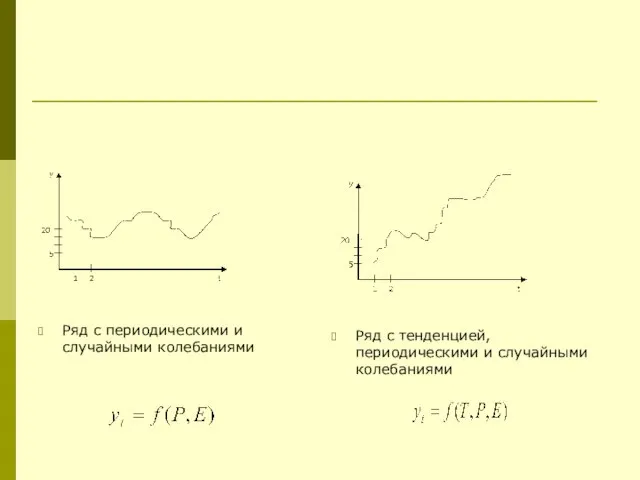
Ряд с периодическими и случайными колебаниями
Ряд с тенденцией, периодическими и случайными колебаниями
Слайд 8Аддитивная модель
Мультипликативная модель

Слайд 9Автокорреляция уровней ряда и ее последствия
Корреляционная зависимость между последовательными значениями уровней временного

ряда называется автокорреляцией уровней ряда
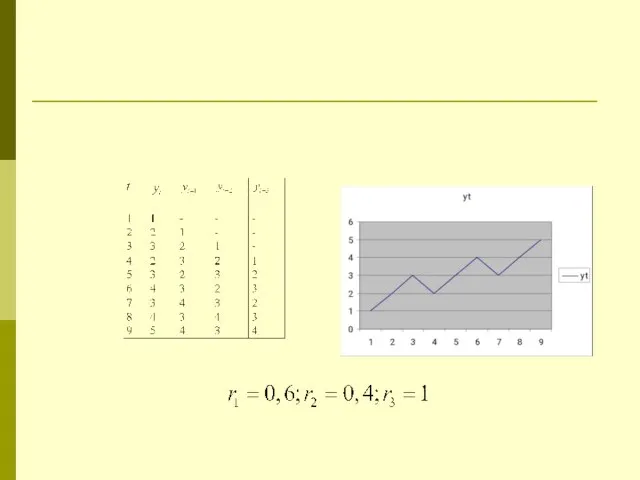
Слайд 11Пример
Имеются данные о расходах на конечное потребление и уровне дохода за 7
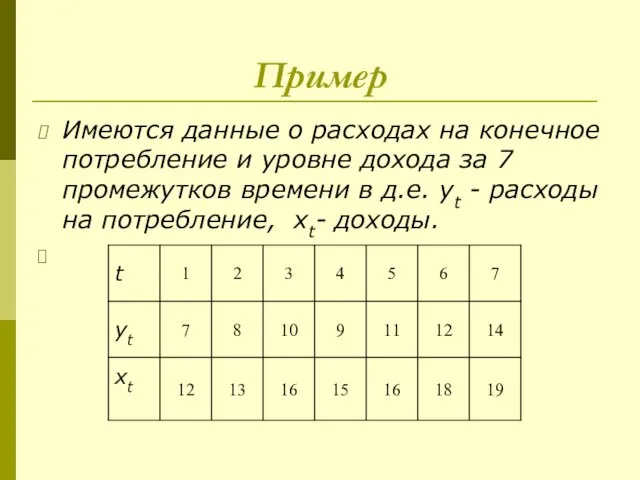
промежутков времени в д.е. yt - расходы на потребление, xt- доходы.
Слайд 14Моделирование тенденций временного ряда
Метод аналитического выравнивания сводится к замене фактических данных

сглаженными, определенными по выбранной математической функции. При этом, уровни временного ряда рассматриваются как функция от времени:
Слайд 15Этапы построения модели тенденции (уравнения тренда)
Выбор математической функции, описывающей тенденцию
Оценка параметров

модели
Проверка адекватности выбранной функции и оценка точности модели
Расчет точечного и интервального прогнозов
Слайд 16Виды математических функций, описывающих тенденцию
Функции с монотонным характером возрастания (убывания) и отсутствием

пределов роста (снижения)
Кривые с насыщением, т. е. устанавливается нижняя или верхняя граница изменения уровней ряда
S-образные кривые, т. е. кривые с насыщением, имеющие точку перегиба







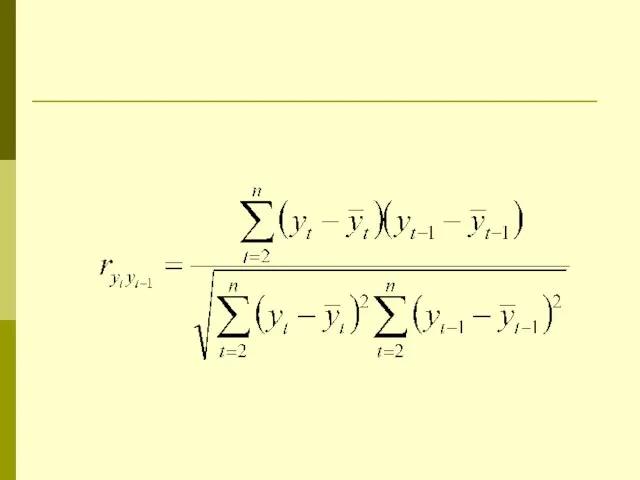







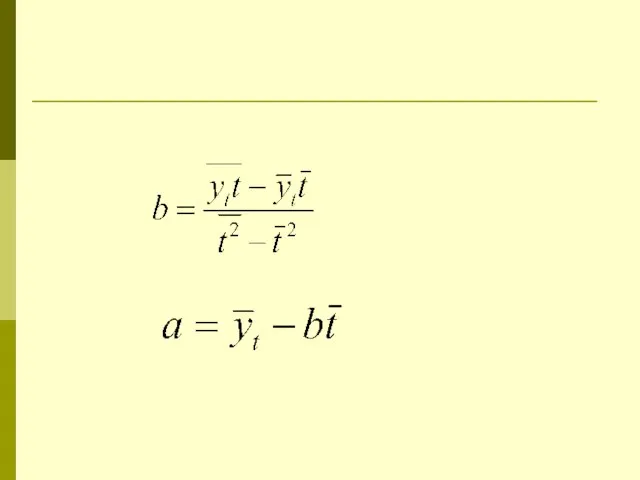
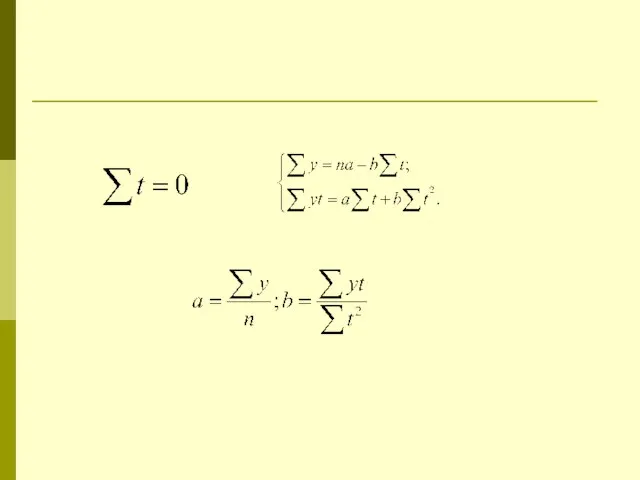

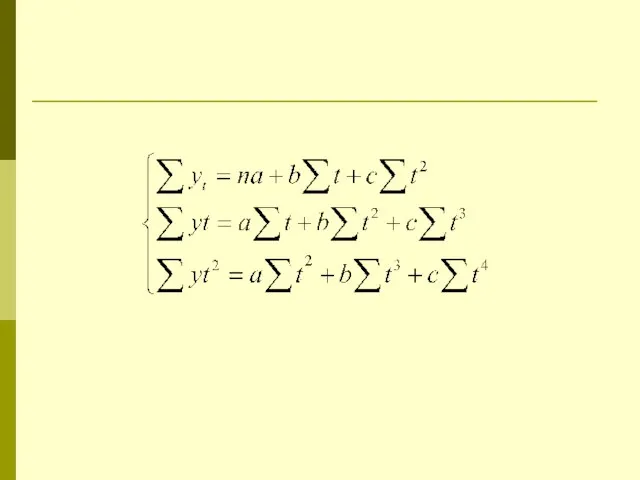

 Обеспечение непрерывного IT-образования в школе и вузе в условиях перехода на образовательные стандарты нового поколения
Обеспечение непрерывного IT-образования в школе и вузе в условиях перехода на образовательные стандарты нового поколения РОЛЬ СПЕЦИАЛЬНЫХ ЗНАНИЙ В ОБЛАСТИ ПСИХИАТРИИ И ПСИХОЛОГИИ В РАЗВИТИИ ЮВЕНАЛЬНОЙ ЮСТИЦИИ Е.И. Цымбал
РОЛЬ СПЕЦИАЛЬНЫХ ЗНАНИЙ В ОБЛАСТИ ПСИХИАТРИИ И ПСИХОЛОГИИ В РАЗВИТИИ ЮВЕНАЛЬНОЙ ЮСТИЦИИ Е.И. Цымбал Процессоры ADSP-BF53
Процессоры ADSP-BF53 Жизнь и творчество Виктора Михайловича Васнецова
Жизнь и творчество Виктора Михайловича Васнецова Все о полиграфическом рынке
Все о полиграфическом рынке История Голливуда и независимого кино
История Голливуда и независимого кино Зачем людям имена
Зачем людям имена ООО «ФЛЭР ИНЖИНИРИНГ»
ООО «ФЛЭР ИНЖИНИРИНГ» Презентация отряда имени В.Куриленко
Презентация отряда имени В.Куриленко Презентация на тему Мамин Сибиряк
Презентация на тему Мамин Сибиряк Проблемы и возможности борьбы с фальсифицированными продуктами/скрининг лекарственных средств
Проблемы и возможности борьбы с фальсифицированными продуктами/скрининг лекарственных средств Гипертекстовая интерпретация отрывка из оды М.В. Ломоносова
Гипертекстовая интерпретация отрывка из оды М.В. Ломоносова Colección de Barbies
Colección de Barbies Искусство Гжели
Искусство Гжели Презентация на тему Эрнест Резерфорд
Презентация на тему Эрнест Резерфорд Презентация на тему Польша
Презентация на тему Польша Автобус Wubbo Superbus (ОАЭ)
Автобус Wubbo Superbus (ОАЭ) Презентация на тему Скульптура Древнего Рима
Презентация на тему Скульптура Древнего Рима  Видоизмененные побеги
Видоизмененные побеги ПОДБОР ВЫСОКОКВАЛИФИЦИРОВАННОГО ПЕРСОНАЛА
ПОДБОР ВЫСОКОКВАЛИФИЦИРОВАННОГО ПЕРСОНАЛА Презентация на тему Биотопы суши
Презентация на тему Биотопы суши Презентация на тему История развития отечественной вычислительной техники
Презентация на тему История развития отечественной вычислительной техники БИЗНЕС: ПОИСК ИДЕИ
БИЗНЕС: ПОИСК ИДЕИ Die Muscheln
Die Muscheln Актуализация грамматического материала при интенсивной подготовке к ГИА
Актуализация грамматического материала при интенсивной подготовке к ГИА Логика
Логика УСТРОЙСТВО РИМСКОЙ РЕСПУБЛИКИ
УСТРОЙСТВО РИМСКОЙ РЕСПУБЛИКИ Организация производственного процесса
Организация производственного процесса