Содержание
- 2. При аппроксимации функций, а также в некоторых других задачах приходится вычислять значения многочленов вида При непосредственном
- 3. Теорема Безу Остаток от деления многочлена на двучлен равен значению этого многочлена при Доказательство: , где
- 4. Рассмотрим более простой метод деления многочлена на линейный двучлен Представим многочлен в виде , где или
- 5. Раскрывая скобки в последнем равенстве имеем После приведения подобных членов имеем
- 6. Приравнивая коэффициенты при одинаковых степенях получим равенства или
- 7. Вычисления удобно располагать по следующей схеме (называемой схемой Горнера): Этот метод требует n умножений и n
- 8. Вычисление значений аналитической функции
- 9. Действительная функция f(x) называется аналитической в точке если в некоторой окрестности этой точки функция разлагается в
- 10. Разность называется остаточным членом и представляет собой ошибку при замене функции f(x) полиномом Тейлора
- 11. Как известно, где В частности, для ряда Маклорена имеем где Имеются также другие формы остаточных членов.
- 12. Вычисление значений показательной функции Для показательной функции справедливо разложение Остаточный член ряда имеет вид
- 13. Приближенное вычисление для малых x удобно вести , пользуясь следующей рекуррентной записью: (k = 1, 2,
- 14. Для остатка ряда может быть получена следующая оценка: при Поэтому процесс суммирования может быть прекращен, как
- 15. Вычисление значений логарифмической функции Пользуемся разложением по степеням Пусть x – положительное число. Представим его в
- 16. Тогда, полагая , получим где
- 17. Обозначив получаем рекуррентную запись , Процесс суммирования прекращается, как только выполнится неравенство где – допустимая погрешность.
- 18. Вычисление значений синуса и косинуса. Для вычисления значений функций и пользуемся степенными разложениями
- 19. Эти ряды при больших x сходятся медленно, но, учитывая периодичность функции и и формулы приведения тригонометрических
- 20. При этом можно использовать следующие рекуррентные формулы:
- 21. Так как в промежутке ряд знакочередующийся с монотонно убывающими по модулю членами, то для его остатка
- 23. Скачать презентацию




















 Олимпийские игры в Греции 5 класс
Олимпийские игры в Греции 5 класс Поколение ЭВМ
Поколение ЭВМ ИКТ в системе работы с одаренными детьми
ИКТ в системе работы с одаренными детьми Histoire de Disneyland Paris
Histoire de Disneyland Paris Химическая связь
Химическая связь Вещное право в МЧП. Тема 8
Вещное право в МЧП. Тема 8 Где получить профессию финансиста?
Где получить профессию финансиста?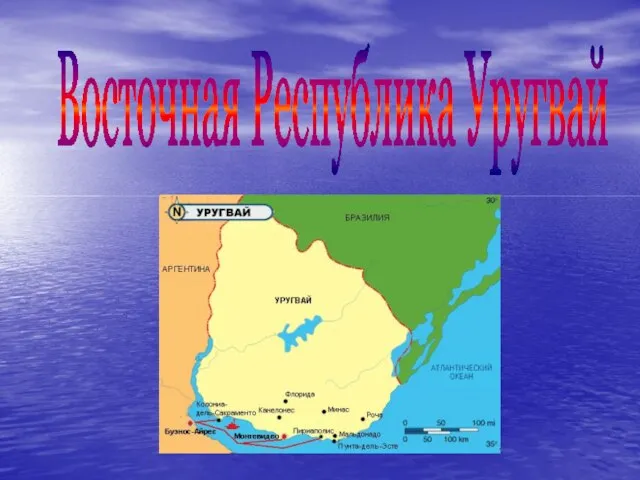 Презентация на тему Уругвай
Презентация на тему Уругвай Презентация без названия
Презентация без названия Модели данных
Модели данных  Письмо заглавной буквы Ж
Письмо заглавной буквы Ж Повторение изученного
Повторение изученного Музеи искусства. Картина-пейзаж
Музеи искусства. Картина-пейзаж Две стратегии повышения эффективности контекстной рекламы Андрей Лебедев , Зураб Полосин, интернет-маркетологи департамента Ин
Две стратегии повышения эффективности контекстной рекламы Андрей Лебедев , Зураб Полосин, интернет-маркетологи департамента Ин Презентация на тему Социальный прогресс и развитие общества 8 КЛАСС
Презентация на тему Социальный прогресс и развитие общества 8 КЛАСС Презентация на тему Причастие как часть речи (7 класс)
Презентация на тему Причастие как часть речи (7 класс) Деньги Money
Деньги Money Презентация на тему Начало Реформации в Европе
Презентация на тему Начало Реформации в Европе  Презентация на тему Архитектура классицизма в России МХК 11 класс
Презентация на тему Архитектура классицизма в России МХК 11 класс  Налогообложение и социальная политика РФ.
Налогообложение и социальная политика РФ. Групповая дифференциация и лидерство
Групповая дифференциация и лидерство Теория цвета
Теория цвета Гуморальная регуляция автономных функций
Гуморальная регуляция автономных функций Презентація
Презентація Порахуй з Вовком!
Порахуй з Вовком! Производство Наноструктурированного пенобетона
Производство Наноструктурированного пенобетона Система защиты труб от замерзания
Система защиты труб от замерзания Презентация на тему Развитие связной речи у дошкольников Советы родителям
Презентация на тему Развитие связной речи у дошкольников Советы родителям