Ймовірнісне моделювання. Метод статистичних випробувань

Суть методу полягає в тому, що замість опису випадкових явищ аналітичними залежностями проводиться розіграш випадкового явища за допомогою деякої процедури, яка дає випадковий результат.
За допомогою розіграшу отримують одну реалізацію випадкового явища.
Здійснюючи багаторазово такий розіграш, накопичують статистичний матеріал (множина реалізацій випадкової величини), який можна обробляти статистичними методами.
Розглянемо на прикладах.

Вирішимо цю задачу методом статистичних випробувань.
Процедуру розіграшу реалізуємо підкиданням одночасно чотирьох монет.
Якщо монета падає лицьовою стороною, то вважаємо, що стрілок влучив у ціль. Позначимо через m число успішних випробувань.
Зробимо N випробувань, тоді відповідно до теореми Бернуллі
Рймов = m/N
У разі значного збільшення числа випробувань N частота ураження цілі буде збігатися з ймовірністю
рймов = 0.6875.

Приклад 2. Нехай є деяка ціль, на яку бомбардувальники скидають n бомб.
Кожна бомба вражає область у вигляді кола радіусом r (рис.).
Ціль вважається ураженою, якщо одночасно бомбами накрите К відсотків площі S.
Знайти ймовірність ураження цілі.
Аналітично вирішити цю задачу дуже важко.
Покажемо, як її можна вирішити методом статистичних випробувань.

Накладемо координатну сітку на всю можливу область попадання бомб.
Розіграємо n точок - координат попадання бомб.
Наведемо біля кожної точки коло радіусом r (рис.) і визначимо заштриховану площу ураження.
Якщо заштрихована площа становитиме К відсотків і більше всієї площі цілі S, то ціль вважається ураженою, а випробування успішним.
В іншому випадку ціль не буде вражена і випробування не успішне.

Алгоритм методу статистичних випробувань такий:
1. Визначити, що собою являтиме випробування або розіграш.
2. Визначити, яке випробування є успішним, а яке - ні.
3. Провести велику кількість випробувань.
4. Обробити отримані результати статистичними методами і розрахувати статистичні оцінки шуканих величин.

До недоліків методу можна віднести необхідність проведення великої кількості випробувань, щоб отримати результат з заданою точністю.
Таким чином, метод статистичних випробувань - це метод математичного моделювання випадкових величин, в якому сама випадковість безпосередньо включена в процес моделювання і є його важливим елементом.
Кожен раз, коли в хід виконання деякої операції втручається випадковий фактор, його вплив моделюється за допомогою розіграшу.

Для ефективного розіграшу випадкових величин використовують генератори випадкових чисел.
Такі генератори будуються апаратними та програмними методами.
Апаратні методи генерування випадкових величин базуються на використанні деяких фізичних явищ (шумів електронних пристроїв, радіоактивного випромінювання).
Під час використання апаратних генераторів випадковий електричний сигнал перетворюється в двійковий код, який вводиться в комп'ютер за допомогою аналогово-цифрових перетворювачів.

Один з найбільш поширених способів - використання шумів електронних пристроїв.
Якщо на підсилювач не подавати ніякий сигнал і включити його на повну потужність, то буде чутно шипіння (шум).
Цей безперервний сигнал можна перетворити в дискретний.
У більшості випадків його підсилюють і встановлюють граничне значення напруги шумового сигналу, перевищення якого можна вважати значенням двійковій одиниці на деякому малому проміжку часу t, в протилежному випадку отримуємо двійковий нуль.

Найбільш поширеними на практиці є програмні генератори.
Вони повинні відповідати таким вимогам:
генерувати статистично незалежні випадкові числа, рівномірно розподілені в інтервалі [0,1];
мати можливість відтворювати задані послідовності випадкових чисел;
витрати ресурсів процесора на роботу генератора повинні бути мінімальними;
легко створювати незалежні послідовності випадкових чисел (потоки).

Лінійні конгруентні генератори.
У більшості сучасних програмних генераторів використовується властивість конгруентності, яке полягає в тому, що два цілих числа А і В є конгруентними за модулем m, якщо їх різниця (А-В) є число, яке ділиться на m без залишку.
Записується це так:
A = B (mod m)

Зазвичай використовується лінійний мультиплікативний конгруентний метод, рекурентне співвідношення для якого має вигляд
де a та m – деякі константи.
Необхідно взяти останнє випадкове число Xi, помножити його на постійний коефіцієнт a і взяти модуль отриманого числа по m, тобто розділити на m і отримати залишок.
Цей залишок і буде наступним псевдовипадковим числом Xi.

Одержані за формулою значення Хi належать діапазону 0≤ Хi ≤ m-1 і мають рівномірний дискретний розподіл.
Щоб отримати випадкове значення з інтервалу [0,1], треба Хi розділити на m.
Для двоїчного комп’ютера m =2g -1, де g – довжина розрядної сітки.
Наприклад, для 32-роз­рядного комп’ютера m = 231 – 1 = 2147483647, оскільки один розряд задає знак числа.

У мові GPSS World використовується мультиплікативний конгруентний алгоритм Лемера з максимальним періодом, який генерує 2147483647 унікальних випадкових чисел без повторення.
Ці числа генерують спеціальні генератори, які позначаються RN <№>, де № - номер генератора випадкових чисел (може приймати значення від 1 до 7).
Під час відвідування таких генераторів видаються цілі випадкові числа в діапазоні від 0 до 999 включно.
При використанні генераторів в випадкових функціях розподілів випадкові числа генеруються в діапазоні від 0 до 0,999999 включно.

Перевірка послідовностей випадкових чисел.
Статистичні властивості всіх послідовностей випадкових чисел потрібно перевіряти.
Для цього використовують критерії. Найбільш часто використовують такі критерії (тести):
Частотний - з використанням критерію Колмогорова-Смирнова або критерію χ2;
Автокореляційний – з вимірюванням кореляції між Хi и Хi+k , де k – зсув по послідовності (k = 1,2…);
Серіальний – з фіксацією частоти появи всіх можливих комбінацій чисел і виконанням оцінювання по критерію χ2;
Циклічний – з перевіркою кількості циклів більше і менше деякої константи.

Моделювання дискретних випадкових величин.
Моделювання подій. Нехай необхідно змоделювати появу деякої події А, ймовірність настання якої дорівнює Р(А)=Р.
Позначимо звертання до генератора, який розігрує випадкові, рівномірно розподілені на інтервалі (0, 1) числа ri, через R.
Подія А при розіграші будет наставати тоді, коли ri ≤ Р (рис.), а якщо ri > Р , то відбувається подія Ā.

Дійсно, якщо f(r) – функція густини рівномірно розподіленої випадкової величини r, то
Даний метод використовується в мові GPSS для блока TRANSFER в статистичному режимі роботи.

Моделювання групи несумісних подій.
Нехай є група несумісних подій, А1, А2, ..,. Аk.
Відомі ймовірності настання подій Р(А1), Р(А2), ..., Р(Аk).
Тоді через несумісність випробувань
Нехай pi = Р(Аi), р0 = 0. На відрізку (0, 1) відкладемо ці ймовірності (рис.).

Якщо одержане число потрапило в інтервал від до , то відбулася подія
Аi.
Таку процедуру називають визначенням ре­зультату випробування по жеребу, і вона
ґрунтується на формулі
, де р0 = 0.

Моделювання умовної події.
Моделювання умовної події А, яке відбувається за умови, що настає подія В з ймовірністю Р (А / В), показано на рис.
Спочатку моделюємо подію В.
Якщо подія В відбувається, то моделюємо настання події А, якщо ж подія В не відбувається, то не моделюємо настання події А.

Моделювання випадкової дискретної величини.
Моделювання випадкової дискретної величини виконується аналогічно моделюванню групи несумісних подій.
Дискретна випадкова величина X задається відповідно до таблиці, в якій вказані можливе значення величини і її ймовірність.
Випадкову величину X можна уявити як повну групу подій:
А1 = (Х = х1), А2 = (Х = х2), …, Аn = (Х = хn).
Даний метод використовується в мові GPSS для моделювання дискретних випадкових функцій розподілу.

Геометричний розподіл.
Для моделювання випадкової величини Х з геометричним розподілом необхідно задати таблицю її значень та їх ймовірність
Прикладом випадкової величини з таким розподілом може бути загальна кількість випробувань, які потрібно провести до першого успішного випробування, наприклад, кількість пострілів, які потрібно виконати до першого попадання в ціль.

Моделювання неперервних випадкових величин.
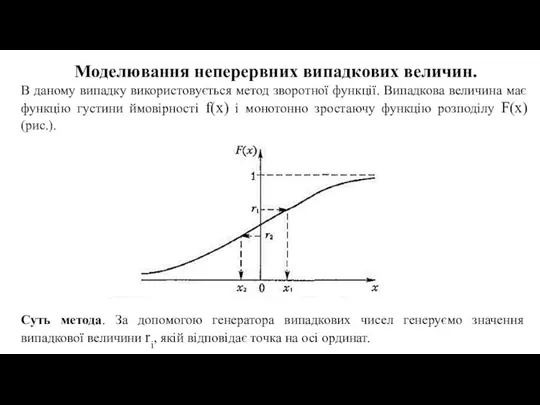
В даному випадку використовується метод зворотної функції. Випадкова величина має функцію густини ймовірності f(x) і монотонно зростаючу функцію розподілу F(x) (рис.).
Суть метода. За допомогою генератора випадкових чисел генеруємо значення випадкової величини ri, якій відповідає точка на осі ординат.

0, x < a
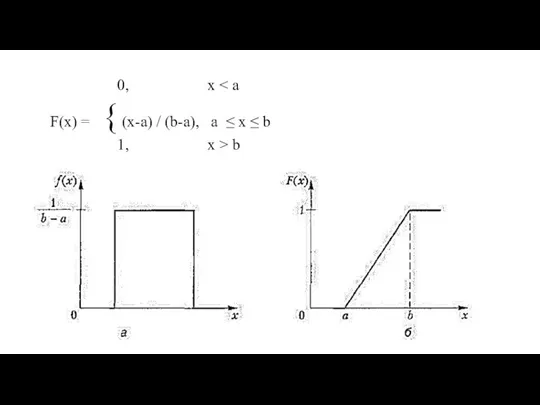
F(x) = { (x-a) / (b-a), a ≤ x ≤ b
1, x > b
Графики функций плотности f(x) и вероятности F(x) изображены на рис.

У мові GPSS такий розподіл часто використовується в блоках Advance для моделювання затримки проходження інформації або під час генерування потоків транзактов в блоках GENERATE.
Наприклад, щоб згенерувати потік транзактов, які надходять в модель кожні 5 ± 2 хвилини, використовують блок GENERATE 5.2.
Приклади реальних задач, в яких виникає необхідність моделювання рівномірно розподілених випадкових величин, - аналіз помилок округлення під час проведення числових розрахунків (точність задається числом десяткових знаків), час переміщення головок в магнітних накопичувачах (мінімальне і максимальне час), відхилення від графіка руху транспортних засобів (наприклад, метро).

Пуассонівський потік.
Розглянемо моделювання пуассонівского потоку з інтенсивністю λ, основна властивість якого полягає в тому, що ймовірність надходження k вимог протягом інтервалу тривалістю t становить:

Для пуассонівского потоку інтервали часу між надходженнями двох сусідніх вимог мають експонентний закон розподілу.
Тому для його моделювання досить отримати ряд чисел з таким розподілом.
Це можна реалізувати за допомогою методу зворотного функції, якщо ряд випадкових чисел ri рівномірно розподілених в інтервалі [0,1] перетворити відповідно до функції, зворотної експоненційної функції розподілу

де tj – j-й проміжок часу між надходженнями двох сусідніх вимог, - середнє значення проміжку часу між надходженнями двох сусідніх вимог, rj – j – число в послідовності випадкових чисел з рівномірним розподілом в інтервалі [0,1].
В мові GPSS для моделювання пуассонівського потоку вимог з = = 2 години використовується блок GENERATE 120 (одиниця часу в моделі 1 хвилина).

Нормальний розподіл.
Випадкова величина Х має нормальний розподіл (розподіл Гауса), якщо її густина розподілу ймовірностей описується законом:
де m – математичне сподівання, σ – середньоквадратичне відхилення.
Функція розподілу нормально розподіленої величини Х має вигляд:

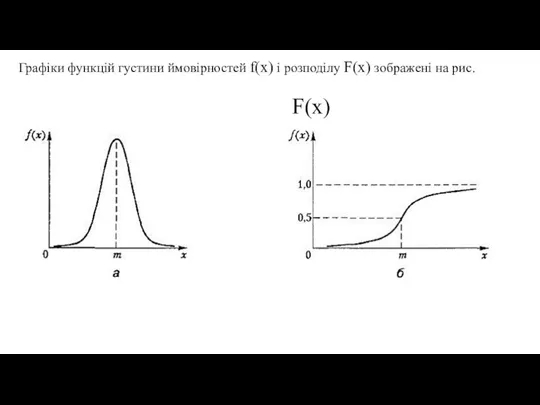
Графіки функцій густини ймовірностей f(x) і розподілу F(x) зображені на рис.
F(x)

Збір статистичних даних для отримання оцінок характеристик випадкових величин.
Основними елементами, з сукупності яких складається імовірнісна модель методу статистичних випробувань, є випадкові реалізації.
Очевидно, що при вирішенні деякої задачі визначення характеристик або параметрів вихідного випадкового процесу повинен бути визначений цей випадковий процес.
Шуканими величинами при використанні методу статистичних випробувань є оцінки:

- ймовірності настання деякої події;
- математичного очікування випадкової величини;
- дисперсії випадкової величини;
- коефіцієнтів коваріації або кореляції випадкової величини.
Для оцінки ймовірності р настання деякої події А використовується частота настання цієї події:
де m – частота настания події, а N – число дослідів.

Для оцінки математичного очікування випадкової величини використовується середнє значення
де хi – i-а реалізація випадкової величини.
Для оцінки дисперсії випадкової величини ξ використовують фор­мулу
де S2 – оцінка дисперсії випадкової величини ξ.

Безпосередньо використовувати ці формули для обчислення дисперсії складно, оскільки середнє значення змінюється в міру накопичення хi, тобто потрібно запам'ятовувати всі N значень хi.
Тому для обчислення використовують формулу:
В цьому випадку достатньо накопичити дві суми значень – хi и хi2.

Для випадкових величин ξ та η з можливими значеннями хk, yk оцінка корреляційного момента визначається так:
або в зручній для обчислень формі:

Визначення кількості реалізацій
Точність оцінювання параметрів системи, які отримують під час обробки результатів моделювання, залежить від кількості випробувань N.
Обсяг вибірки N завжди обмежений, тому раніше розглянуті оцінки матимуть різні похибки і дисперсії.
Якщо потрібно оцінити значення деякого параметра а за результатами моделювання xi, то в якості його оцінки потрібно брати величину , яка є функцією всіх значень xi.

Статистична оцінка також є випадковою величиной, тому вона буде відрізнятися від а, тобто
|a - | < ε, ε – точність або помилка оцінки.
Ймовірність того, що ця нерівність виконується, позначимо α:
P(| a - || < ε) ≥ α (1), де
ε – довірчий інтервал для α, довжина якого дорівнює 2ε, а α - довірчий рівень або надійність оцінки.
Вираз (1) використовують для визначення точності результатів статистичних випробувань.

Оцінка ймовірності.
Припустимо, що метою моделювання є оцінка ймовірності настання деякої події А, яка визначає стан системи.
У кожній з N реалізацій процесу настання події А є випадковою величиною ξ, яка приймає значення x1 = 1 з ймовірністю p і x2 = 0 з ймовірністю 1 - p.
Тоді можна визначити математичне очікування і дисперсію відповідно до формулами:
Як оцінку p використовують частоту настання події А.
За умови, що N задано, для отримання цієї оцінки досить накопичувати m:

Xi – настання події А в реалізації i.
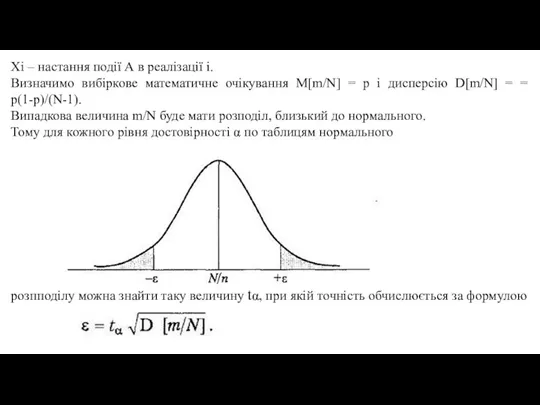
Визначимо вибіркове математичне очікування M[m/N] = p і дисперсію D[m/N] = = p(1-p)/(N-1).
Випадкова величина m/N буде мати розподіл, близький до нормального.
Тому для кожного рівня достовірності α по таблицям нормального
розпподілу можна знайти таку величину tα, при якій точність обчислюється за формулою

Якщо α = 0.95, то tα = 1.96, а якщо α = 0.003, то tα = 3.
Підставимо в останню формулу вираз дисперсії:
звідки

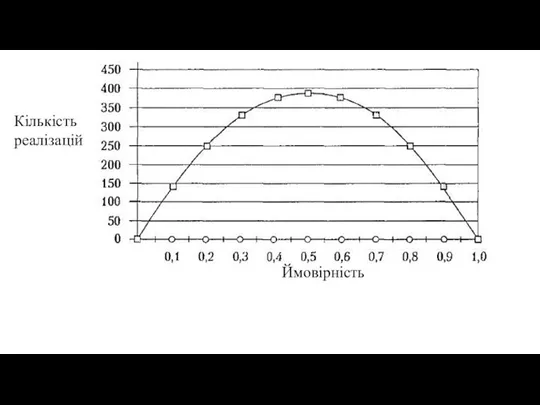
З останньої формули видно, що при p = 1 або p = 0, кількість реалізацій, які необхідно зробити для підтвердження того, що подія А настає (чи ні), дорівнює 1.
Але оскільки ймовірність p заздалегідь невідома, проводять випробування (N = 50 ... 100), оцінюють частоту m / N і підставляють її значення в останній вираз замість p, після чого визначають остаточну кількість реалізацій.
Графік числа реалізацій для α = 0.05 та різних значень p, якщо ε = 0.05, наведено на рис.

Кількість
реалізацій
Ймовірність