Задачи на вычисление углов в ЕГЭ

*
I. Задачи на нахождение углов между прямыми.
Какие типы задач предлагаются на ЕГЭ
III. Задачи на нахождение углов, образованных двумя плоскостями или полуплоскостями, двугранных углов.
II. Задачи на нахождение углов между прямой и плоскостью.

*
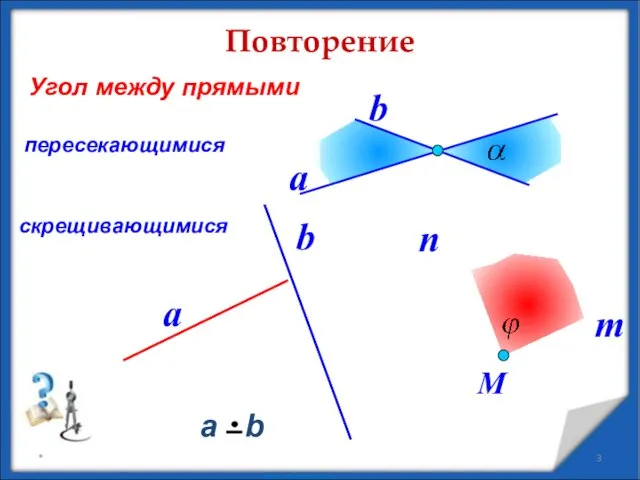
Повторение
Угол между прямыми
a
b
пересекающимися
скрещивающимися
a
b
М

*
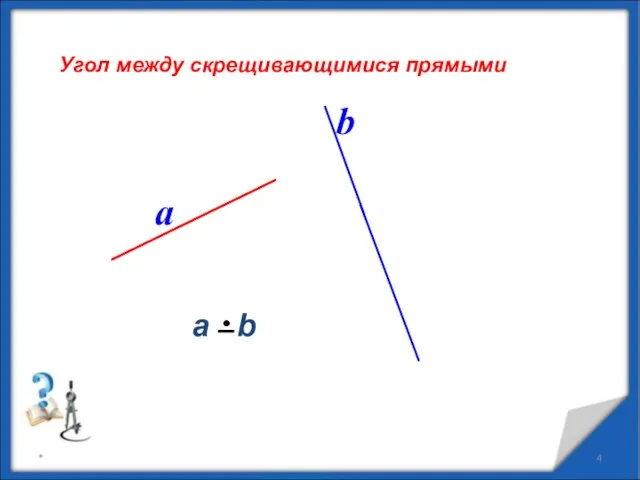
Угол между скрещивающимися прямыми
a
b

*
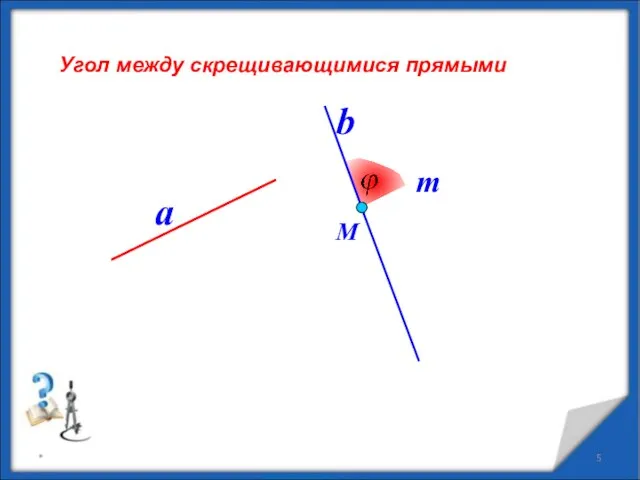
Угол между скрещивающимися прямыми
a
b
М
m

*
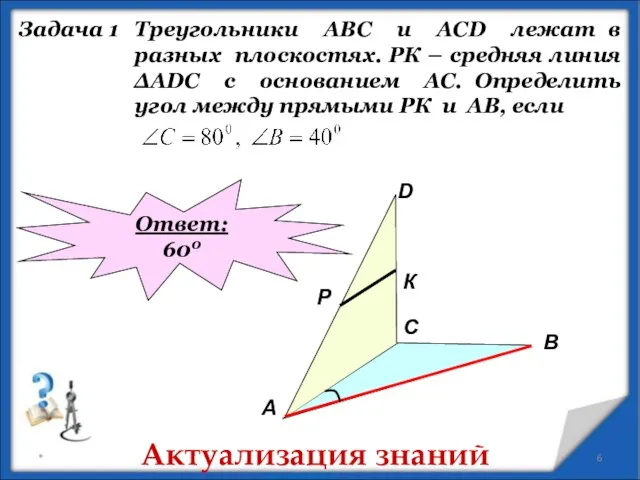
Треугольники АВС и АСD лежат в разных плоскостях. РК – средняя линия ∆АDC с основанием АС. Определить угол между прямыми РК и АВ, если
А
В
С
D
P
К
Ответ:
600
Задача 1
Актуализация знаний

*
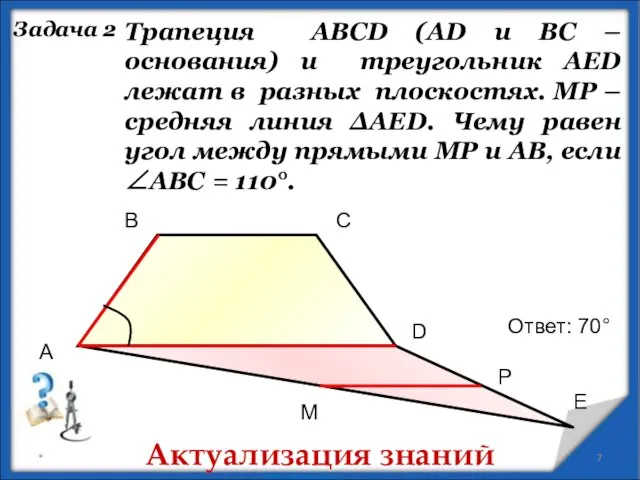
Задача 2
Трапеция АВСD (AD и ВС – основания) и треугольник АЕD лежат в разных плоскостях. МР – средняя линия ∆АЕD. Чему равен угол между прямыми МР и АВ, если ∠АВС = 110°.
А
С
В
D
E
M
P
Ответ: 70°
Актуализация знаний

*
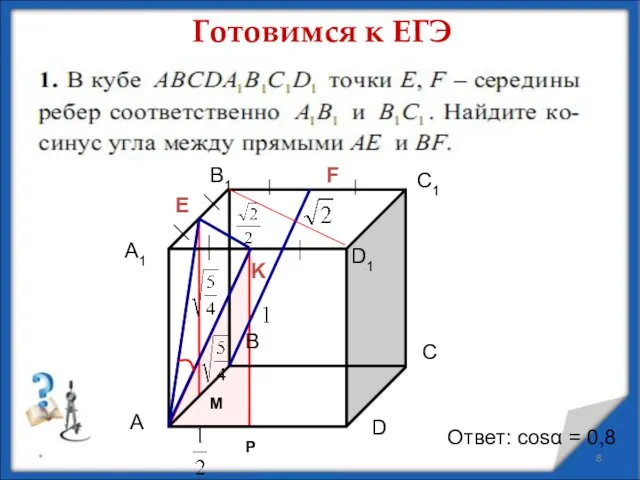
Готовимся к ЕГЭ
Е
F
K
Ответ: cosα = 0,8
Р
М

*
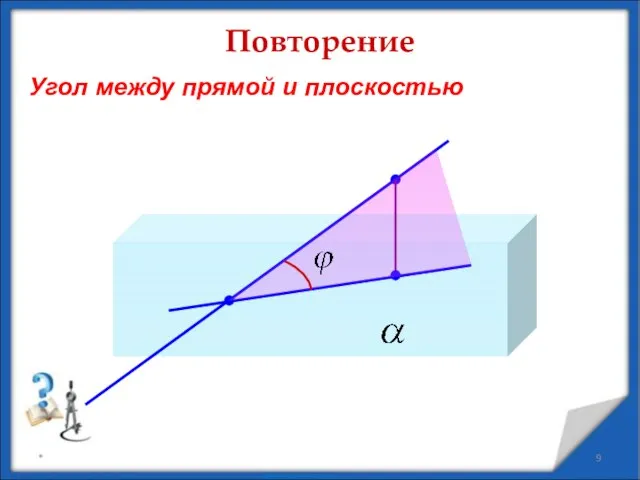
Повторение
Угол между прямой и плоскостью

*
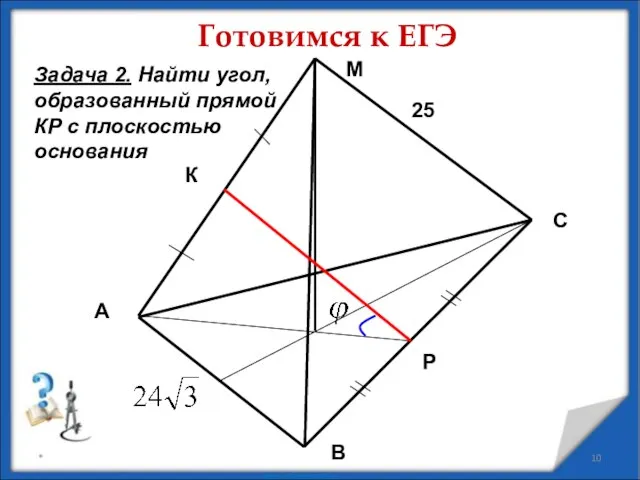
Готовимся к ЕГЭ
Задача 2. Найти угол, образованный прямой КР с плоскостью основания
А
В
С
М
К
Р
25

*
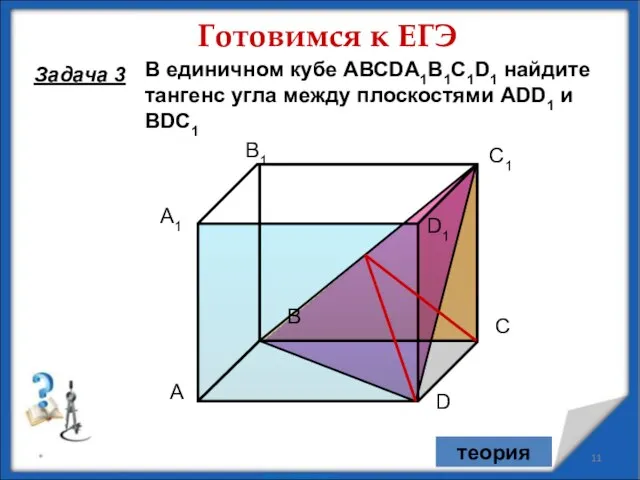
А
С
В
D
А1
С1
В1
D1
В единичном кубе АВСDA1B1C1D1 найдите тангенс угла между плоскостями ADD1 и BDC1
Готовимся к ЕГЭ
Задача 3
теория

*
Домашнее задание
1. Решить три задачи на все рассмотренные на занятии типы.
2. Повторить к следующему занятию понятия расстояний от точки до прямой, от прямой до параллельной ей плоскости, между параллельными плоскостями.

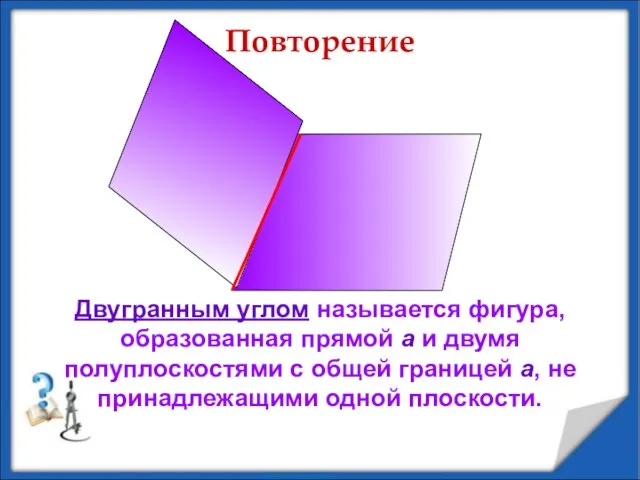
Двугранным углом называется фигура, образованная прямой а и двумя полуплоскостями с общей границей а, не принадлежащими одной плоскости.
Повторение

*
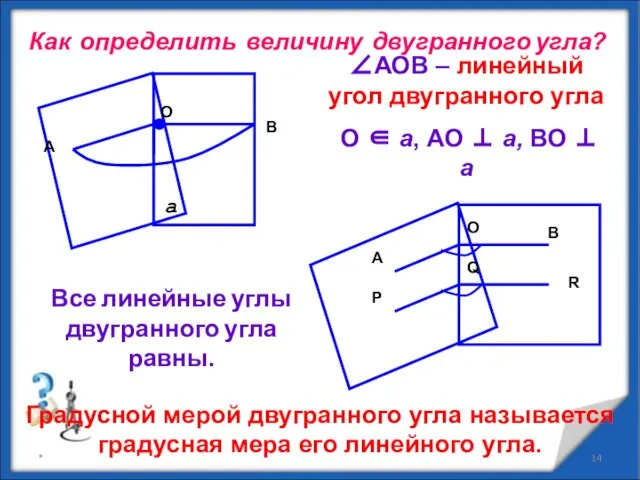
Как определить величину двугранного угла?
B
A
O
∠АОВ – линейный угол двугранного угла
О ∈ а, АО ⊥ а, ВО ⊥ а
а
B
A
O
R
P
Q
Все линейные углы двугранного угла равны.
Градусной мерой двугранного угла называется градусная мера его линейного угла.

*
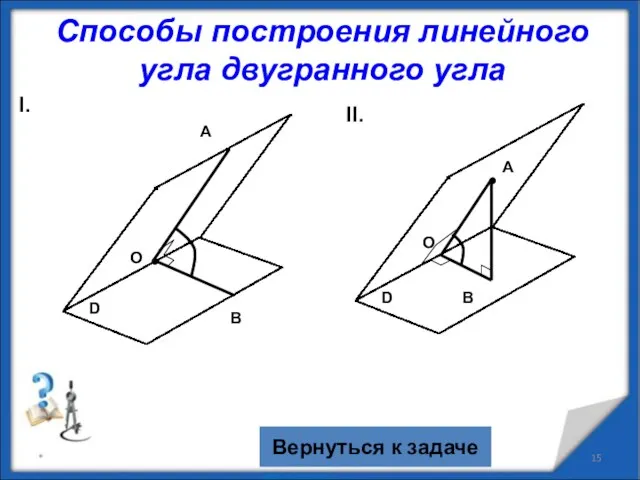
Способы построения линейного угла двугранного угла
I.
O
A
B
II.
A
O
B
D
D
Вернуться к задаче