Содержание
- 5. Рис. 26.1.
- 6. Выясним физический смысл χ и β Обозначим через τ -время, в течение которого амплитуда А уменьшается
- 8. Где ψ = arctg(β/ω). График этой функции изображен на рис. 26.2. Рис. 26.2.
- 10. перестает быть периодическим. При β > ω0 корни характеристичес- кого уравнения становятся вещественными и решение дифферен-
- 11. Это условие будет выполнено в том случае, если выведенной из положения равновесия системе сообщить достаточно сильный
- 14. Рис. 26.27.
- 17. Скачать презентацию
Слайд 5Рис. 26.1.
Рис. 26.1.

Слайд 6Выясним физический смысл χ и β
Обозначим через τ -время, в течение которого
Выясним физический смысл χ и β
Обозначим через τ -время, в течение которого

амплитуда А
уменьшается в e раз.
A0 /AΊ = eβτ = e1, откуда βτ = 1, β = 1/τ
Следовательно, коэффициент затухания β - есть физическая
величина, обратная времени, в течении которого амплитуда
уменьшается в е раз. τ - время релаксации.
Пусть Nе число колебаний, после которых амплитуда
уменьшается в e раз, τ - время этих колебаний,
тогда τ = ΝΤ, Τ= τ /Ν и χ = βΤ = τ / τ N = 1/N, χ = 1/N
Следовательно, логарифмический декремент затухания χ есть
физическая величина, обратная числу колебаний, по истечению
которых амплитуда А уменьшается в e раз. Если χ = 0,01,
то N = 100.
уменьшается в e раз.
A0 /AΊ = eβτ = e1, откуда βτ = 1, β = 1/τ
Следовательно, коэффициент затухания β - есть физическая
величина, обратная времени, в течении которого амплитуда
уменьшается в е раз. τ - время релаксации.
Пусть Nе число колебаний, после которых амплитуда
уменьшается в e раз, τ - время этих колебаний,
тогда τ = ΝΤ, Τ= τ /Ν и χ = βΤ = τ / τ N = 1/N, χ = 1/N
Следовательно, логарифмический декремент затухания χ есть
физическая величина, обратная числу колебаний, по истечению
которых амплитуда А уменьшается в e раз. Если χ = 0,01,
то N = 100.
Слайд 8Где ψ = arctg(β/ω). График этой функции изображен на рис. 26.2.
Рис. 26.2.
Где ψ = arctg(β/ω). График этой функции изображен на рис. 26.2.
Рис. 26.2.

Слайд 10перестает быть периодическим. При β > ω0 корни характеристичес-
кого уравнения становятся вещественными
перестает быть периодическим. При β > ω0 корни характеристичес-
кого уравнения становятся вещественными

и решение дифферен-
циального уравнения (26.1) оказывается равным сумме двух
экспонент: х = С1е-λ1t + С2е-λ2t , где λ1= - β +iω, а λ2= - β - iω, а С1 и
С2 - вещественные константы, значения которых зависят от нача-
льных условий (от х0 и υ0). Следовательно движение носит
апериодический (непериодический) характер – выведенная из поло-
жения равновесия система возвращается в положение равновесия,
не совершая колебаний. На рис. 26.26 показано три возможных
способа возвращения системы к положению равновесия при
апериодическом движении. Каким из этих способов приходит
циального уравнения (26.1) оказывается равным сумме двух
экспонент: х = С1е-λ1t + С2е-λ2t , где λ1= - β +iω, а λ2= - β - iω, а С1 и
С2 - вещественные константы, значения которых зависят от нача-
льных условий (от х0 и υ0). Следовательно движение носит
апериодический (непериодический) характер – выведенная из поло-
жения равновесия система возвращается в положение равновесия,
не совершая колебаний. На рис. 26.26 показано три возможных
способа возвращения системы к положению равновесия при
апериодическом движении. Каким из этих способов приходит
Рис. 26.26.
Слайд 11Это условие будет выполнено в том случае, если выведенной из
положения равновесия системе
Это условие будет выполнено в том случае, если выведенной из
положения равновесия системе

сообщить достаточно сильный
толчок к положению равновесия. Если, отведя систему из
положения равновесия, отпустить ее без толчка (т.е. с υ0 = 0) или
сообщить ей толчок недостаточной силы (такой, что υ0 окажется
меньше определяемой условием (26.6)), движение будет
Происходить в соответствии с кривой А на рис. 26.26.
толчок к положению равновесия. Если, отведя систему из
положения равновесия, отпустить ее без толчка (т.е. с υ0 = 0) или
сообщить ей толчок недостаточной силы (такой, что υ0 окажется
меньше определяемой условием (26.6)), движение будет
Происходить в соответствии с кривой А на рис. 26.26.
Слайд 14Рис. 26.27.
Рис. 26.27.

- Предыдущая
Криволинейное движениеСледующая -
Расчет сопротивления проводников







 Проведение проверки по факту пожара, произошедшего на теплоходе Саманта Смит
Проведение проверки по факту пожара, произошедшего на теплоходе Саманта Смит Культура и мораль
Культура и мораль Элементы БД
Элементы БД Кинематика. Относительность движения
Кинематика. Относительность движения Презентация на тему Питерский район
Презентация на тему Питерский район  И за день, и за ночь (Спасибо, Господи)
И за день, и за ночь (Спасибо, Господи) Серебряный век русской культуры
Серебряный век русской культуры Мировая художественная культура «Зарождение искусства»
Мировая художественная культура «Зарождение искусства» 2011 год объявлен в России Годом космонавтики 50-летие полёта в космос Ю.А.Гагарина.
2011 год объявлен в России Годом космонавтики 50-летие полёта в космос Ю.А.Гагарина. Публичный доклад
Публичный доклад Паспортизация туристских маршрутов, сертификация туристских услуг и услуг средств размещения
Паспортизация туристских маршрутов, сертификация туристских услуг и услуг средств размещения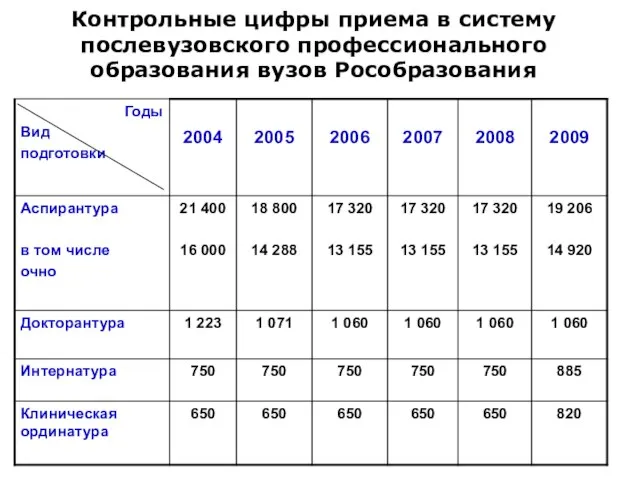 Контрольные цифры приема в систему послевузовского профессионального образования вузов Рособразования
Контрольные цифры приема в систему послевузовского профессионального образования вузов Рособразования А.С. Пушкин глазами художников
А.С. Пушкин глазами художников Изменения в политической системе
Изменения в политической системе Предложение Монблан
Предложение Монблан Автострахование в России: проблемы и перспективы
Автострахование в России: проблемы и перспективы Чытачам Брылеўскай бібліятэкі 10.04.2019 г
Чытачам Брылеўскай бібліятэкі 10.04.2019 г Эрмитаж
Эрмитаж Пропедевтика изучения частей речи
Пропедевтика изучения частей речи Интернет вещи
Интернет вещи Графический интерфейс LINUX
Графический интерфейс LINUX Права животных в Великобритании
Права животных в Великобритании КЛАССИФИКАЦИЯ РАСТЕНИЙ. СЕМЕЙСТВО РОЗОЦВЕТНЫХ
КЛАССИФИКАЦИЯ РАСТЕНИЙ. СЕМЕЙСТВО РОЗОЦВЕТНЫХ Анализ половозрастной структуры населения
Анализ половозрастной структуры населения Национальный татарский костюм
Национальный татарский костюм Появление товарного производства. Складывание торговых путей. Установление торговых связей Руси с другими гос-ами и народами (9-14 в
Появление товарного производства. Складывание торговых путей. Установление торговых связей Руси с другими гос-ами и народами (9-14 в Под Покровом Божией Матери
Под Покровом Божией Матери manikyur (1)
manikyur (1)