Слайд 2Содержание
Общие данные
Схематическое изображение золотого сечения
Схематическое изображение золотого сечения
Ряд Фибоначчи
Изображение Фибоначчи
История золотого

сечения
Изображение Пифагора
История золотого сечения
Примеры золотого сечения в природе
Слайд 3Общие данные
Золотое сечение — деление непрерывной величины на части в таком отношении,

при котором меньшая часть так относится к большей, как большая ко всей величине.
Численно равно 1.618
Другие названия: золотая пропорция, деление в крайнем и среднем отношении, гармоническое деление
Слайд 4Схематическое изображение золотого сечения
a : b = b : c или с
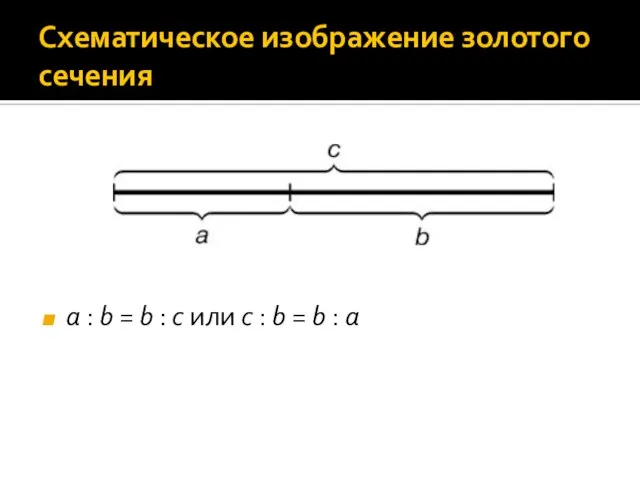
: b = b : а
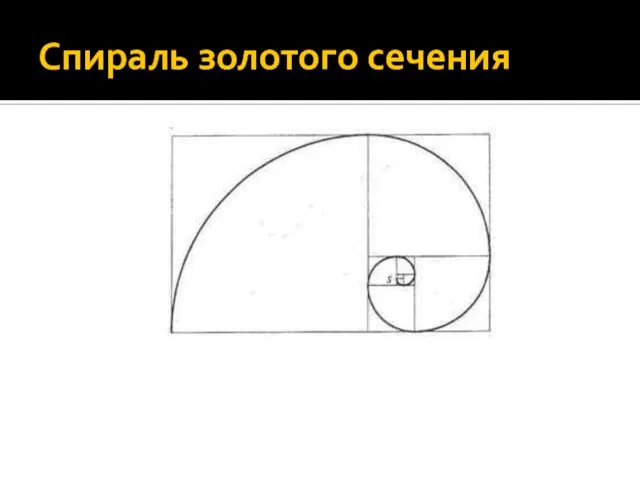
Слайд 5Ряд Фибоначчи
Особенность последовательности чисел состоит в том, что каждый ее член,

начиная с третьего, равен сумме двух предыдущих 2 + 3 = 5; 3 + 5 = 8; 5 + 8 = 13, 8 + 13 = 21; 13 + 21 = 34 и т.д., а отношение смежных чисел ряда приближается к отношению золотого деления.
Все исследователи золотого деления в растительном и в животном мире, не говоря уже об искусстве, неизменно приходили к этому ряду как арифметическому выражению закона золотого деления.
Слайд 7История золотого сечения
Принято считать, что понятие о золотом делении ввел в

научный обиход Пифагор.
Есть предположение, что Пифагор (570—490 гг. до н. э.) свое знание золотого деления позаимствовал у египтян и вавилонян.
Платон (428 или 427 до н. э. — 348 или 347 до н. э.) также знал о золотом делении. Его диалог «Тимей» посвящен математическим и эстетическим воззрениям школы Пифагора и, в частности, вопросам золотого деления.
Слайд 9История золотого сечения
В эпоху Возрождения усиливается интерес к золотому делению среди ученых

и художников в связи с его применением как в геометрии, так и в искусстве, особенно в архитектуре.
Великий астроном XVI в. Иоганн Кеплер (27.12.1571 – 15.11.1630) назвал золотое сечение одним из сокровищ геометрии. Он первый обращает внимание на значение золотой пропорции для ботаники.
Слайд 10Принципы формообразования в природе
Рост вверх или расстилание по поверхности земли.
Винтообразное и

спиралевидное расположение листьев на ветках деревьев подметили давно.
Спираль увидели в расположении семян подсолнечника, в шишках сосны, ананасах, кактусах и т.д.
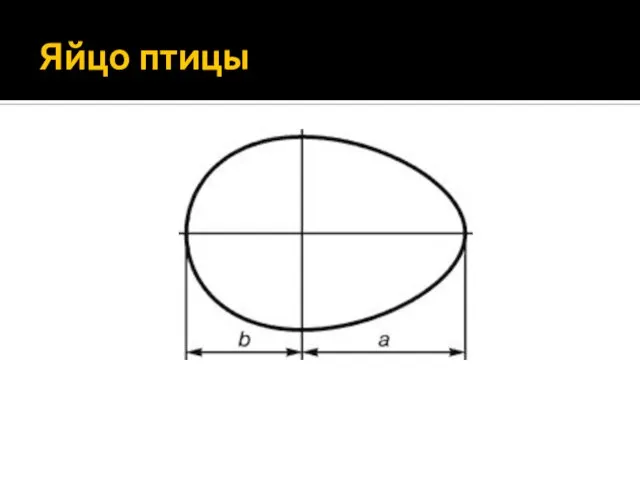
Слайд 11Примеры золотого сечения в природе
В расположении листьев на ветке, семян подсолнечника, шишек

сосны проявляет себя ряд Фибоначчи, а стало быть, проявляет себя закон золотого сечения.
Паук плетет паутину спиралеобразно.
Спиралью закручивается ураган.
Испуганное стадо северных оленей разбегается по спирали. Молекула ДНК закручена двойной спиралью.
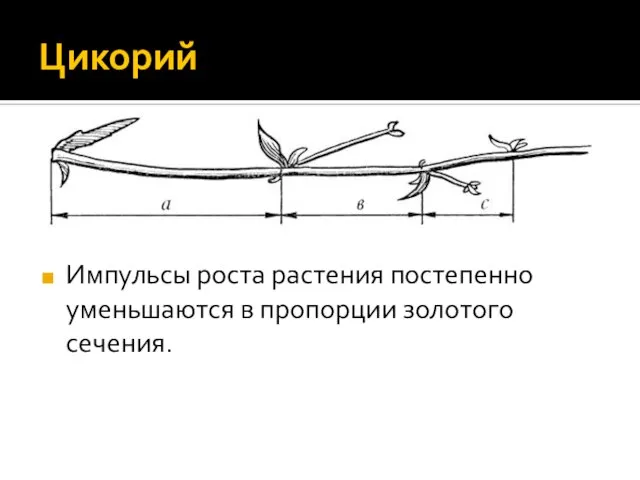
Слайд 12Цикорий
Импульсы роста растения постепенно уменьшаются в пропорции золотого сечения.
Слайд 13Ящерица живородящая
Длина хвоста так относится к длине остального тела, как 62
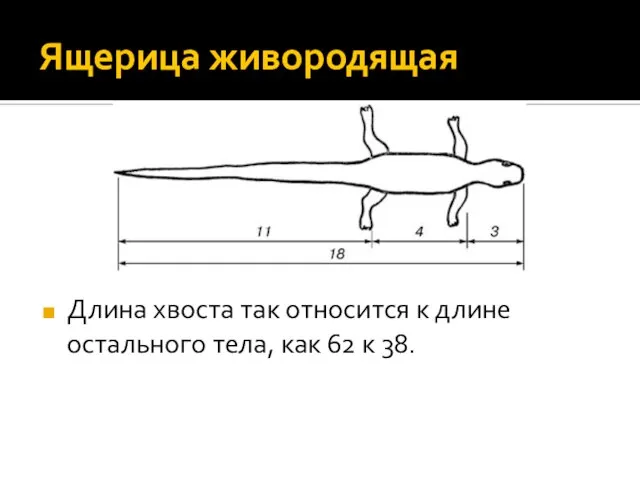
к 38.
Слайд 14Еще примеры
Закономерности «золотой» симметрии проявляются в энергетических переходах элементарных частиц, в строении

некоторых химических соединений, в планетарных и космических системах, в генных структурах живых организмов.
Эти закономерности, как указано выше, есть в строении отдельных органов человека и тела в целом, а также проявляются в биоритмах и функционировании головного мозга и зрительного восприятия.
Слайд 16Золотые пропорции в частях тела человека
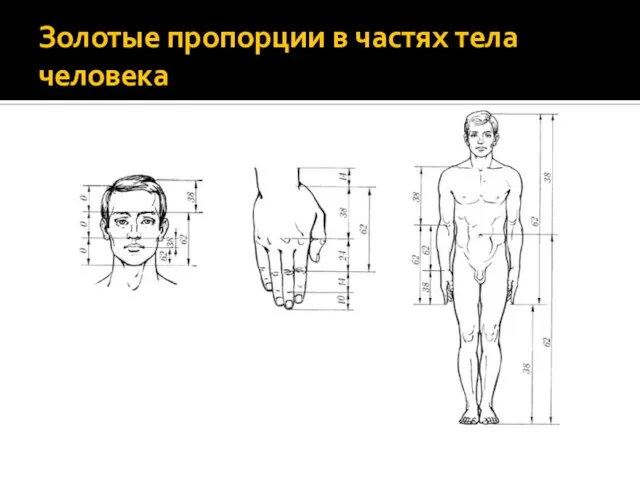
Слайд 17Золотые пропорции в литературе
Стихотворения подобны музыкальным произведениям; в них также существуют кульминационные

пункты, которые делят стихотворение в пропорции золотого сечения.
Роман "Евгений Онегин" состоит из 8 глав, в каждой из них в среднем около 50 стихов. Наиболее совершенной, наиболее отточенной и эмоционально насыщенной является восьмая глава. В ней 51 стих. Вместе с письмом Евгения к Татьяне (60 строк) это точно соответствует числу Фибоначчи 55!
Слайд 18«Рукою стиснув пистолет,
глядит на Ленского Евгений…»

Слайд 19Золотое сечение в архитектуре
Парфенон

Слайд 20Золотое сечение и пирамиды
Пропорции пирамиды Хеопса, храмов, барельефов, предметов быта и украшений

из гробницы Тутанхамона свидетельствуют, что египетские мастера пользовались соотношениями золотого деления при их создании.
Не только египетские пиpамиды постpоены в соответствии с совеpшенными пpопоpциями золотого сечения; то же самое явление обнаpужено и у мексиканских пиpамид. Hа попеpечном сечении пиpамиды видна фоpма, подобная лестнице.В пеpвом яpусе 16 ступеней, во втоpом 42 ступени и в тpетьем - 68 ступеней.
Слайд 21Собор Василия Блаженного
На этом плане хорошо видно, что части здания соотносятся в

пропорции золотого сечения
Слайд 22Аполлон Бельведерский
Знаменитая статуя Аполлона Бельведерского также состоит из частей, делящихся по золотым

отношениям.
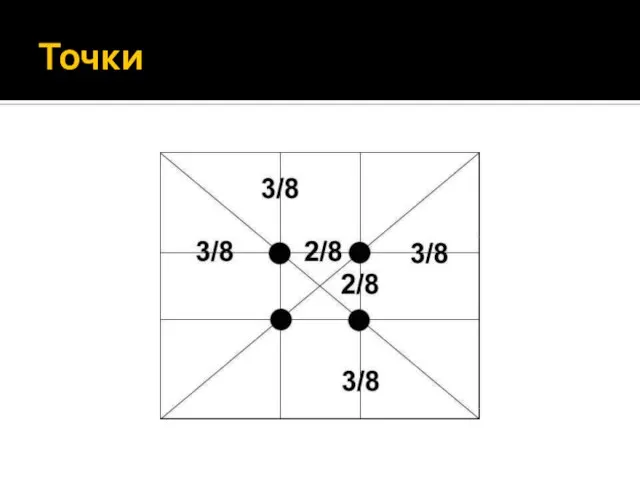
Слайд 23Золотое сечение и живопись
Еще в эпоху Возрождения художники открыли, что любая картина

имеет определенные точки, невольно приковывающие наше внимание, так называемые зрительные центры.
При этом абсолютно неважно, какой формат имеет картина - горизонтальный или вертикальный. Таких точек всего четыре, они делят величину изображения по горизонтали и вертикали в золотом сечении.
Слайд 27Спираль золотого сечения на гравюре Рафаэля

Слайд 28"Всеобщий закон пропорциональности" Цейзинга
В подтверждение этого закона он приводит данные об

отношениях взаимных расстояний между собой небесных светил, отвечающих золотому сечению, устанавливает такие же отношения в строении человеческой фигуры, в конфигурации минералов, растений, в звуковых аккордах музыки в архитектурных произведениях.
Слайд 29Вывод
Он напрашивается сам собой – все во вселенной подчинено общим законам, которые

нужно учитывать для общечеловеческого развития.
Самая большая загадка заключается в том, почему наша общая система – золотое сечение.
Этот вопрос пронизывает абсолютно все науки, хотя и имеет математические корни.
Лично я была глубоко поражена подобной взаимосвязью во вселенной и лишний раз убедилась в том, как тесно связано все в мире.

























 Архітектура України ХІХ ст
Архітектура України ХІХ ст Обучение правилам чтения
Обучение правилам чтения Презентация на тему Названия месяцев и дней недели
Презентация на тему Названия месяцев и дней недели  Нижний Новгород, 2020
Нижний Новгород, 2020 Weddings in different countries
Weddings in different countries Лев Николаевич Толстой
Лев Николаевич Толстой Название бизнес-плана
Название бизнес-плана 90 лет на планете Земля
90 лет на планете Земля Gli ospiti di Jerry. Chi è?
Gli ospiti di Jerry. Chi è? Первый день творения (земля, вода, небо)
Первый день творения (земля, вода, небо) Электроснабжение объектов
Электроснабжение объектов Генерация вероятностных автоматов методами Reinforcement Learning
Генерация вероятностных автоматов методами Reinforcement Learning Взаимодействие токов. Магнитное поле
Взаимодействие токов. Магнитное поле Летние Олимпийские игры 2012 в Лондоне
Летние Олимпийские игры 2012 в Лондоне Финансовый калькулятор
Финансовый калькулятор Абсцесс и гангрена легких
Абсцесс и гангрена легких Marshrutnaya set s perechnem ostanovochnyh punktov
Marshrutnaya set s perechnem ostanovochnyh punktov Nikolay Mikhaylovich Przhevalsky and Russian geography and exploration.
Nikolay Mikhaylovich Przhevalsky and Russian geography and exploration. Дисграфия как одна из причин школьной неуспешности по русскому языку
Дисграфия как одна из причин школьной неуспешности по русскому языку Отчет по производственной практике
Отчет по производственной практике Публичный отчет директора МВ(с)ОУ О(с)ОШ №1
Публичный отчет директора МВ(с)ОУ О(с)ОШ №1 СПБ 2018-2019. Наше маленькое путешествие
СПБ 2018-2019. Наше маленькое путешествие Иван Грозный
Иван Грозный Артериальная гипертония.Антигипертензивные препараты.
Артериальная гипертония.Антигипертензивные препараты. Буквы потерялись
Буквы потерялись МЕТОДЫ ДИАГНОСТИКИ ИНФЕКЦИОННЫХ ЗАБОЛЕВАНИЙ
МЕТОДЫ ДИАГНОСТИКИ ИНФЕКЦИОННЫХ ЗАБОЛЕВАНИЙ Дом и вещи
Дом и вещи Презентация на тему Великая отечественная война на Кубани
Презентация на тему Великая отечественная война на Кубани