Функциональные зависимости. Нормализация отношений

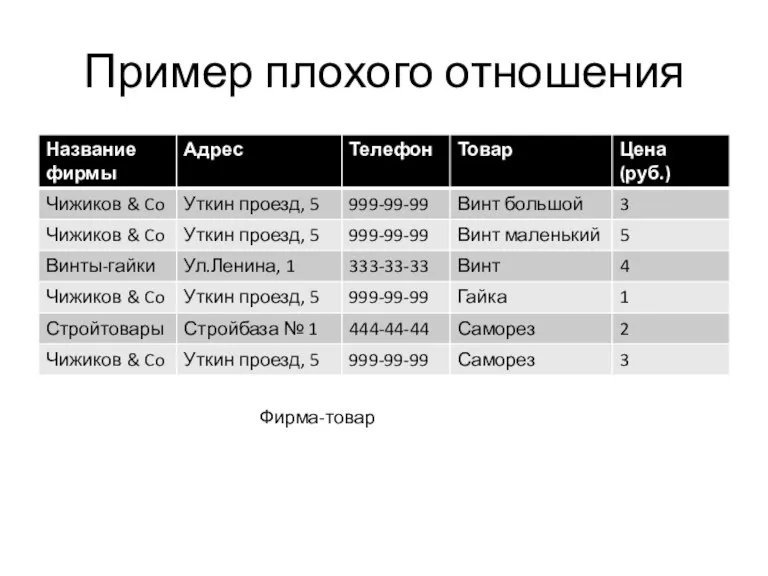
Пример плохого отношения
Фирма-товар

Недостатки
Избыточность
Аномалии изменения
Аномалии удаления
Аномалии добавления

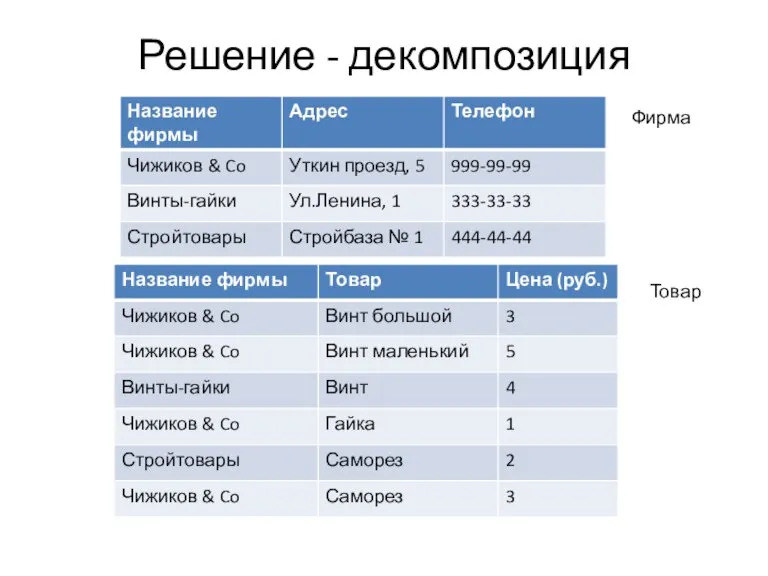
Решение - декомпозиция
Фирма
Товар

Декомпозиция
R {A1, A2, … An}
S {B1, B2, … Bm} T {C1, C2, … Ck}
1) {A1, A2, … An}= {B1, B2, … Bm}∪ {C1, C2, … Ck}
2) S=π B1, B2, … Bm (R)
3) T=π C1, C2, … Ck (R)

Ограничения на значения:
семантические, т.е. корректность отдельных значений (год рождения больше нуля);
ограничения на значения, которые зависят только от равенства или неравенства значений (совпадают ли компоненты двух кортежей); наиболее важные ограничения называются функциональной зависимостью.

Функциональные зависимости
R {A1, A2, … An}
X, Y ⊂ {A1, A2, … An}
X → Y если любому значению X соответствует в точности одно значение Y
X → Y ⇔ |πY(σX=x(R))|≤1
Название фирмы → Адрес, телефон.
Название фирмы, товар → Цена

A1, A2, … An → B1, B2, … Bm
ФЗ бывают:
Тривиальные
{B1, B2, … Bm } ⊂ {A1, A2, … An }
Нетривиальные
{B1, B2, … Bm } ⊄ {A1, A2, … An }
{A1, A2, … An } ∩ {B1, B2, … Bm } ≠∅
Полностью нетривиальные
{A1, A2, … An } ∩ {B1, B2, … Bm } =∅

Ключ
Ключ – набор атрибутов, который функционально определяет все остальные
F – множество функциональных зависимостей, заданных на отношении R
A→C называется транзитивной, если существует такой атрибут B, что имеются функциональные зависимости A→B и B→C и отсутствует функциональная зависимость C→A

Замыкание множества атрибутов
R {A1, A2, … An}
{B1, B2, … Bm } ⊂ {A1, A2, … An }
F – мн-во ФЗ
Z={B1, B2, … Bm }+
Z0 := {B1, B2, … Bm }
BiBj → C
Z1:=Z0∪C
{B1, B2, … Bm } += {A1, A2, … An } ⇒
{B1, B2, … Bm } - ключ

Пример
R {A, B, C, D, E, F}
S = {A→D, AB→E, BF→E, CD→F, E→C}
{AE}+ ?

Пример
R {A, B, C, D, E, F}
S = {A→D, AB→E, BF→E, CD→F, E→C}
{AE}+ = ACDEF

Аксиомы Армстронга
если B⊂A, то A→B
рефлексивность;
если A→B, то AC→BC
пополнение;
если A→B и B→C, то A→C
транзитивность.

Правила вывода
(из аксиом Армстронга)
1. Объединение
Если X→Y и X→Z, то X→YZ.
X→Y + А2 = X→XY, X→Z + A2 = YX→YZ + A3 = X→YZ
2. Псевдотранзитивность
X→Y и WY→Z, то WX→Z.
X→Y +A2 = WX→WY. WY→Z + A3 = WX→Z.
3. Декомпозиция
Если X→Y и Z⊆Y, то X→Z.
А1 + А3.

Замыкание множества
функциональных зависимостей
F+ - множество всех зависимостей, которые можно вывести из F, называют замыканием множества ФЗ F
Любое множество функциональных зависимостей, из которого можно вывести все остальные ФЗ, называется базисом
Если ни одно из подмножеств базиса базисом не является, то такой базис минимален

Замыкание множества
функциональных зависимостей
R {A1, A2, … An}
F – мн-во ФЗ
B1, B2, … Bm → C
(B1, B2, … Bm → C) ∈F+ , if
C∈{B1, B2, … Bm }+

Пример:
R (A, B, C, D)
AB →C, C →D, D→A
Найти все нетривиальные ФЗ, которые следуют из заданных
Возможные ключи

Покрытие множества функциональных зависимостей
Множество ФЗ F2 называется покрытием множества ФЗ F1, если любая ФЗ, выводимая из F1, выводится также из F2.
F1+∈F2+
F1 и F2 называются эквивалентными, если F1+ = F2+.

Минимальное покрытие множества функциональных зависимостей
правая часть любой ФЗ из F является множеством из одного атрибута (простым атрибутом);
удаление любого атрибута из левой части любой ФЗ приводит к изменению замыкания F+;
удаление любой ФЗ из F приводит к изменению F+.

ДЕКОМПОЗИЦИЯ
Декомпозиция – это разбиение на множества, может быть пересекающиеся, такие, что их объединение – это исходное отношение.
Восстановить исходное отношение можно только естественным соединением.
Говорят, что декомпозиция обладает свойством соединения без потерь, если для любого отношения
r = πR1(r)▷◁ πR2(r) ▷◁ ... ▷◁ πRn(r).

А что происходит с зависимостями при декомпозиции?
Можно определить πZ(F): X→Y XY⊆Z
Декомпозиция сохраняет множество зависимостей, если из объединения всех проекций зависимостей логически следует F.

Проектирование
реляционных отношений
1 нормальная форма (НФ)– значения не являются множествами и кортежами.
Атрибут называется первичным, если входит в состав любого возможного ключа.
2 нормальная форма – 1 НФ + любой атрибут, не являющийся первичным, полностью зависит от любого его ключа, но не от подмножества ключа.
Фирма, Адрес, Телефон, Товар, Цена

3 НФ
Транзитивная зависимость: пусть A, B, C – атрибуты, A→B, B→C, A не зависит от B и B не зависит от C. Тогда говорят, что C транзитивно зависит от A.
3 нормальная форма – если отношение находится во 2 нормальной форме и любой атрибут, не являющийся первичным, нетранзитивно зависит от любого возможного ключа.

Примеры:
Универмаг, Товар, Номер отдела, Заведующий
Город, Индекс, Адрес

Примеры:
3 нормальная форма – (Город, Индекс, Адрес)
2 нормальная форма, но не 3 нормальная форма – (Универмаг, Товар, Номер отдела, Заведующий)
УТ→Н, УН→З, ключ – УТ.

НФ Бойса-Кодда
Нормальная форма Бойса–Кодда – если X→A, A∉X, то X⊇ключ R.
(Город, Индекс, Адрес) – 3 нормальная форма, но не форма Бойса–Кодда.
Если разобьем на две (Город, Индекс), (Индекс, Адрес), пропадает зависимость Город, Адрес→Индекс.

НФ Бойса-Кодда
(Город, Индекс, Адрес) – 3 нормальная форма, но не форма Бойса–Кодда. Если разобьем на две (Город, Индекс), (Индекс, Адрес), пропадает зависимость Город, Адрес→Индекс.

Вывод:
Каждая схема отношений может быть приведена к форме Бойса–Кодда, так что декомпозиция обладает свойством соединения без потерь.
Любая схема может быть приведена к 3 нормальной форме с соединением без потерь и с сохранением функциональной зависимости.
Но не всегда можно привести к форме Бойса–Кодда с сохранением функциональных зависимостей.

Шаги при декомпозиции
Находим минимальное покрытие множества функциональных зависимостей
Выделяем зависимость, нарушающую НФ
X → Y (и нет атрибутов, зависящих от Y).
Находим зависимости с такой же левой частью.
X → W, X → Z
Выделяем в отдельное отношение XYWZ
Из исходного отношения удаляем YWZ