Содержание
- 2. Постановка задачи распределения фондов минеральных удобрений сельскохозяйственной организации Задано сельскохозяйственная организация; план размещения культур по полям
- 3. Известно: относительно каждой элементарной культуры: сорт; система орошения; предшественник, его удобренность; физико-химические свойства почвы; рекомендуемые годовые
- 4. Требуется определить: какие дозы удобрений, в какие сроки и в каком ассортименте следует вносить под каждую
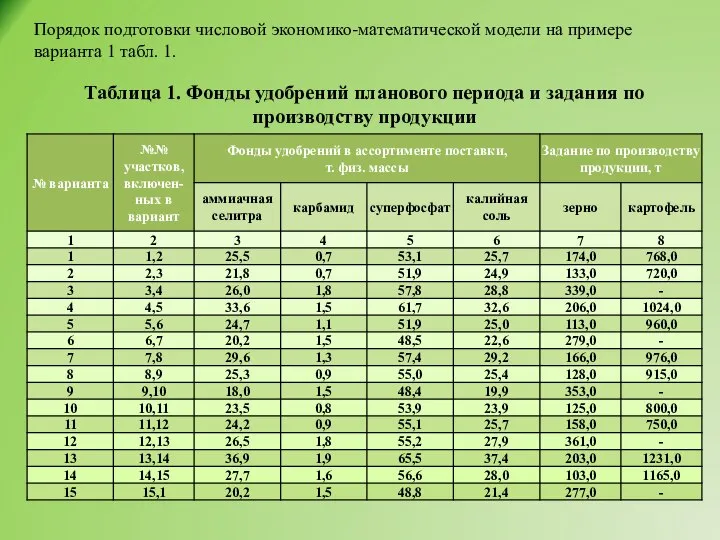
- 5. Порядок подготовки числовой экономико-математической модели на примере варианта 1 табл. 1. Таблица 1. Фонды удобрений планового
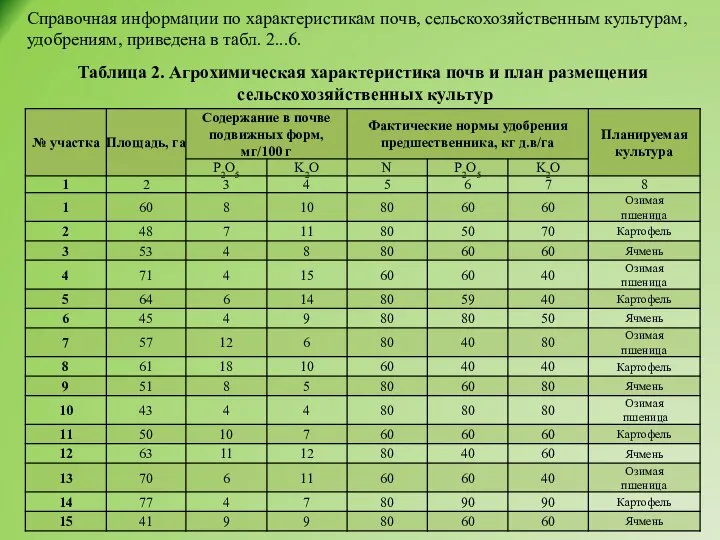
- 6. Справочная информации по характеристикам почв, сельскохозяйственным культурам, удобрениям, приведена в табл. 2...6. Таблица 2. Агрохимическая характеристика
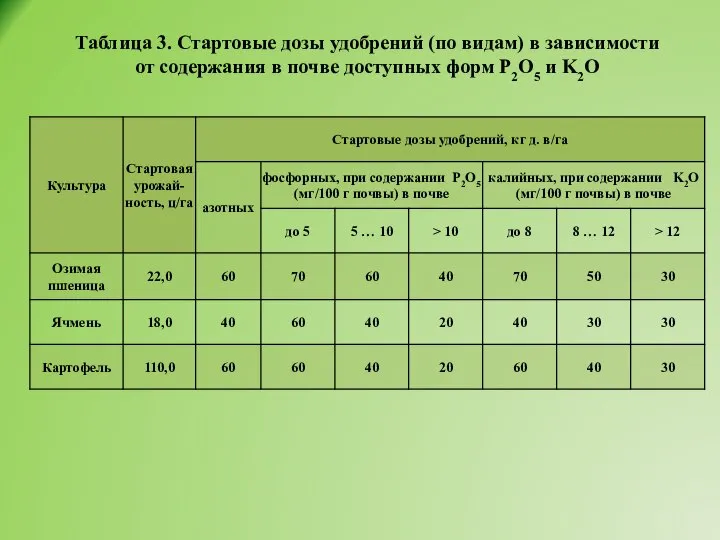
- 7. Таблица 3. Стартовые дозы удобрений (по видам) в зависимости от содержания в почве доступных форм P2O5
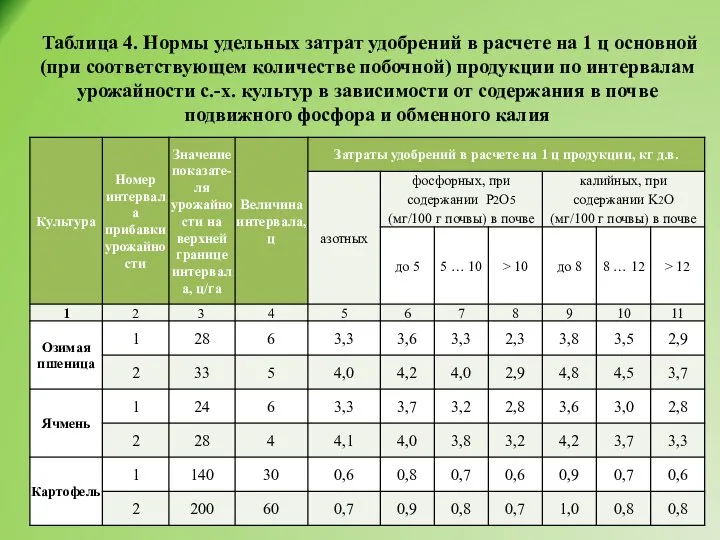
- 8. Таблица 4. Нормы удельных затрат удобрений в расчете на 1 ц основной (при соответствующем количестве побочной)
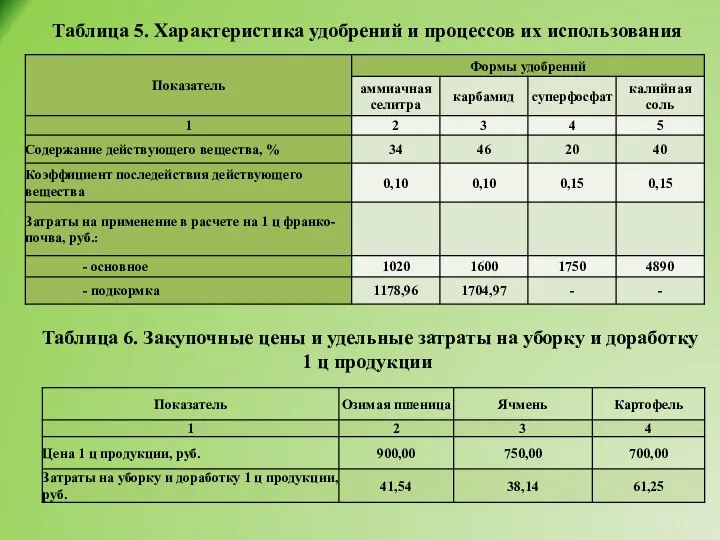
- 9. Таблица 5. Характеристика удобрений и процессов их использования Таблица 6. Закупочные цены и удельные затраты на
- 10. Разработка экономико-математической модели (вариант 1) Система переменных экономико-математической модели Участок № 1 х1, х2, х3 –
- 11. Система переменных экономико-математической модели Участок № 2 х16, х17, х18 – дозы действующего вещества, соответственно N,
- 12. Система ограничений экономико-математической модели 1.Группа ограничений по балансу выноса элементов питания продукцией и внесения их с
- 13. Система ограничений экономико-математической модели Ограничения по затратам действующего вещества удобрений в первом интервале прибавки урожайности озимой
- 14. Система ограничений экономико-математической модели Ограничения по затратам действующего вещества удобрений в первом интервале прибавки урожайности картофеля:
- 15. Система ограничений экономико-математической модели 2. Группа ограничений по границе интервалов прибавки урожайности Обобщенная математическая запись ограничений
- 16. Система ограничений экономико-математической модели По величине первого интервала прибавки урожайности озимой пшеницы (4): х4 ≤ 6;
- 17. Система ограничений экономико-математической модели 3. Группа ограничений по формированию годовых норм удобрений в ассортименте поставки Обобщенная
- 18. Система ограничений экономико-математической модели По формированию доз азотных удобрений (аммиачной селитры и карбамида) для внесения под
- 19. Система ограничений экономико-математической модели 4. Группа ограничений по распределению годовых удобрений по срокам внесения Обобщенная математическая
- 20. Система ограничений экономико-математической модели По распределению годовых норм аммиачной селитры и карбамида под зерновые (озимая пшеница)
- 21. Система ограничений экономико-математической модели 5. Группа ограничений по допустимому удельному весу отдельных форм удобрений в общей
- 22. Система ограничений экономико-математической модели По удельному весу карбамида в дозе азотных удобрений, вносимой под зерновые в
- 23. Система ограничений экономико-математической модели 6. Группа ограничений по суммарному приросту урожайности на участке Обобщенная математическая запись
- 24. По суммарному приросту урожайности озимой пшеницы (14): х4 + х8 = х15; х4 + х8 –
- 25. Система ограничений экономико-математической модели 7. Группа ограничений по балансу ресурсов и потребления удобрений Обобщенная математическая запись
- 26. Система ограничений экономико-математической модели По фонду аммиачной селитры, тонн физической массы (29): 0,1(60(х9 + х13) +
- 27. Система ограничений экономико-математической модели 8. Группа ограничений по производству продукции Обобщенная математическая запись ограничений данной группы:
- 28. Система ограничений экономико-математической модели По приросту производства зерна, т (33): 0,1·60·х15 ≥ 42; 6·х15 ≥ 42;
- 29. Условия неотрицательности переменных экономико-математической модели
- 30. Целевая функция экономико-математической модели В качестве критерия оптимальности использован показатель дополнительного чистого дохода, отнесенного на удобрение.
- 31. Целевая функция имеет вид: max z = –61200х9 – 96000х10 –105000х11 – – 293400х12 – 70737,6х13
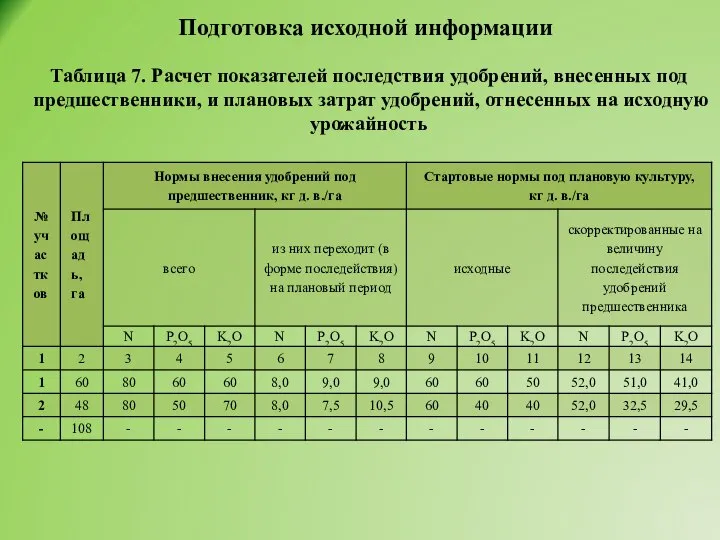
- 32. Подготовка исходной информации Таблица 7. Расчет показателей последствия удобрений, внесенных под предшественники, и плановых затрат удобрений,
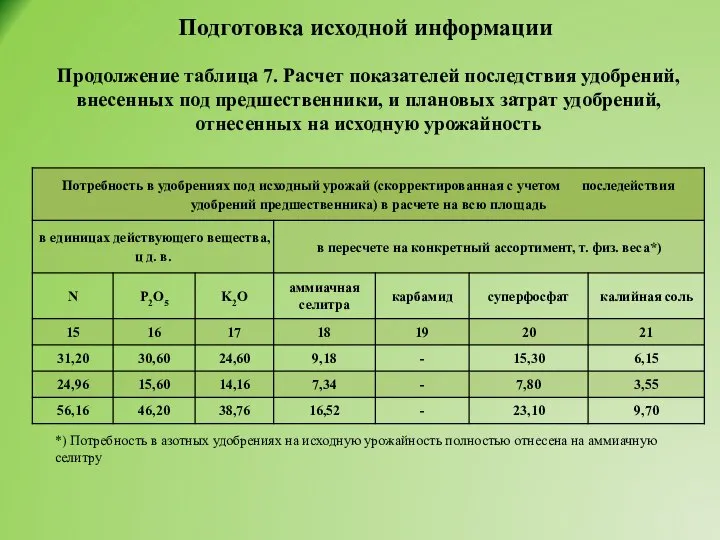
- 33. Подготовка исходной информации Продолжение таблица 7. Расчет показателей последствия удобрений, внесенных под предшественники, и плановых затрат
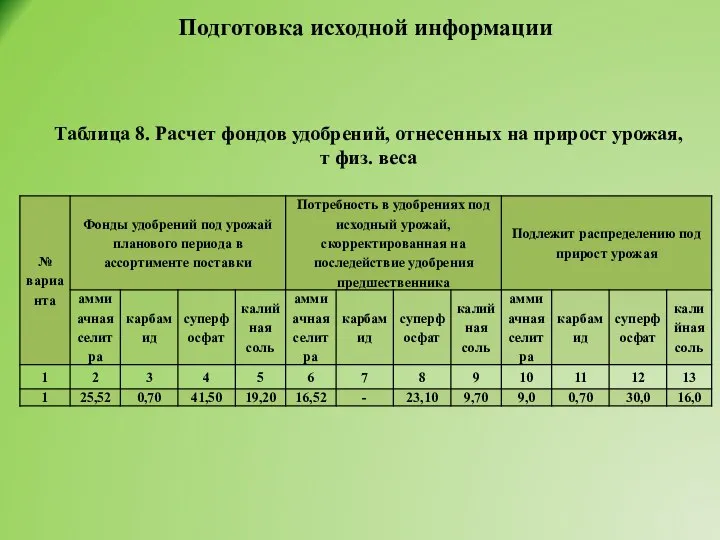
- 34. Подготовка исходной информации Таблица 8. Расчет фондов удобрений, отнесенных на прирост урожая, т физ. веса
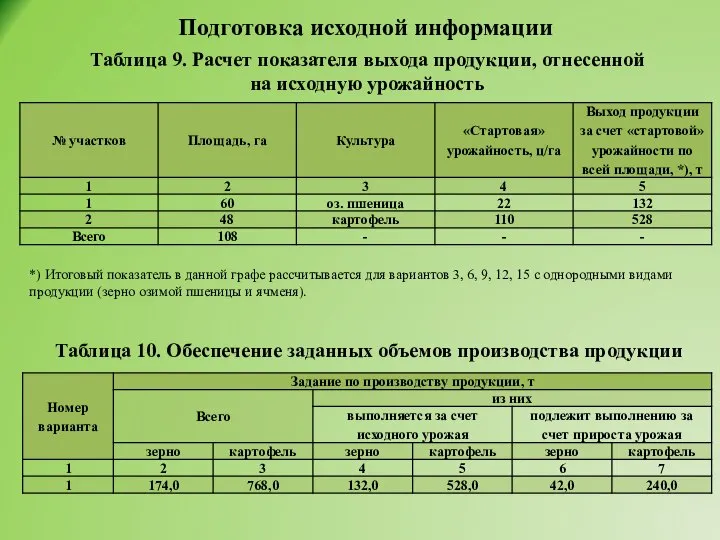
- 35. Подготовка исходной информации Таблица 9. Расчет показателя выхода продукции, отнесенной на исходную урожайность *) Итоговый показатель
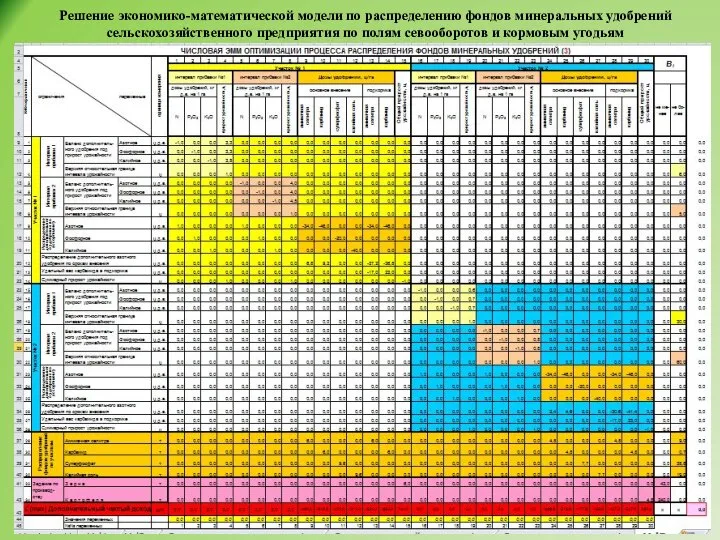
- 36. Решение экономико-математической модели по распределению фондов минеральных удобрений сельскохозяйственного предприятия по полям севооборотов и кормовым угодьям
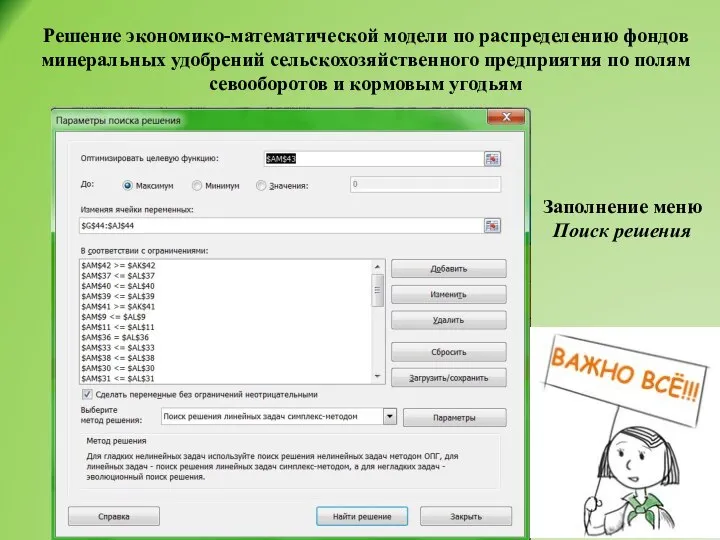
- 37. Решение экономико-математической модели по распределению фондов минеральных удобрений сельскохозяйственного предприятия по полям севооборотов и кормовым угодьям
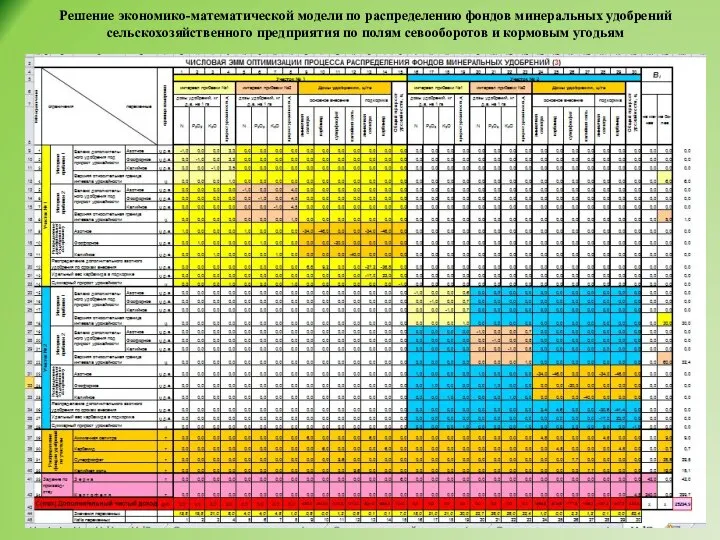
- 38. Решение экономико-математической модели по распределению фондов минеральных удобрений сельскохозяйственного предприятия по полям севооборотов и кормовым угодьям
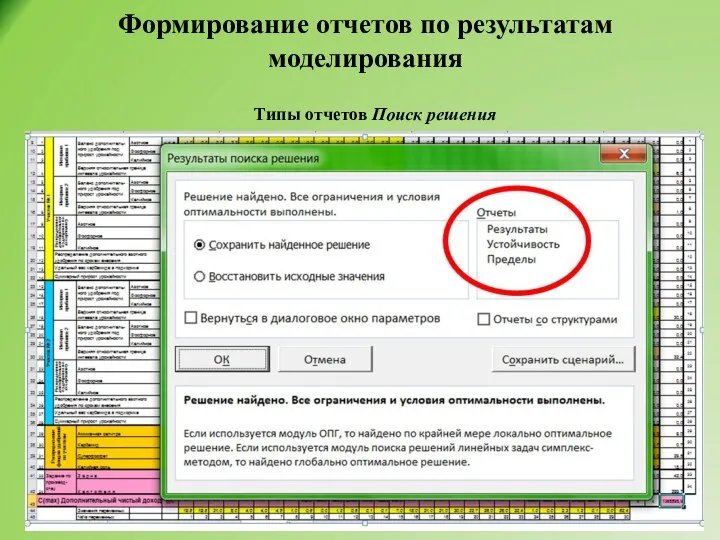
- 39. Формирование отчетов по результатам моделирования Типы отчетов Поиск решения
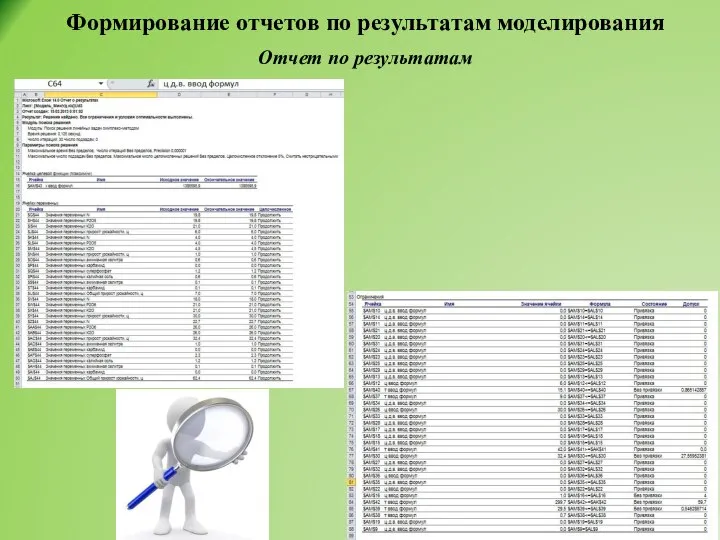
- 40. Формирование отчетов по результатам моделирования Отчет по результатам
- 41. Формирование отчетов по результатам моделирования Отчет по устойчивости ФОКУС ВНИМАНИЯ
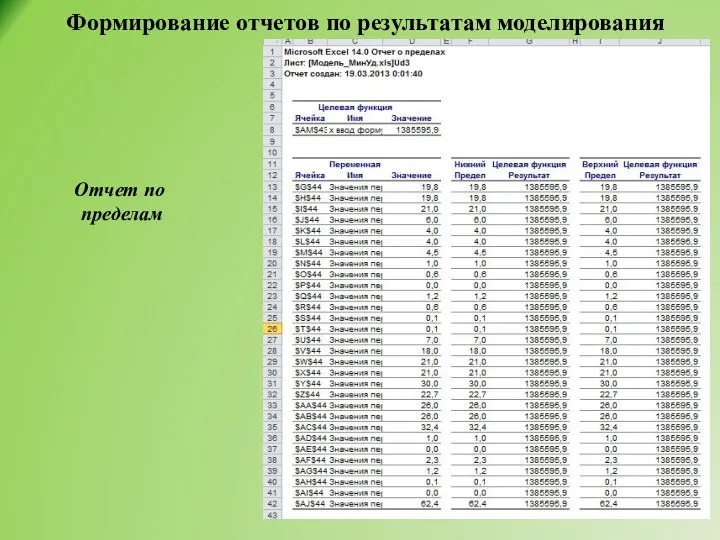
- 42. Формирование отчетов по результатам моделирования Отчет по пределам
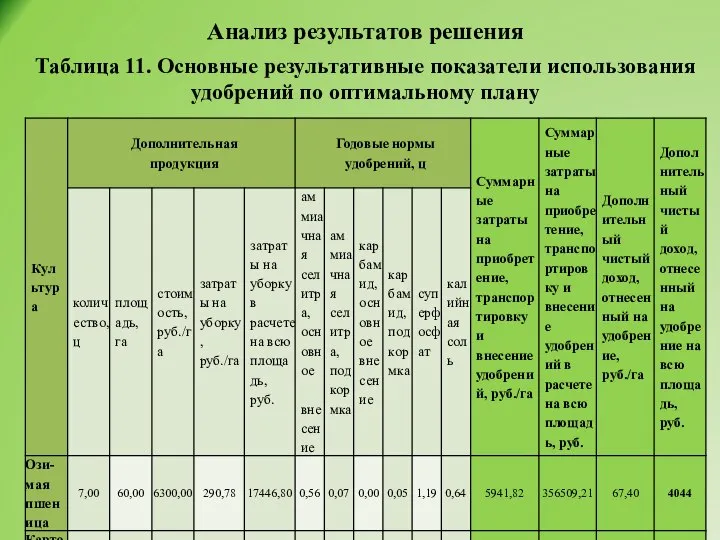
- 43. Анализ результатов решения Таблица 11. Основные результативные показатели использования удобрений по оптимальному плану
- 44. Анализ результатов решения Размер дополнительного чистого дохода от применения удобрений под прирост урожая составляет 1385,6 тыс.
- 46. Скачать презентацию



























 Правовое обеспечение экономики, экономической деятельности, экономической безопасности
Правовое обеспечение экономики, экономической деятельности, экономической безопасности Статистика научно-технического прогресса
Статистика научно-технического прогресса Кривая Филлипса
Кривая Филлипса Цели и виды фискальной политики
Цели и виды фискальной политики Экономическая система и ее виды
Экономическая система и ее виды Румыния - социально-экономическая характеристика страны
Румыния - социально-экономическая характеристика страны Экономическая активность
Экономическая активность Week 6 & 7: Trade and the Environment (Ch.13)
Week 6 & 7: Trade and the Environment (Ch.13) Экономика Л-19 КР
Экономика Л-19 КР Крупнейшие производители. Крупнейшие экспортеры
Крупнейшие производители. Крупнейшие экспортеры Платежный баланс Российской Федерации Сударкина Анастасия, Назаренко Александра ДС.01
Платежный баланс Российской Федерации Сударкина Анастасия, Назаренко Александра ДС.01 Экономика. Сделки
Экономика. Сделки Креативная экономика
Креативная экономика Экономика. Экономические системы
Экономика. Экономические системы Основы организации деятельности предприятия
Основы организации деятельности предприятия Принцип спроса и предложения
Принцип спроса и предложения Что такое хозяйство страны?
Что такое хозяйство страны? Альфред Маршалл та його внесок у світову економічну науку
Альфред Маршалл та його внесок у світову економічну науку Анализ финансовых результатов деятельности предприятия участника ВЭД Подготовила: Клеутина Светлана Группа МЭ-092
Анализ финансовых результатов деятельности предприятия участника ВЭД Подготовила: Клеутина Светлана Группа МЭ-092 Цена и ценообразование
Цена и ценообразование Трастовые и депозитарные операции коммерческих банков Выполнила: Гудимова К.С., Студентка группы МЭ091, ДС1
Трастовые и депозитарные операции коммерческих банков Выполнила: Гудимова К.С., Студентка группы МЭ091, ДС1 Ресурсы. Факторы производства. Задание для выполнения
Ресурсы. Факторы производства. Задание для выполнения Экономическая система: сущность, структура, функции, производственные возможности
Экономическая система: сущность, структура, функции, производственные возможности Система цен в современной экономике
Система цен в современной экономике Урок налоговой грамотности
Урок налоговой грамотности Теория экономического роста
Теория экономического роста Конкурентоспособность ЧТУП Руд Буд
Конкурентоспособность ЧТУП Руд Буд Виды, причины и последствия инфляции
Виды, причины и последствия инфляции