Содержание
- 2. Логика и язык Знак — это материальный предмет (явление, событие), выступающий в качестве представителя некоторого другого
- 3. Каждое имя имеет значение и смысл. Значением имени является обозначаемый им предмет. Смысл (или концепт) имени
- 4. Соотношение трех понятий: «имя», «значение», «смысл» — схематически можно выразить таким образом:
- 5. Именная функция Именная функция — это выражение, которое при замене переменных постоянными превращается в обозначение предмета.
- 6. Пропозициональная функция Пропозициональной функцией называется выражение, содержащее переменную и превращающееся в истинное или ложное высказывание при
- 7. Семантические категории Выражения (слова и словосочетания) естественного языка, имеющие какой-либо самостоятельный смысл, можно разбить на так
- 8. логические термины (логические постоянные, или логические константы). В естественном языке имеются слова и словосочетания: «и», «или»,
- 9. Конъюнкция соответствует союзу «и». Конъюнктивное высказывание обозначается: а b, или а •b, или a b (например,
- 10. Квантор общности обозначается и соответствует кванторным словам «все» («всякий», «каждый», «ни один»). (Например, в суждении «Все
- 11. Разновидности семантических категорий
- 12. Понятие — это форма мышления, в которой отражаются существенные признаки одноэлементного класса или класса однородных предметов.
- 13. Понятие формируется на основе обобщения существенных признаков (т.е. свойств и отношений), присущих ряду однородных предметов. Для
- 14. Основными логическими приемами формирования понятий являются. Анализ — мысленное расчленение предметов на их составные части, мысленное
- 15. Содержанием понятия называется совокупность существенных признаков одноэлементного класса или класса однородных предметов, отраженных в этом понятии.
- 17. Игрушка, заводная игрушка, кукла, заводной автомобиль, пистолет
- 19. Скачать презентацию
Слайд 2Логика и язык
Знак — это материальный предмет (явление, событие), выступающий в качестве
Логика и язык
Знак — это материальный предмет (явление, событие), выступающий в качестве

Знаки подразделяются на языковые и неязыковые. К неязыковым знакам относятся:
знаки-копии (например, фотографии, отпечатки пальцев, репродукции и т.д.),
знаки-признаки, или знаки-показатели (например, дым — признак огня, повышенная температура тела — признак болезни),
знаки-сигналы (например, звонок — знак начала или окончания занятия),
знаки-символы (например, дорожные знаки) и другие виды знаков.
Разновидностями знаков являются языковые знаки, использующиеся в вышеперечисленных функциях. Одна из важнейших функций языковых знаков состоит в обозначении ими предметов. Для обозначения предметов служат имена.
Имя — это слово или словосочетание, обозначающее какой-либо определенный предмет. (Слова «обозначение», «именование», «название» рассматриваются как синонимы).
Предмет здесь понимается в весьма широком смысле: это вещи, свойства, отношения, процессы, явления и т.п. как природы, так и общественной жизни, психической деятельности людей, продукты их воображения и результаты абстрактного мышления. Итак, имя всегда есть имя некоторого предмета. Хотя предметы изменчивы, текучи, в них сохраняется качественная определенность, которую и обозначает имя данного предмета.
Слайд 3Каждое имя имеет значение и смысл. Значением имени является обозначаемый им предмет.
Каждое имя имеет значение и смысл. Значением имени является обозначаемый им предмет.

Вместо слова «значение» в логической литературе употребляют другие (тождествен¬ные, си-нонимические) названия: чаще всего «денотат», иногда «десигнат», «номинат» или «референт».
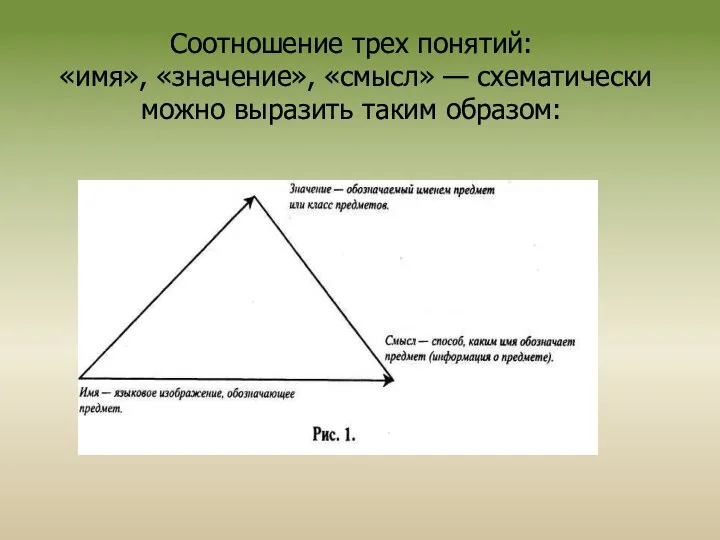
Слайд 4Соотношение трех понятий:
«имя», «значение», «смысл» — схематически можно выразить таким образом:
Соотношение трех понятий:
«имя», «значение», «смысл» — схематически можно выразить таким образом:
Слайд 5Именная функция
Именная функция — это выражение, которое при замене переменных постоянными превращается
Именная функция
Именная функция — это выражение, которое при замене переменных постоянными превращается

«отец у». Поставив вместо у имя «писатель Жюль Верн»
получим «отец писателя Жюля Верна» —
имя предмета (в данном случае — имя человека).
Именная функция — это такое выражение, которое не является непосредственно именем ни для какого предмета и нуждается в некотором восполнении для того, чтобы стать именем предмета.
Так, выражение х2 — 1 не обозначает никакого предмета, но если мы его «восполним», поставив, например, на место х имя числа 3 (обозначающее это число цифру), то получим выражение
З2 — 1, которое является уже именем для числа 8, т.е. для некоторого предмета.
Аналогично выражение х2 + у2 не обозначает никакого предмета, но при подстановке на место х и у каких-нибудь имен чисел, например «4» и «1», превращается в имя числа 17. Такие нуждающиеся в восполнении выражения, как х2 — 1, х2 + у2, и называют функциями — первая от одного, вторая от двух аргументов.
Слайд 6Пропозициональная функция
Пропозициональной функцией называется выражение, содержащее переменную и превращающееся в истинное или
Пропозициональная функция
Пропозициональной функцией называется выражение, содержащее переменную и превращающееся в истинное или

Приведем примеры пропозициональных функций: «z — город»: «х — советский космонавт»; «у — четное число»; «х + у = 10»; «х3 — 1 = 124».
Пропозициональные функции делятся на одноместные, содержащие одну переменную, называемые свойствами (например, «х — композитор», «x-7 = 3», «z— гвоздика»), и содержащие две и более переменных, называемые отношениями (например, «х > у»\ «х — z = 16»; «объем куба х равен объему куба у»).
Возьмем в качестве примера пропозициональную функцию «х — нечетное число» и, подставив вместо х число 4, получим высказывание «4 — нечетное число», которое ложно, а подставив число 5, получим истинное высказывание «5 — нечетное число».
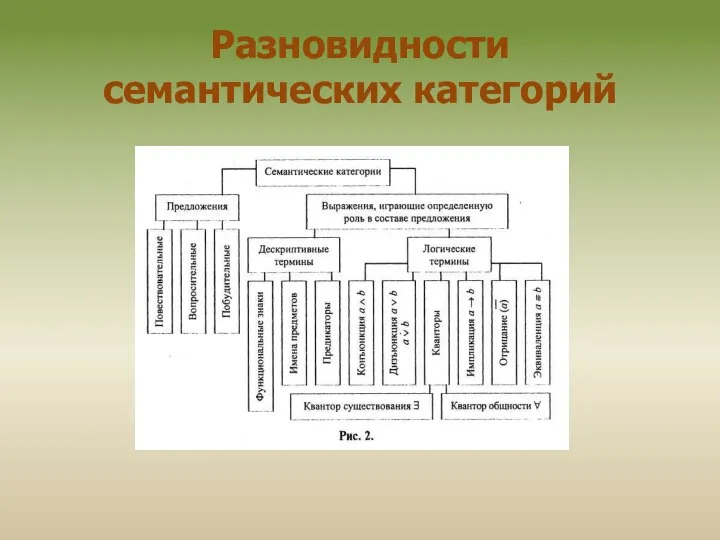
Слайд 7Семантические категории
Выражения (слова и словосочетания) естественного языка, имеющие какой-либо самостоятельный смысл, можно
Семантические категории
Выражения (слова и словосочетания) естественного языка, имеющие какой-либо самостоятельный смысл, можно

к ним относятся: 1) предложения: повествовательные, побудительные, вопросительные;
2) дескриптивные и логические термины (выражения, играющие определенную роль в составе предложений)
К дескриптивным (описательным) терминам относятся:
1.Имена предметов — слова или словосочетания, обозначающие единичные (материальные или идеальные) предметы («Аристотель», «первый космонавт», «7») или классы однородных предметов (например, «пароход», «книга», «стихотворение», «засуха», «гвардейский полк» и др.).
2. Предикаторы - (знаки предметно-пропозициональных функций) — слова и словосочетания, обозначающие свойства предметов или отношения между предметами
(например, «порядочный», «синий», «электропроводный», «есть город», «меньше», «есть число», «есть планета» и др.).
Предикаторы бывают одноместные и многоместные.
Одноместные предикаторы обозначают свойства (например, «талантливый», «горький», «большой»).
Многоместные предикаторы обозначают (выражают) отношения. Двухместными предикаторами являются: «равен», «больше», «мать», «помнит» и др.
Например: «Площадь земельного участка А равна площади земельного участка В», «Мария Васильевна — мать Сережи».
Пример трехместного предикатора — «между» (например: «Город Москва расположен между городами Санкт-Петербург и Ростов-на-Дону»).
«Енисей — река Сибири» встречаются три имени предмета: «Енисей», «река», «Сибирь». Имя предмета «Енисей» выполняет роль субъекта, а имена «река» и «Сибирь» входят в предикат («река Сибири») как его две составные части.
3.Функциональные знаки (знаки именных функций) — выражения, обозначающие предметные функции, операции («ctg a», «+», «/» и др.).
Слайд 8логические термины (логические постоянные, или логические константы).
В естественном языке имеются слова и
логические термины (логические постоянные, или логические константы).
В естественном языке имеются слова и

В символической (или математической) логике в качестве таких констант обычно используются
конъюнкция, дизъюнкция, отрицание, импликация, эквиваленция, кванторы общности и существования и некоторые другие.
В символической логике логические термины (логические постоянные) записываются следующим образом:
Слайд 9Конъюнкция соответствует союзу «и». Конъюнктивное высказывание обозначается: а b, или а •b,
Конъюнкция соответствует союзу «и». Конъюнктивное высказывание обозначается: а b, или а •b,

(например, «Закончились лекции (а), и студенты пошли домой (b)».
Дизъюнкция соответствует союзу «или». Дизъюнктивное суждение обозначается:
a b (нестрогая дизъюнкция) и a b (строгая дизъюнкция); отличие их в том, что при строгой дизъюнкции сложное суждение истинно только в том случае, когда истинно одно из составляющих суждений, но не оба, а при нестрогой дизъюнкции истинными могут быть одновременно оба суждения. «Он шахматист или футболист» обозначается как а b.
«Сейчас Петров находится дома или в институте» обозначается как а b.
Импликация соответствует союзу «если... то». Условное суждение обозначается: а b, или а b (например: «Если будет хорошая погода, то мы пойдем в лес»).
Эквиваленция соответствует словам «если и только если», «тогда и только тогда, когда», «эквивалентно». Эквивалентное высказывание обозначается: а b, или , или
Отрицание соответствует словам «не», «неверно, что». Отрицание высказывания обозначается: [например: «Падает снег» (а); «Неверно, что падает снег» .
Здесь и в дальнейшем буквами a,b, с и т.д. обозначаются переменные высказывания (суждения).
Слайд 10Квантор общности обозначается и соответствует кванторным словам «все» («всякий», «каждый», «ни один»).
Квантор общности обозначается и соответствует кванторным словам «все» («всякий», «каждый», «ни один»).

Квантор существования обозначается и соответствует словам «некоторые», «существует».
(Например, в суждениях «Некоторые люди имеют высшее образование» или «Существуют люди, которые имеют высшее образование» — кванторные слова выделены курсивом).
Слайд 11Разновидности
семантических категорий
Разновидности
семантических категорий
Слайд 12Понятие — это форма мышления, в которой отражаются существенные признаки одноэлементного класса
Понятие — это форма мышления, в которой отражаются существенные признаки одноэлементного класса

Слайд 13Понятие формируется на основе обобщения существенных признаков (т.е. свойств и отношений), присущих
Понятие формируется на основе обобщения существенных признаков (т.е. свойств и отношений), присущих

Для выделения существенных признаков необходимо абстрагироваться (отвлечься) от несущественных, которых в любом предмете очень много. Этому помогает сравнение, сопоставление предметов.
Для выделения ряда признаков требуется произвести анализ, т.е. мысленно расчленить целый предмет на его составные части, элементы, стороны, отдельные признаки.
Обратная операция — синтез (мысленное объединение) частей предмета, отдельных признаков, притом признаков существенных, в единое целое. Мысленному анализу как приему, используемому при образовании понятий, часто предшествует анализ практический, т.е. разложение, расчленение предмета на его составные части. Мысленному синтезу предшествует практический сбор частей предмета в единое целое с учетом правильного взаимного расположения частей при сборке.
Слайд 14Основными логическими приемами формирования понятий являются.
Анализ — мысленное расчленение предметов на их
Основными логическими приемами формирования понятий являются.
Анализ — мысленное расчленение предметов на их

Синтез — мысленное соединение в единое целое частей предмета или его признаков, полученных в процессе анализа.
Сравнение — мысленное установление сходства или различия предметов по существенным или несущественным признакам.
Абстрагирование — мысленное выделение одних признаков предмета и отвлечение от других. Часто задача состоит в выделении существенных признаков и в отвлечении от несущественных, второстепенных.
Обобщение — мысленное объединение однородных предметов в некоторый класс.
Слайд 15Содержанием понятия называется совокупность существенных признаков одноэлементного класса или класса однородных предметов,
Содержанием понятия называется совокупность существенных признаков одноэлементного класса или класса однородных предметов,

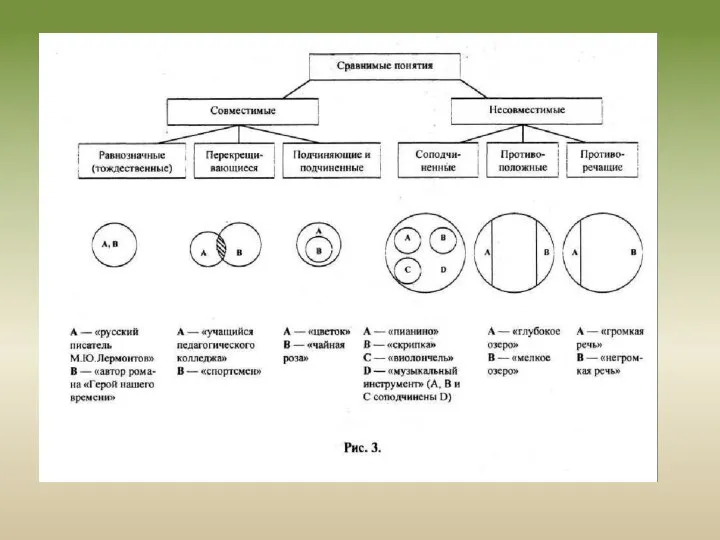
Объемом понятия называют совокупность (класс) предметов, которая мыслится в понятии. Объективно, т.е. вне сознания человека, существуют различные предметы, например, школьники. Под объемом понятия «школьник» подразумевается множество всех школьников, которые существуют сейчас, существовали ранее и будут существовать в будущем. Класс (или множество) состоит из отдельных объектов, которые называются его элементами. В зависимости от их числа множества делятся на конечные и бесконечные.
Например, множество столиц государств конечно, а множество натуральных чисел бесконечно. Множество (класс) А называется подмножеством (подклассом) множества (класса) В, если каждый элемент А является элементом В. Такое отношение между подмножеством А и множеством В называется отношением включения класса А в класс В и записывается так: . Читается: класс А входит в класс В. Это отношение вида и рода (например, класс «стол» входит в класс «мебель»).
Читается: элемент а принадлежит классу А. Например, а — «Нева» и А — «река».
Классы А и В являются тождественными (совпадающими), если и , что
Слайд 17Игрушка, заводная игрушка, кукла, заводной автомобиль, пистолет
Игрушка, заводная игрушка, кукла, заводной автомобиль, пистолет

 Мои размышления. Схема мироздания в твоих глазах
Мои размышления. Схема мироздания в твоих глазах Древнегреческие ученые Эмпидокл и Зенон
Древнегреческие ученые Эмпидокл и Зенон Философия науки
Философия науки Новое время
Новое время Западноевропейская философская мысль в Новое время и эпоху Просвещения
Западноевропейская философская мысль в Новое время и эпоху Просвещения Эволюция представлений об окружающем мире
Эволюция представлений об окружающем мире Становление мифологии из философии
Становление мифологии из философии Сущность и происхождение этики. Основы деловой этики. Лекция 1
Сущность и происхождение этики. Основы деловой этики. Лекция 1 Нравственные основы службы в органах внутренних дел Российской Федерации
Нравственные основы службы в органах внутренних дел Российской Федерации Современные логики. Классическое и неклассическое в логике. Тема 6
Современные логики. Классическое и неклассическое в логике. Тема 6 Пессимизм
Пессимизм Тема №4 Средневековая философия Запада и Востока
Тема №4 Средневековая философия Запада и Востока Выполнила: Кахарова Наргиза Факультет: ОМ Группа: 029/2
Выполнила: Кахарова Наргиза Факультет: ОМ Группа: 029/2 Деистическое направление философии французского Просвещения XVIII века
Деистическое направление философии французского Просвещения XVIII века Мировоззрение
Мировоззрение Смысл жизни человека
Смысл жизни человека Проблема сознания в философии и науке ХХ века
Проблема сознания в философии и науке ХХ века Методология. Разработка гипотезы и концепции исследования
Методология. Разработка гипотезы и концепции исследования Моральный выбор – это ответственность
Моральный выбор – это ответственность Педагогические идеи Д. Локка и Ж.Ж. Руссо
Педагогические идеи Д. Локка и Ж.Ж. Руссо Навыки написания эссе
Навыки написания эссе Философия эпохи возрождения
Философия эпохи возрождения Латинские синтеции В мире мудрых мыслей
Латинские синтеции В мире мудрых мыслей Философия Нового времени (продолжение)
Философия Нового времени (продолжение) Философия Картины мира
Философия Картины мира Немецкая классическая философия и её значение
Немецкая классическая философия и её значение Высказывания о жизни
Высказывания о жизни Философия и образование. Феномен повседневности в философской практике
Философия и образование. Феномен повседневности в философской практике