Содержание
- 2. Содержание 1. Основные теоретические сведения: последовательное, параллельное, смешанное соединения резисторов, сопротивление всей цепи. 2. Практическое задание:
- 3. Основные теоретические сведения Постоянным называется электрический ток, не изменяющийся во времени. Продолжить
- 4. Резистором называется элемент электрической цепи, предназначенный для использования его электрического сопротивления. Условные графические обозначения: - резистор
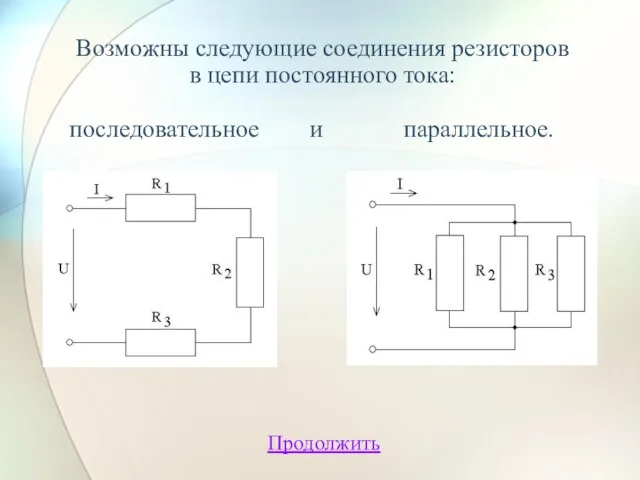
- 5. Возможны следующие соединения резисторов в цепи постоянного тока: последовательное и параллельное. Продолжить
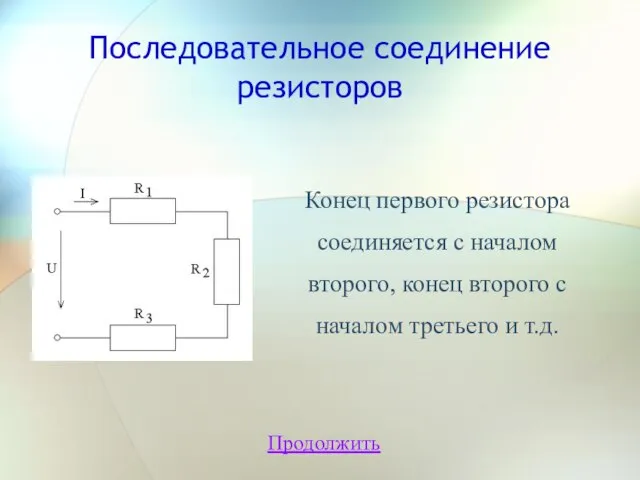
- 6. Последовательное соединение резисторов Продолжить Конец первого резистора соединяется с началом второго, конец второго с началом третьего
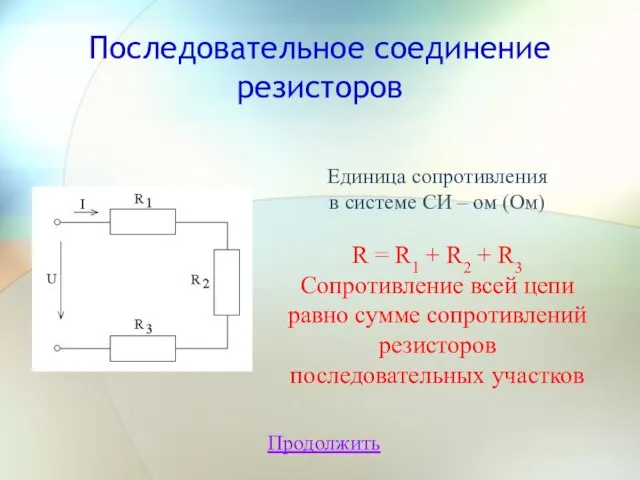
- 7. Последовательное соединение резисторов Продолжить Единица сопротивления в системе СИ – ом (Ом) R = R1 +
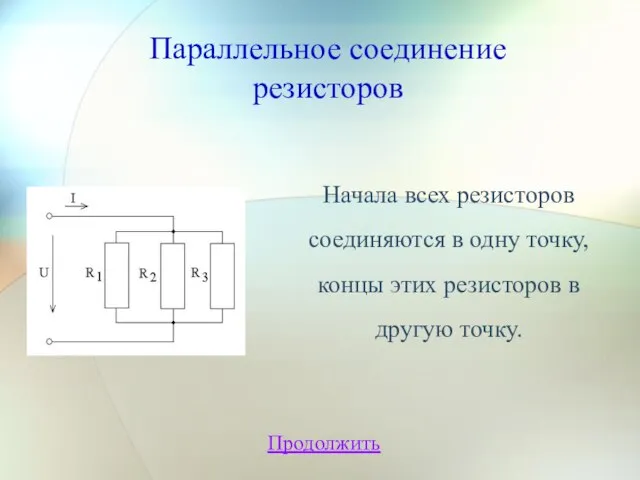
- 8. Параллельное соединение резисторов Продолжить Начала всех резисторов соединяются в одну точку, концы этих резисторов в другую
- 9. Параллельное соединение резисторов Продолжить Величина, обратная сопротивлению, называется проводимостью G = 1/R Единица проводимости в системе
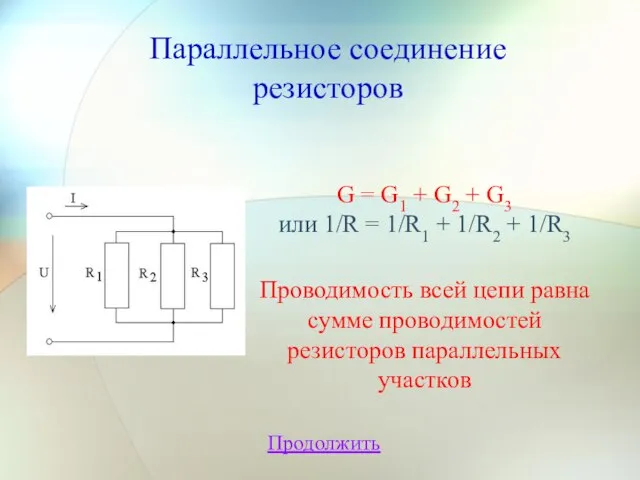
- 10. Параллельное соединение резисторов Продолжить G = G1 + G2 + G3 или 1/R = 1/R1 +
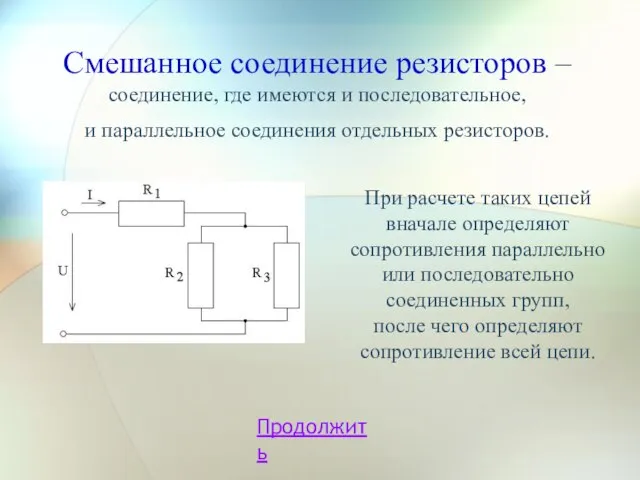
- 11. Смешанное соединение резисторов – соединение, где имеются и последовательное, и параллельное соединения отдельных резисторов. Продолжить При
- 12. Продолжить Преобразование треугольника в звезду Такое преобразование применяется при расчетах сложных цепей постоянного тока и цепей
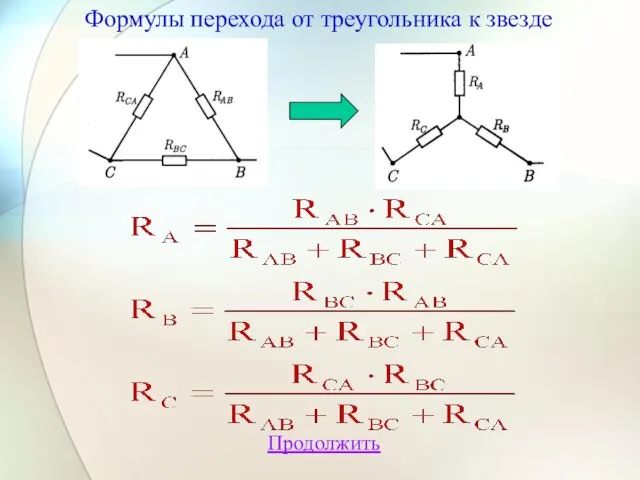
- 13. Продолжить Формулы перехода от треугольника к звезде
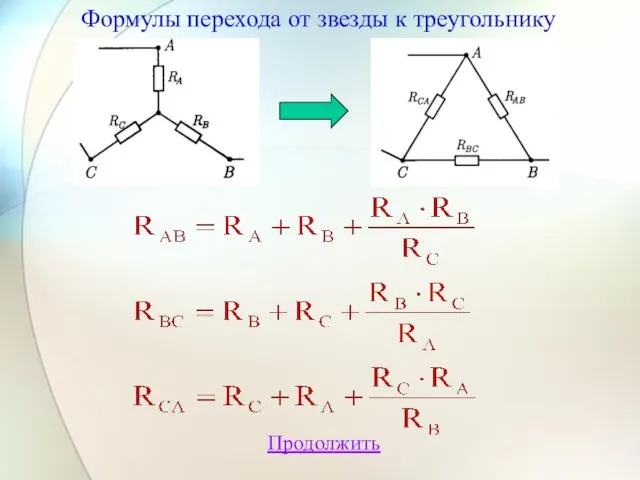
- 14. Продолжить Формулы перехода от звезды к треугольнику
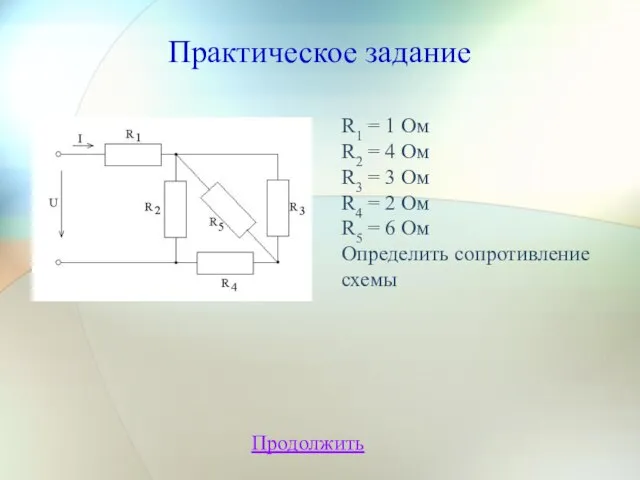
- 15. Практическое задание Продолжить R1 = 1 Ом R2 = 4 Ом R3 = 3 Ом R4
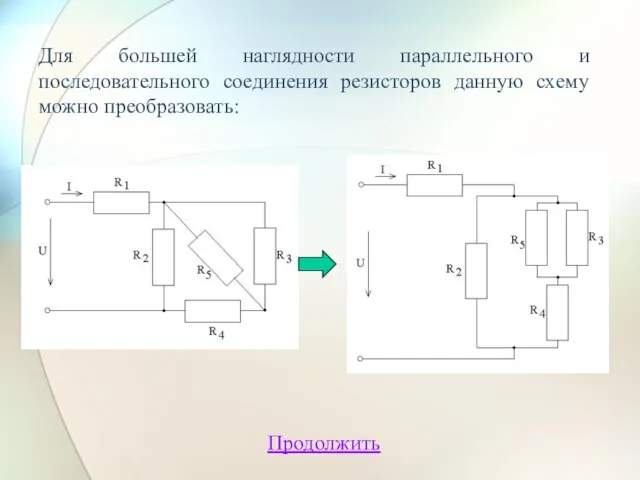
- 16. Для большей наглядности параллельного и последовательного соединения резисторов данную схему можно преобразовать: Продолжить
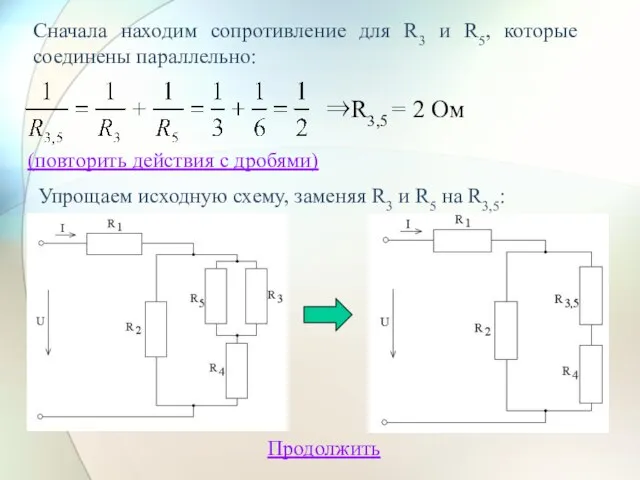
- 17. Сначала находим сопротивление для R3 и R5, которые соединены параллельно: ⇒R3,5 = 2 Ом Упрощаем исходную
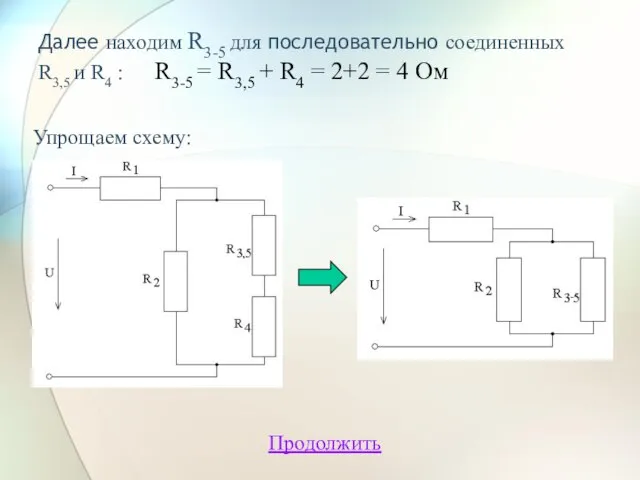
- 18. Далее находим R3-5 для последовательно соединенных R3,5 и R4 : R3-5 = R3,5 + R4 =
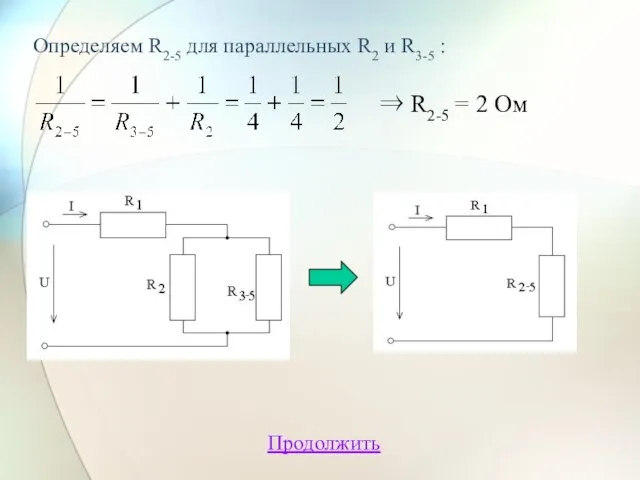
- 19. Определяем R2-5 для параллельных R2 и R3-5 : ⇒ R2-5 = 2 Ом Продолжить
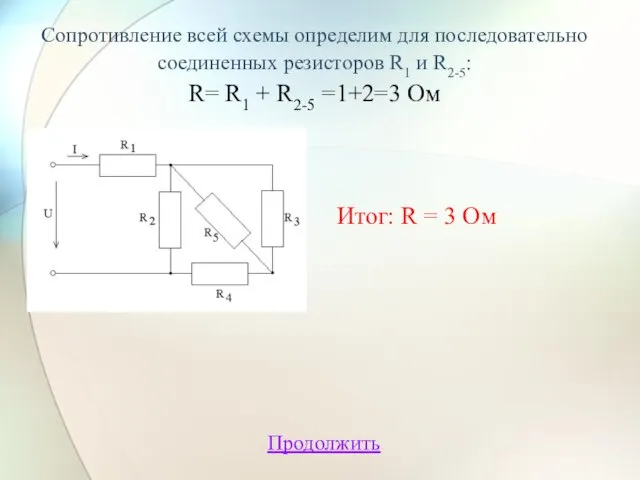
- 20. Сопротивление всей схемы определим для последовательно соединенных резисторов R1 и R2-5: R= R1 + R2-5 =1+2=3
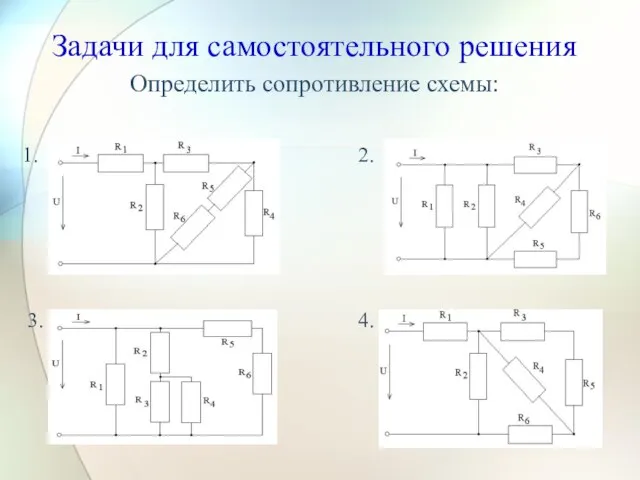
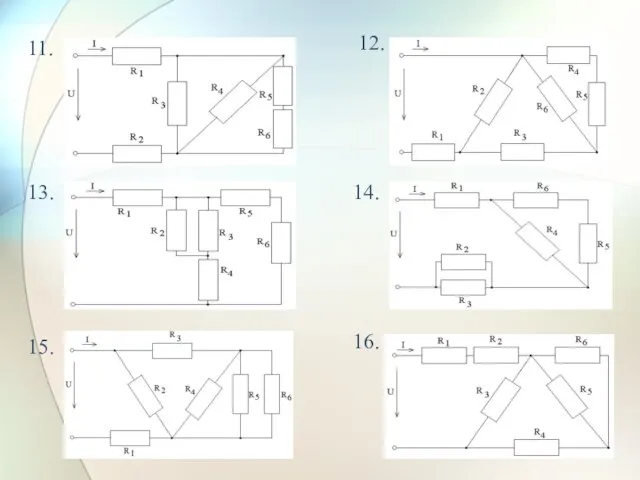
- 21. Задачи для самостоятельного решения Определить сопротивление схемы: 1. 2. 3. 4.
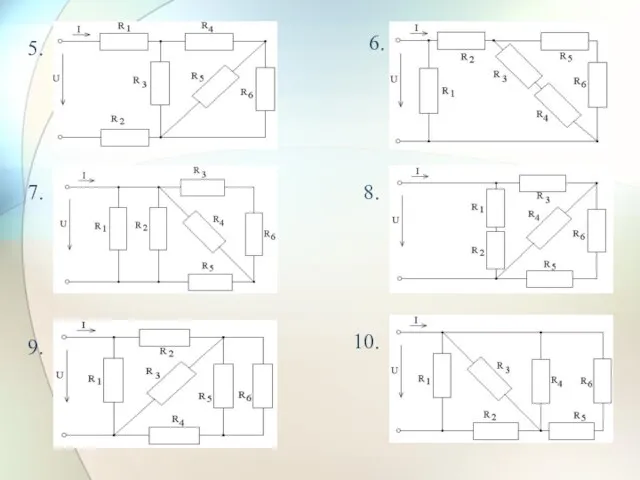
- 22. 7. 8. 9. 10. 5. 6.
- 23. 13. 14. 15. 16. 11. 12.
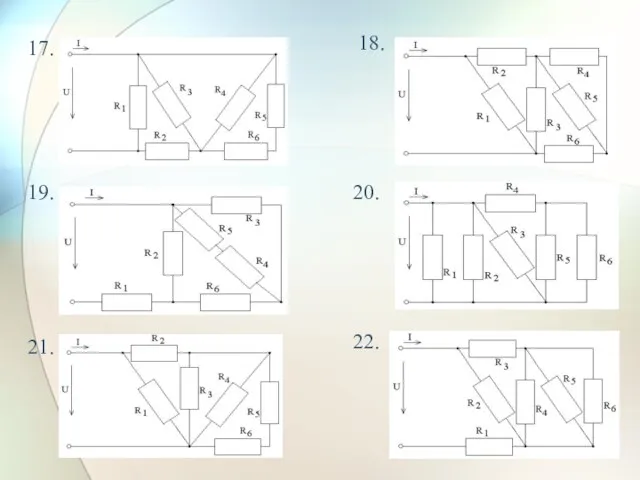
- 24. 19. 20. 21. 22. 17. 18.
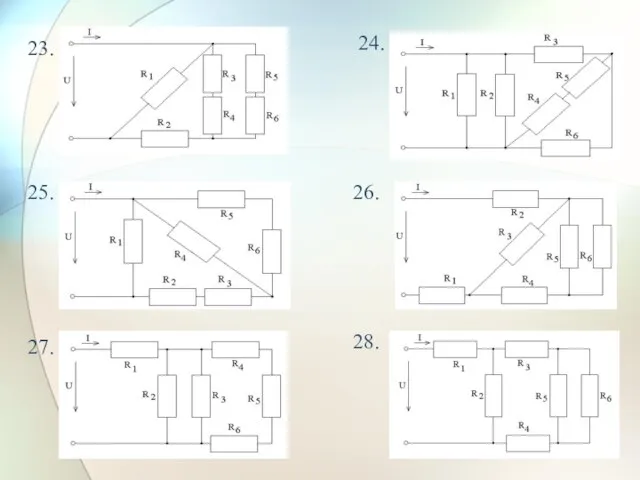
- 25. 25. 26. 27. 28. 23. 24.
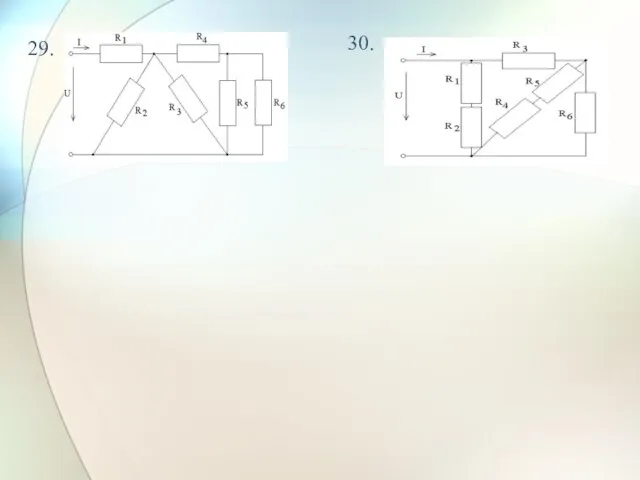
- 26. 29. 30.
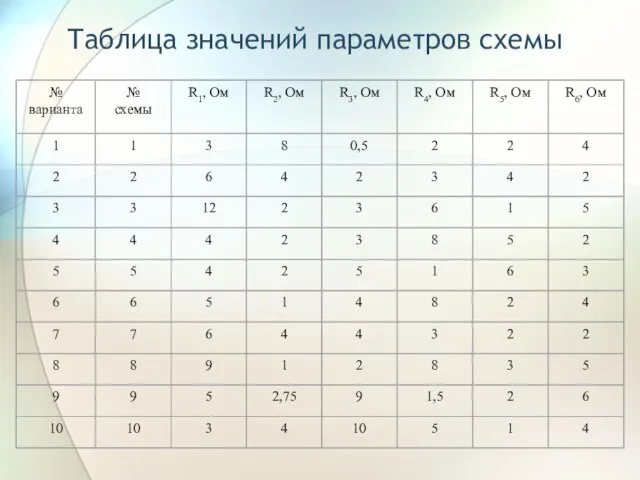
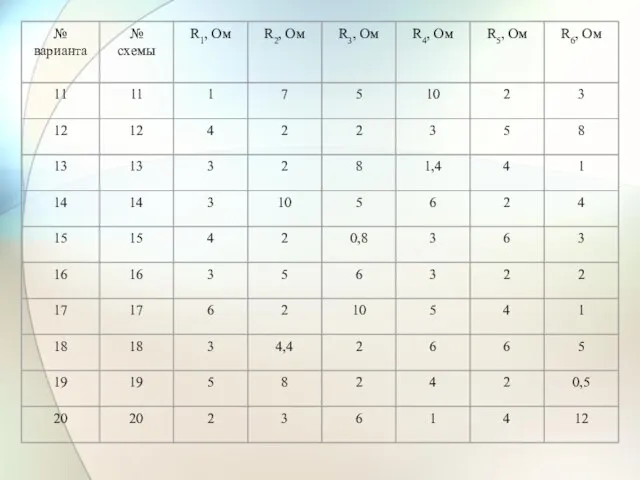
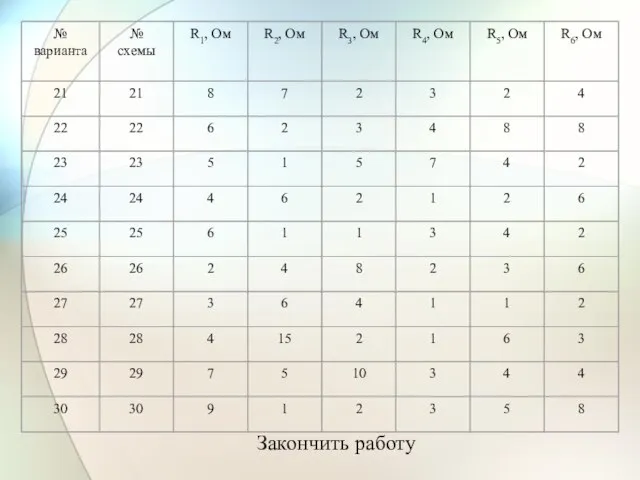
- 27. Таблица значений параметров схемы
- 29. Закончить работу
- 30. Действия с дробями Чтобы сложить (вычесть) дроби с разными знаменателями, необходимо: Шаг 1. Привести дроби к
- 31. Шаг 2. Находим дополнительные множители для дробей. Общий знаменатель делим на знаменатель каждой дроби: для первой
- 33. Скачать презентацию







 Механика. Гравитационные силы. Силы инерции
Механика. Гравитационные силы. Силы инерции Бином Ньютона
Бином Ньютона Активизации познавательной деятельности на уроке физики
Активизации познавательной деятельности на уроке физики Плотность вещества
Плотность вещества Технология ремонта подшипников скольжения
Технология ремонта подшипников скольжения Действие магнитного поля на движущийся заряд. Сила Лоренца
Действие магнитного поля на движущийся заряд. Сила Лоренца Антифрикционные материалы
Антифрикционные материалы Задачи на силу Архимеда
Задачи на силу Архимеда Исследование радиального профиля параметров активной среды лазеров с разрядом в полом катоде
Исследование радиального профиля параметров активной среды лазеров с разрядом в полом катоде Тест. Энергия
Тест. Энергия Электризация тел. Два рода зарядов. Проводники и диэлектрики
Электризация тел. Два рода зарядов. Проводники и диэлектрики Электромагнитные волны. Явления интерференции и дифракции
Электромагнитные волны. Явления интерференции и дифракции Вычисление силы тяжести
Вычисление силы тяжести Технологические характеристики грунтов. Определение трудности процессов разработки горных пород
Технологические характеристики грунтов. Определение трудности процессов разработки горных пород Магнитный поток
Магнитный поток 1.Силы, действующие в жикости. Режимы движения
1.Силы, действующие в жикости. Режимы движения Тепловые двигатели. История создания. Устройство. Принцип действия. КПД
Тепловые двигатели. История создания. Устройство. Принцип действия. КПД Решение задач. Последовательное соединение проводников
Решение задач. Последовательное соединение проводников Магнитное поле. Магнитостатика. Электромагнетизм
Магнитное поле. Магнитостатика. Электромагнетизм Презентация на тему Физика цвета
Презентация на тему Физика цвета  Влияние дефектов на физические свойства кристаллов
Влияние дефектов на физические свойства кристаллов Композиты и нанокомпозиты
Композиты и нанокомпозиты Масса. Измерение массы
Масса. Измерение массы Введение в специальность Квантовая метрология. Ядерные часы
Введение в специальность Квантовая метрология. Ядерные часы Характеристики электрического поля. Конденсаторы
Характеристики электрического поля. Конденсаторы Механические волны
Механические волны Светофор. Внеклассное мероприятие по физике
Светофор. Внеклассное мероприятие по физике Единая физическая картина мира
Единая физическая картина мира