Апертурные искажения. Форма и функция прозрачности развертывающего элемента

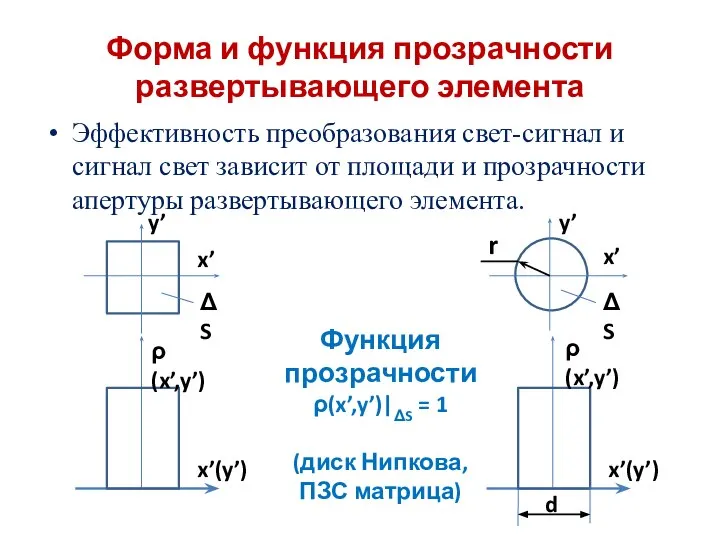
Форма и функция прозрачности развертывающего элемента
Эффективность преобразования свет-сигнал и сигнал свет зависит от площади и прозрачности апертуры развертывающего элемента.

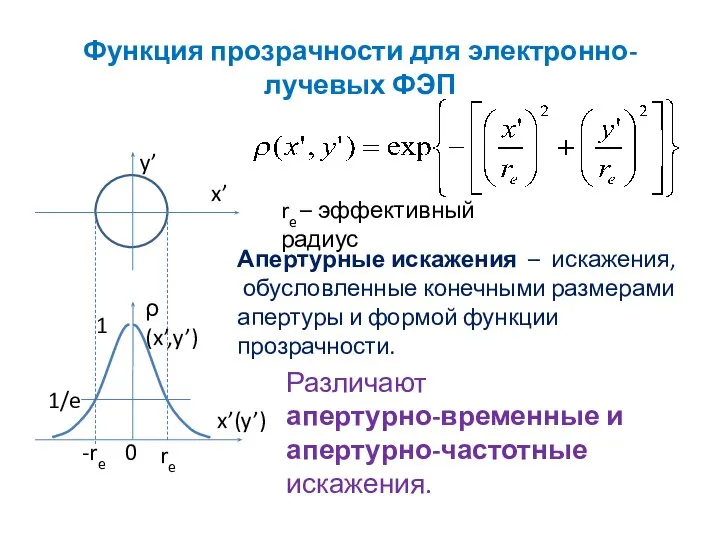
Функция прозрачности для электронно-лучевых ФЭП
re – эффективный радиус
Апертурные искажения – искажения,
обусловленные конечными размерами
апертуры и формой функции прозрачности.
Различают
апертурно-временные и
апертурно-частотные искажения.

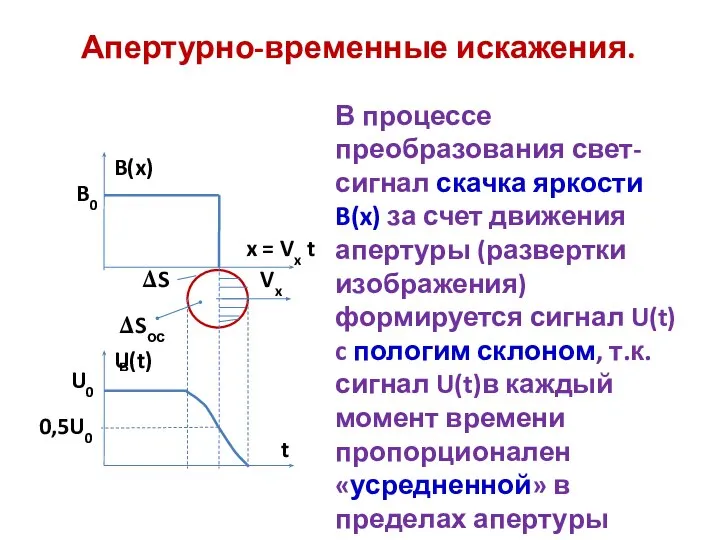
Апертурно-временные искажения.
0,5U0
В процессе преобразования свет-сигнал скачка яркости B(x) за счет движения апертуры (развертки изображения) формируется сигнал U(t) c пологим склоном, т.к. сигнал U(t)в каждый момент времени пропорционален «усредненной» в пределах апертуры яркости.
ΔSосв

Апертурно-временная (переходная) характеристика.
E(x,y) = dF/dS – освещенность мишени ФЭП
dF = EdS = EdS(x+x`,y+y`)dx`dy` – световой поток, падающий на dS апертуры.
dF` = ρ(x`,y`)dF –световой поток, прошедший через dS апертуры.
Составляющая фототока, вызванная световым потоком dF`: di = εdF`,
Тогда, ток ФЭП определяется выражением

Пусть E = E0 = const (освещенность постоянна).
Тогда ток на выходе ФЭП также постоянен:
При скачке освещенности в направлении x ток ФЭП определяется освещенной частью апертуры:
P0 – интегральная прозрачность
P(x) – интегральная прозрачность освещенной части апертуры.

Переходная характеристика:
H(x) = i(x)/i0 = P(x)/P0
Распределение прозрачности в сечении x’ = cons
Тогда
И учитывая симметрию апертуры получаем:

Для нормальной ТВ системы с квадратной апертурой: ρ(x`,y`) = 1 в пределах квадрата.
Тогда площадь сечения функции прозрачности R(x`) = d, а интегральная прозрачность P0 = d2 .
Учитывая, что
получаем
Так как x= vt, d = vτ, то

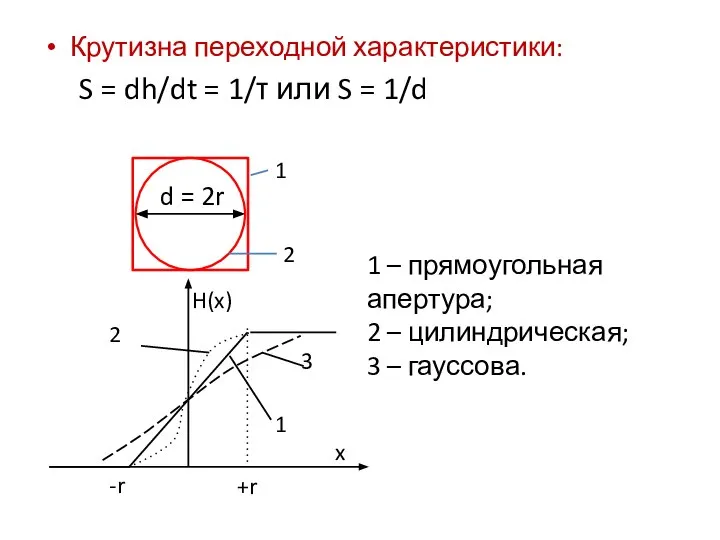
Крутизна переходной характеристики:
S = dh/dt = 1/τ или S = 1/d
1
2
1 – прямоугольная апертура;
2 – цилиндрическая;
3 – гауссова.
d = 2r

Апертурно-частотная характеристика ФЭП
B(x)
Bmax
Bmin
Vx

d – размер развертывающей апертуры;
Xi = 2di – переменный шаг штриховой миры;
νi = 1/Xi – пространственная частота миры;
Глубина модуляции видеосигнала
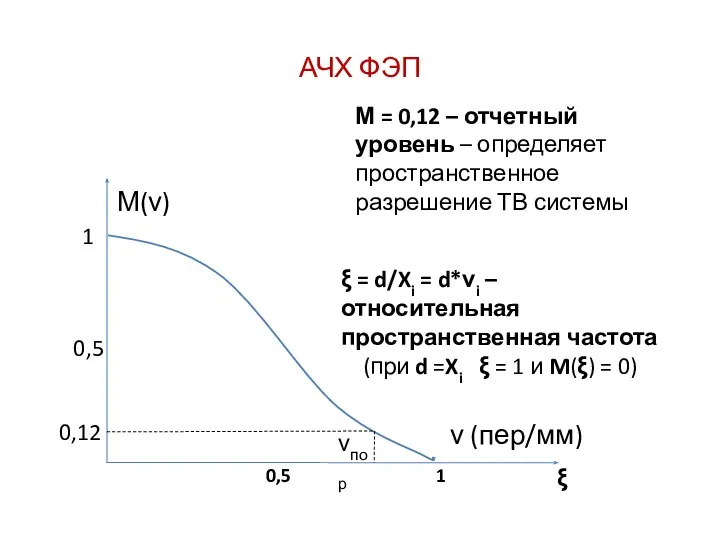
Если изображение представляет собой вертикальную штриховую миру с переменным шагом, то при увеличении пространственной частоты миры увеличивается частота сигнала и уменьшается глубина модуляции М (при Xi/2

АЧХ ФЭП
М = 0,12 – отчетный уровень – определяет пространственное разрешение ТВ системы
ξ = d/Xi = d*νi –относительная
пространственная частота
(при d =Xi ξ = 1 и M(ξ) = 0)
ξ
0,5
1

Пространственное разрешение ТВ системы в телевизионных линиях (ТВЛ)
ТВЛ – количество различаемых черных и белых штрихов штриховой миры, приходящихся на длину строки (вдоль X), равную высоте экрана:
Nб – количество белых полосок
Nч – количество черных полосок
N = Nб + Nч - ТВЛ
В ТВ системах 625 строк ТВЛ = 500…650

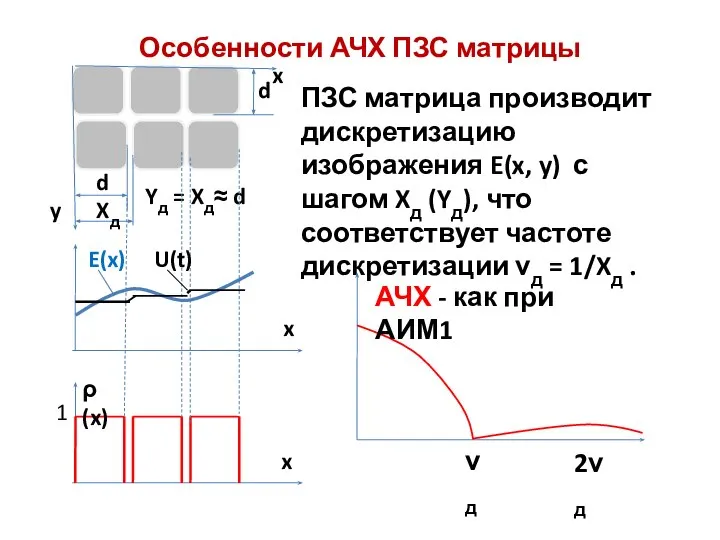
Особенности АЧХ ПЗС матрицы
ПЗС матрица производит дискретизацию изображения E(x, y) с шагом Xд (Yд), что соответствует частоте дискретизации νд = 1/Xд .
νд
2νд
АЧХ - как при АИМ1
1