Содержание
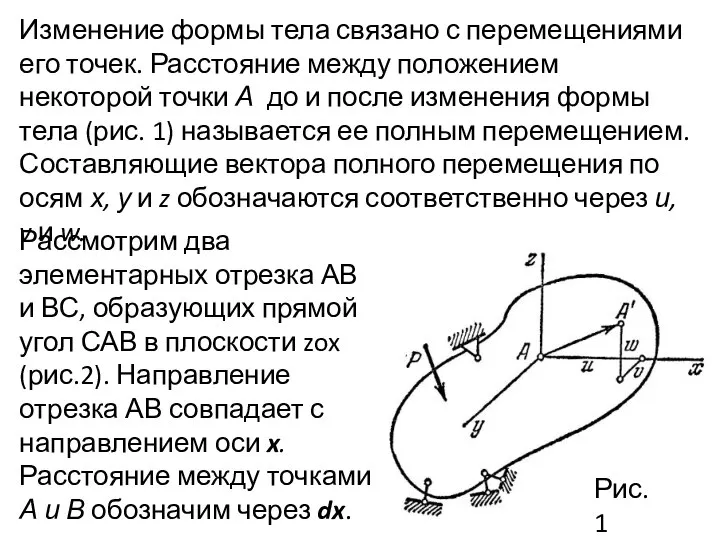
- 2. Изменение формы тела связано с перемещениями его точек. Расстояние между положением некоторой точки А до и
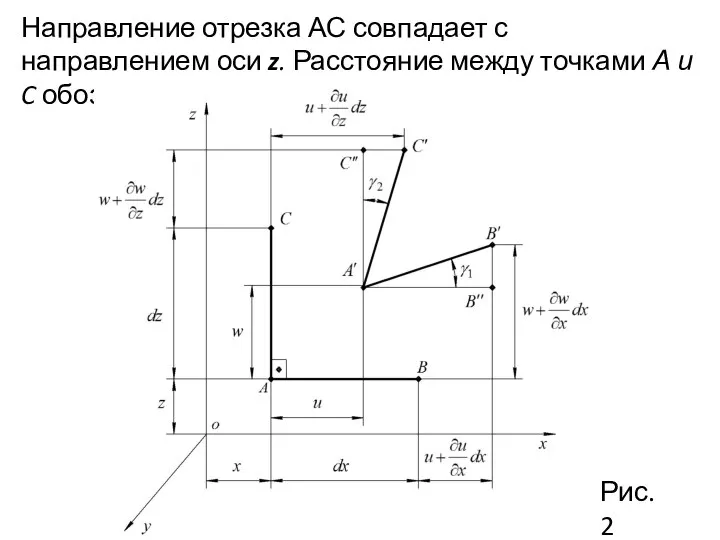
- 3. Направление отрезка АС совпадает с направлением оси z. Расстояние между точками А и C обозначим через
- 5. где - проекция отрезка на ось x. Из рисунка 2 очевидно Тогда
- 6. где - проекция отрезка на ось z. Тогда Рассуждая аналогично, можно получить
- 7. Угловая деформация (угол сдвига) в плоскости zox
- 8. В итоге, угловая деформация (угол сдвига) в плоскости zox
- 9. Аналогично могут быть написаны выражения для углов сдвига в двух других координатных плоскостях. В итоге имеем
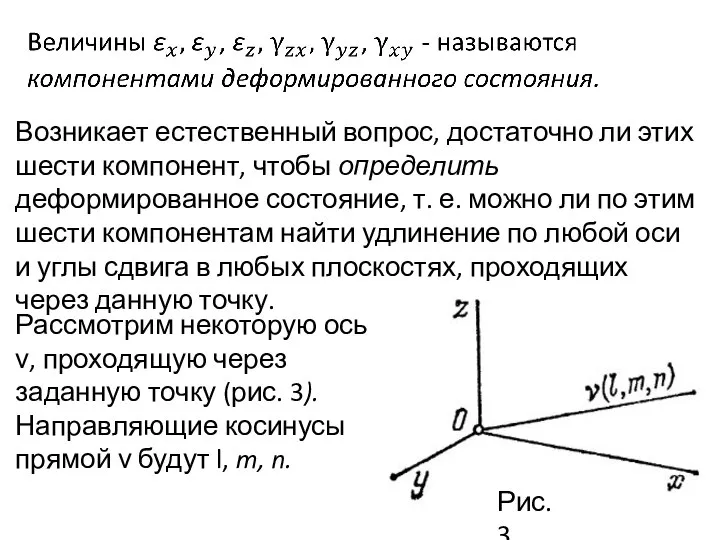
- 10. Возникает естественный вопрос, достаточно ли этих шести компонент, чтобы определить деформированное состояние, т. е. можно ли
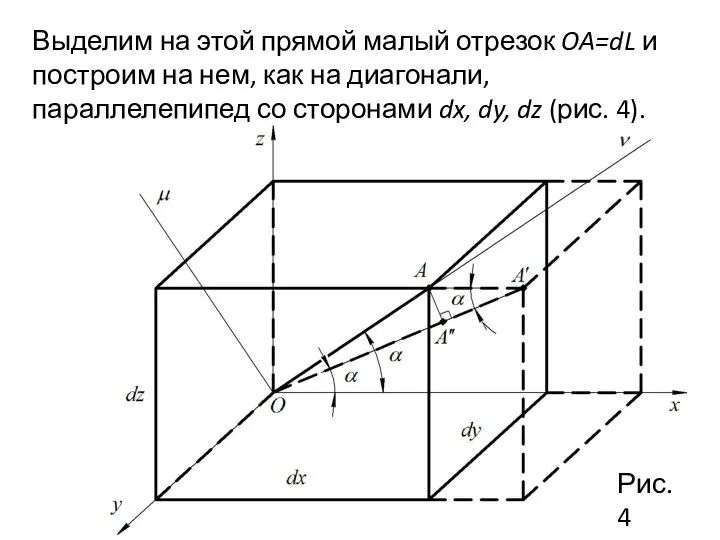
- 11. Выделим на этой прямой малый отрезок OA=dL и построим на нем, как на диагонали, параллелепипед со
- 12. (отрезок А′А′′ на рис.4) Относительное удлинение диагонали получим, разделив это произведение на dL=dx/l
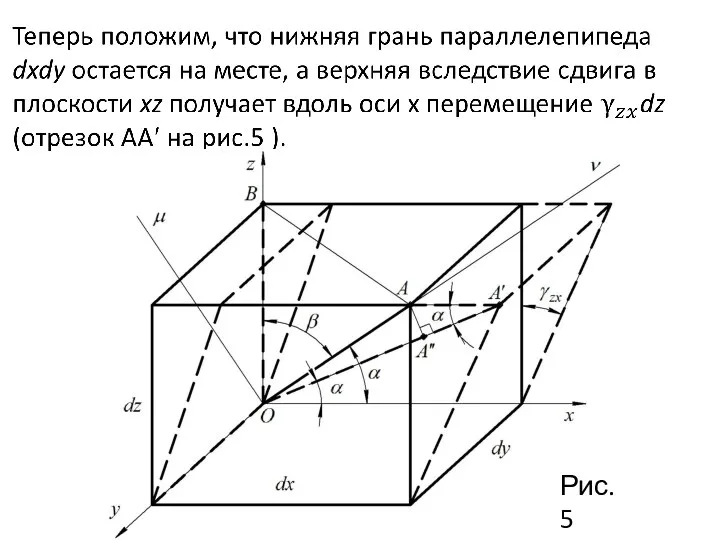
- 13. Рис.5
- 14. Диагональ OA получает абсолютное удлинение (отрезок А′А′′ на рис.5) Относительное удлинение диагонали получим, разделив это произведение
- 15. Несколько сложнее определить угол сдвига в плоскости, определяемой двумя взаимно перпендикулярными прямыми ν и μ (рис.
- 16. Таким образом, анализ деформированного состояния показывает, что оно обладает свойствами, совершенно аналогичными свойствам напряженного состояния.
- 17. Среди множества осей, которые могут быть проведены через исследуемую точку, существуют три взаимно перпендикулярные оси, в
- 18. Коэффициентами уравнения (3) являются инварианты деформированного состояния:
- 19. Подобно кругам Мора в напряжениях, можно построить круги Мора в деформациях. Анализ деформированного состояния основан на
- 20. Раскрывая скобки и пренебрегая произведениями линейных деформаций как величинами, малыми по сравнению с их первыми степенями,
- 21. Относительное изменение объема обозначается буквой е и равно сумме линейных деформаций по трем осям С поворотом
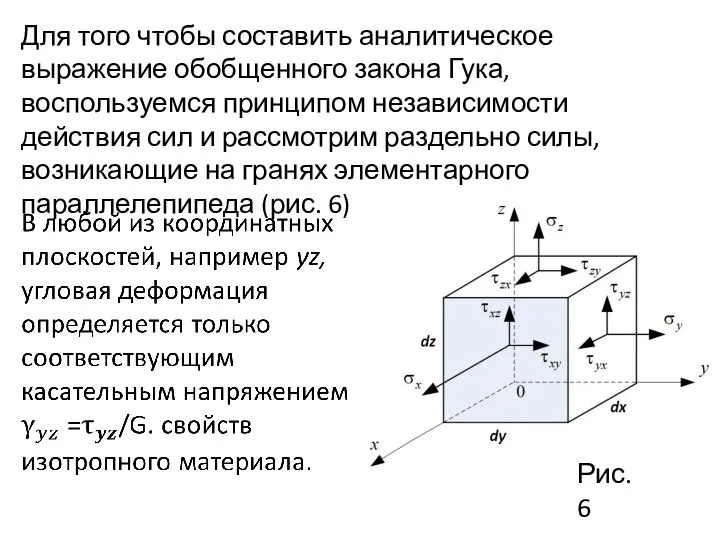
- 22. Обобщенный закон Гука Между компонентами напряженного состояния, с одной стороны, и деформированного — с другой, существует
- 23. Для того чтобы составить аналитическое выражение обобщенного закона Гука, воспользуемся принципом независимости действия сил и рассмотрим
- 24. Из этих выражений видно, что для изотропного тела главные оси напряженного и деформированного состояний совпадают, поскольку
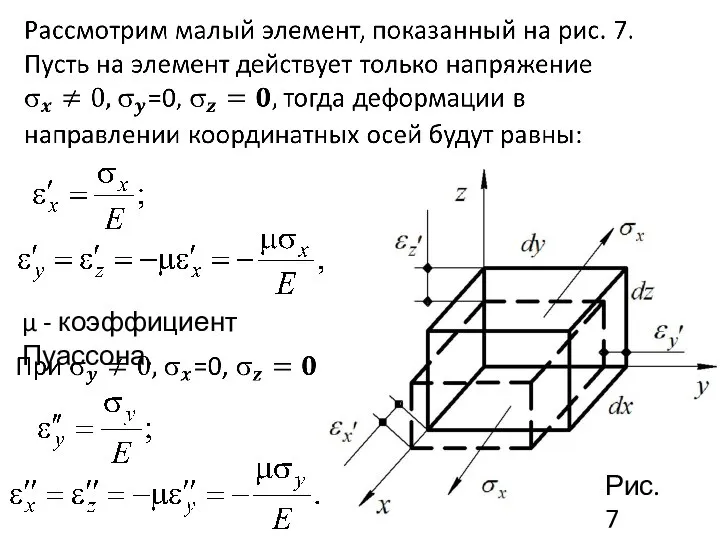
- 25. Подобно тому как угловые деформации не зависят от нормальных напряжений, линейные деформации не зависят от касательных
- 26. Рис.7 μ - коэффициент Пуассона.
- 27. Деформация удлинения в направлении оси x при совместном действии всех напряжений будет равна
- 28. Аналогичным образом определятся деформации в направлении других координатных осей. В итоге получим три уравнения связывающие осевые
- 29. Сложив левые и правые части выражений (5), получим выражение объемной деформации Уравнения (4), (5) и (6),
- 30. При положительном р величина е должна быть также положительной, при отрицательном р изменение объема будет отрицательным.
- 31. Потенциальная энергия деформации в общем случае напряженного состояния
- 32. Выражения остальных слагаемых внутренней энергии получаются простой перестановкой индексов. В итоге имеем Если энергию отнести к
- 33. Подставляя в последнее выражение формулы (4) и (5) получим: или в главных напряжениях
- 34. Для того чтобы найти потенциальную энергию во всем объеме деформированного тела, выражение (7) следует умножить на
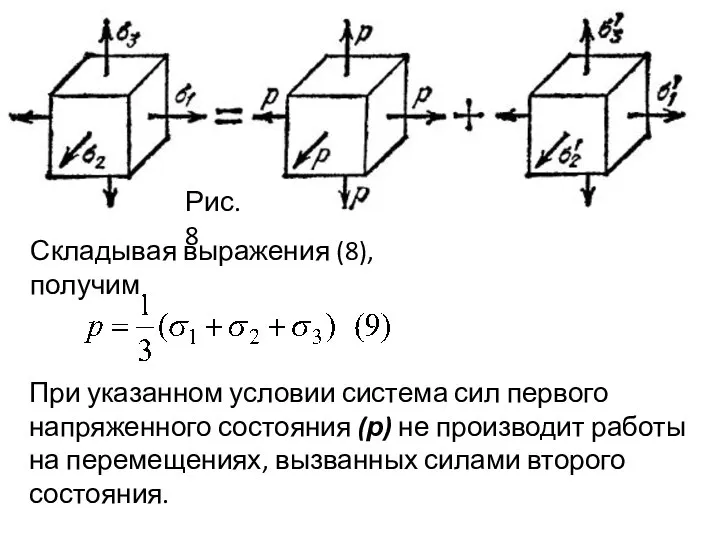
- 35. Каждое из главных напряжений представляем в виде суммы двух величин в результате чего напряженное состояние разбивается
- 36. Рис.8 Складывая выражения (8), получим При указанном условии система сил первого напряженного состояния (р) не производит
- 37. Точно так же и силы второго напряженного состояния не производят работы на перемещениях первого. Взаимные работы
- 39. Скачать презентацию




























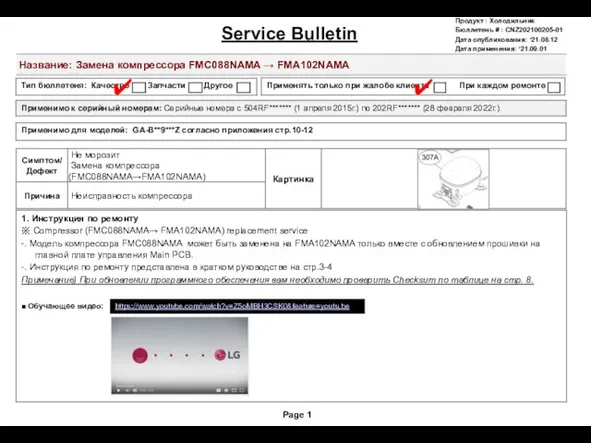 SVC Bulletin. Замена компрессора FMC088NAMA на FMA102NAMA
SVC Bulletin. Замена компрессора FMC088NAMA на FMA102NAMA Видатні вчені фізики. (8 клас)
Видатні вчені фізики. (8 клас) Электричество и магнетизм. Лекция № 3
Электричество и магнетизм. Лекция № 3 Плотность вещества
Плотность вещества Электро-диффузионные явления
Электро-диффузионные явления Солнечное излучение как совокупность ресурсов
Солнечное излучение как совокупность ресурсов Углы установки колес автомобиля
Углы установки колес автомобиля Альтернативные источники энергии
Альтернативные источники энергии 02_4_Hydraulics_Brakes and axle-rus
02_4_Hydraulics_Brakes and axle-rus Закон сохранения импульса
Закон сохранения импульса Радиоизотопное излучение
Радиоизотопное излучение Электрическая цепь. Электрическая схема
Электрическая цепь. Электрическая схема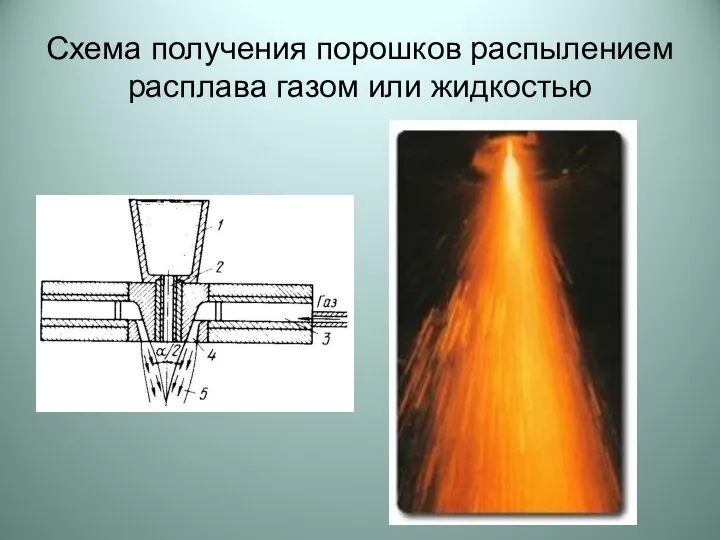 Схема получения порошков распылением расплава газом или жидкостью
Схема получения порошков распылением расплава газом или жидкостью Презентация на тему КПД тепловых двигателей (8 класс)
Презентация на тему КПД тепловых двигателей (8 класс)  Презентация на тему Постоянные магниты Магнитное поле Земли
Презентация на тему Постоянные магниты Магнитное поле Земли  Презентация на тему Энергия связи Дефект масс
Презентация на тему Энергия связи Дефект масс  Реактивное движение в технике, животном и растительном мире. 10 класс
Реактивное движение в технике, животном и растительном мире. 10 класс Lect__НСО
Lect__НСО Свойства жидкости
Свойства жидкости Аккумулирование энергии
Аккумулирование энергии Бронзы в машиностроении (творческая работа)
Бронзы в машиностроении (творческая работа) Загадочные явления в Воде, на Земле, в Космосе. 7 класс
Загадочные явления в Воде, на Земле, в Космосе. 7 класс Постоянный ток
Постоянный ток Физико-механические свойства
Физико-механические свойства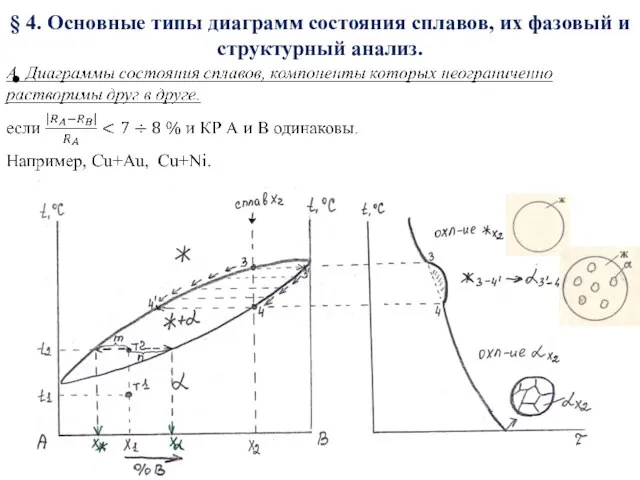 Диаграммы состояния сплавов, их фазовый и структурный анализ
Диаграммы состояния сплавов, их фазовый и структурный анализ Законы Ньютона
Законы Ньютона История развития тепловых машин
История развития тепловых машин Расчёт коэффициента торможения (Лекция 2)
Расчёт коэффициента торможения (Лекция 2)