Слайд 26.2. Динамика твёрдого тела.
6.2.1. Динамика поступательного движения.
Внешние и внутренние силы.
Для определения влияния

взаимодействия тел на характер движения т.т. разделим, прежде всего, все силы, действующие на т.т. на два вида. Внутренние силы – это силы, действующие между частицами самого т.т.; и внешние силы – это силы, действующие на частицы твёрдого тела со стороны тел, не принадлежащих т.т.
Слайд 3Второй закон Ньютона для т.т.

Слайд 4Общее уравнение движения т.т.

Слайд 6Закон изменения полного импульса т.т.

Слайд 8Полный импульс через радиус-вектор ц.м.

Слайд 9Полный импульс и скорость движения ц.м.т.т.

Слайд 116.2.2. Динамика вращательного движения.

Слайд 15Преобразование левой части равенства.

Слайд 17Замечание.
Момент импульса учитывает с одной стороны скорость вращения т.т., а с

другой его массу и её распределение относительно оси вращения.
Слайд 18Следствия из определения момента импульса.

Слайд 20Теорема о полном моменте импульса.

Слайд 22Формула двойного векторного произведения.

Слайд 25Момент инерции точки.
Определение. Моментом инерции м.т. Называется величина, численно равная произведению массы

материальной точки на квадрат расстояния до оси вращения.
Эта величина является аналогом понятия массы для поступательного движения. Она показывает насколько трудно раскрутить данную точку относительно оси вращения.
Слайд 28Закон изменения момента импульса т.т.

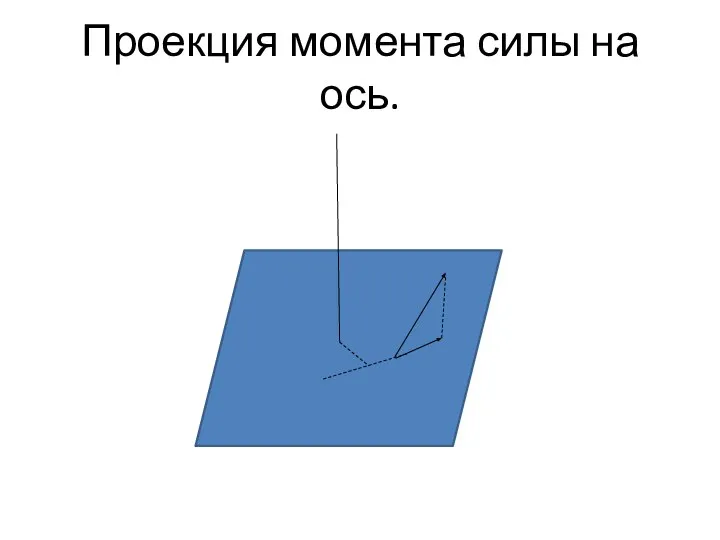
Слайд 29Плечо силы.
Для отыскания проекции момента некоторой силы на некоторую ось нужно спроецировать

силу на плоскость, перпендикулярную оси, и умножить величину этой проекции на расстояние от оси до линии-проекции силы на плоскость, перпендикулярную оси. Это расстояние называется плечом силы. Т.о. проекция момента силы на ось равна произведению проекции этой силы на плоскость, перпендикулярную оси, на её плечо.
Слайд 31Основное уравнение динамики вращательного движения т.т.

Слайд 33Формулировка основного уравнения динамики вращательного движения т.т.

Слайд 34Демонстрационный эксперимент.
Progr D: Progr E: Progr F: Progr G:

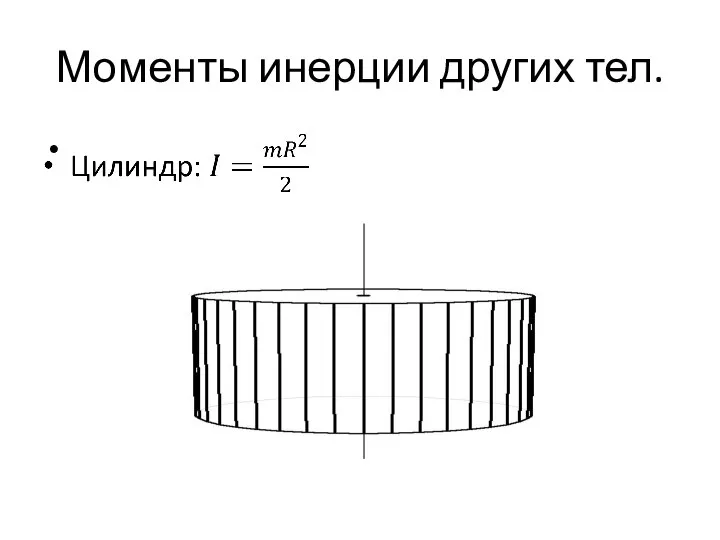
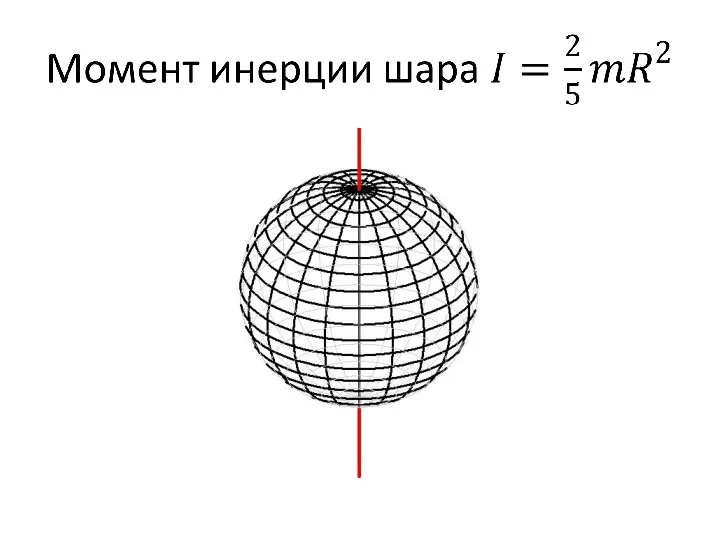
Слайд 356.2.3. Моменты инерции различных тел.

Слайд 36Расчёт момента инерции с помощью плотности т.т.

Слайд 37Момент инерции т.т. плоской формы.

Слайд 38Момент инерции т.т. линейной формы.










































 Фотоэффект. Законы фотоэффекта. Завершение классической физики
Фотоэффект. Законы фотоэффекта. Завершение классической физики Лабораторная работа №2 Измерение размеров малых тел
Лабораторная работа №2 Измерение размеров малых тел Презентация на тему Интерференция волн
Презентация на тему Интерференция волн  Тепловой расчет полупроводников
Тепловой расчет полупроводников Тест по физике в форме ЕГЭ, часть А
Тест по физике в форме ЕГЭ, часть А Цвет. Тест
Цвет. Тест Автобус, двигаясь прямолинейно и равноускоренно
Автобус, двигаясь прямолинейно и равноускоренно PRавый коронный, левый электронный. Рентген Попова или прибор захвативший весь мир
PRавый коронный, левый электронный. Рентген Попова или прибор захвативший весь мир Контрольная работа №5. Решения
Контрольная работа №5. Решения Звуковые колебания
Звуковые колебания Методы измерения скорости света
Методы измерения скорости света Прозрачный люминесцентный солнечный концентратор
Прозрачный люминесцентный солнечный концентратор Особенности водно-химического режима в контурах ЯЭУ
Особенности водно-химического режима в контурах ЯЭУ Специальные заклепки
Специальные заклепки Шумы транзисторов
Шумы транзисторов Сравнение основных параметров импульсных и линейных источников питания
Сравнение основных параметров импульсных и линейных источников питания Презентация на тему Второй закон термодинамики
Презентация на тему Второй закон термодинамики  Презентация на тему Электромагнитная природа света
Презентация на тему Электромагнитная природа света  Действие магнитного поля на проводник с током. Сила ампера. Сила лоренца
Действие магнитного поля на проводник с током. Сила ампера. Сила лоренца Общий осмотр автомобиля Toyota Mark II
Общий осмотр автомобиля Toyota Mark II Periodicheskoe
Periodicheskoe Рассеивающие линзы
Рассеивающие линзы Измерительные приборы для проведения измерения электрических величин
Измерительные приборы для проведения измерения электрических величин Простые механизмы. Момент силы. Золотое правило механики
Простые механизмы. Момент силы. Золотое правило механики Презентация без названия (1)
Презентация без названия (1) Презентация на тему Возможно ли создать электричество дома
Презентация на тему Возможно ли создать электричество дома  Термодинамика. ЕГЭ по физике
Термодинамика. ЕГЭ по физике Электромагнитные волны
Электромагнитные волны