Слайд 2Содержание
Физик, открывший эффект;
Эффект Холла;
Квантовый эффект Холла;
Особенность поведения двумерной электронной системы в магнитном

поле;
Суть квантового эффекта Холла;
Важность эффекта;
Список литературы
Слайд 3Э́двин Ге́рберт Холл — американский физик, открывший эффект, названный его именем (эффект Холла).
Эффект,

получивший впоследствии имя первооткрывателя, был открыт Эдвином Холлом в 1879 году, когда он работал над своей докторской диссертацией. Он обнаружил явление возникновения ЭДС в пластине полупроводника
Слайд 4Сила Лоренца
действующая на электроны со стороны холловского поля сила
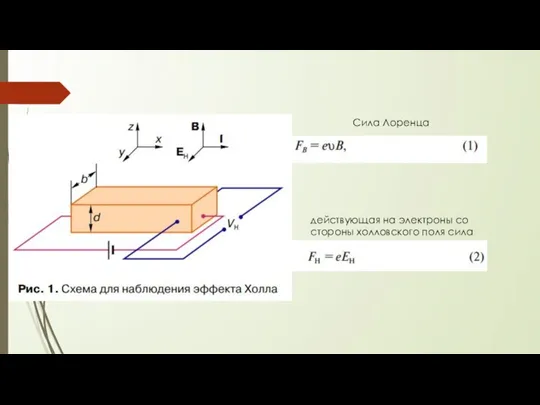
Слайд 8Особенность поведения двумерной электронной системы в магнитном поле

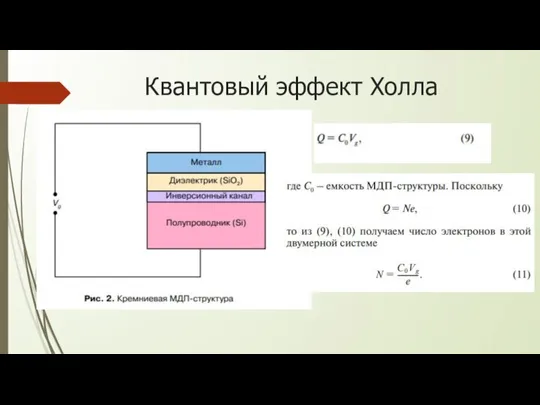
Слайд 10Суть квантового эффекта Холла
Движение электронов под действием внешнего электрического поля в проводниках

качественно можно представить себе следующим образом: благодаря внешнему электрическому полю, созданному источником ЭДС, электрон в проводнике движется с ускорением и плавно увеличивает свою энергию до тех пор, пока при столкновении с дефектом кристаллической решетки не потеряет приобретенную энергию, после чего процесс плавного ускорения электрона повторяется вновь. Такое скачкообразное движение электрона характеризуется средней скоростью упорядоченного движения (дрейфовой скоростью) υ, которая и определяет силу тока (5). Таким образом, протекание тока I вдоль оси x (рис. 1) неразрывно связано с возможностью плавного увеличения энергии электрона под действием внешнего электрического поля.
Слайд 11Пусть электрон движется по циклотронной орбите с центром в точке 1, изображенной

на рис. 4. При столкновении с рассеивающим центром S электрон перескочит на циклотронную орбиту с центром в точке 2. Таким образом, при наличии рассеяния электрон уже нельзя считать локализованным в пределах одной циклотронной орбиты: движение электрона в плоскости (x, y) становится делокализованным, что в соответствии с основными принципами квантовой механики приводит к исчезновению дискретного характера энергетического спектра.
Слайд 12Рассматривая изображенный на рис. 4 процесс рассеяния электрона из состояния с центром

циклотронной орбиты в точке 1 (состояние 1) в состояние с центром циклотронной орбиты в точке 2 (состояние 2), мы предполагали, что состояние 2 не занято другим электроном (в противном случае этот процесс рассеяния оказался бы невозможен из-за принципа Паули, запрещающего двум электронам находиться в одном состоянии). Предположение о том, что состояние 2 свободно и рассеяние электрона возможно, вполне справедливо для случая, когда число электронов на уровне Ландау незначительно по сравнению с числом электронов на полностью заполненном уровне Ландау N0 . В случае, когда число электронов на уровне Ландау оказывается равно N0 , все состояния на данном уровне оказываются заняты электронами и, несмотря на наличие рассеивающих центров, изображенный на рис. 4 переход электрона с одной циклотронной орбиты на другую в пределах одного уровня Ландау оказывается невозможен.
Слайд 14Важность эффекта
Изменяя Vg и измерив 1/Rн в тот момент, когда ток I

вдоль оси x обратится в нуль, можно с высокой точностью определить величину e²/h. Качественный вид экспериментальной зависимости величины 1/Rн от Vg , имеющей характерный вид лестницы, приведен на рис. 5. На ступеньках этой лестницы значения величины 1/Rн оказываются кратными e²/h. Замечательным оказывается то обстоятельство, что именно такая комбинация фундаментальных постоянных совместно со скоростью света с определяет фундаментальную мировую константу, называемую постоянной тонкой структуры и характеризующую взаимодействие электронов с электромагнитным излучением, которая в системе единиц СГСЭ имеет вид











 Ratownicze zestawy pneumatyczne
Ratownicze zestawy pneumatyczne Амплитуда колебаний в звуковой волне
Амплитуда колебаний в звуковой волне Альтернативные источники энергии
Альтернативные источники энергии Путь, перемещение, мгновенная скорость и ускорение
Путь, перемещение, мгновенная скорость и ускорение Лазеры. Принцип работы лазера. Лазерный луч
Лазеры. Принцип работы лазера. Лазерный луч Байр зүйн холбогч машины тухай
Байр зүйн холбогч машины тухай Нагревание проводников электрическим током. Закон Джоуля-Ленца
Нагревание проводников электрическим током. Закон Джоуля-Ленца LT-система физических единиц
LT-система физических единиц Разложение вектора по трём некомпланарным векторам
Разложение вектора по трём некомпланарным векторам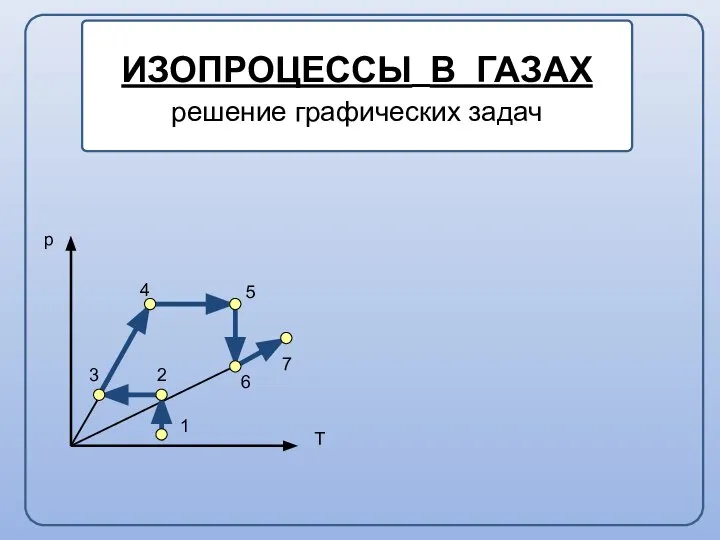 Изопроцессы в газах, решение графических задач
Изопроцессы в газах, решение графических задач Основные приёмы резания тонколистого металла и проволки
Основные приёмы резания тонколистого металла и проволки Характеристики телескопов. Задания
Характеристики телескопов. Задания Электрическое поле. Напряженность поля. 1 часть
Электрическое поле. Напряженность поля. 1 часть Молекулярная физика. Тепловые явления
Молекулярная физика. Тепловые явления Лабораторная работа. Изучение устройства и принципа работы термодымовой камеры КТД-100
Лабораторная работа. Изучение устройства и принципа работы термодымовой камеры КТД-100 Tvizi - Линейка электромобилей
Tvizi - Линейка электромобилей Напруження і деформації при згині
Напруження і деформації при згині Законы физики в стихах
Законы физики в стихах Закон Ома для участка цепи. Электрические явления. Законы постоянного тока
Закон Ома для участка цепи. Электрические явления. Законы постоянного тока Электромагнитная природа света. Скорость света
Электромагнитная природа света. Скорость света Дифракция света. Лекции 14-15
Дифракция света. Лекции 14-15 Рівновага складеної системи сил
Рівновага складеної системи сил Электромагниты. 8 класс
Электромагниты. 8 класс Задачи по физике. Вариант №1
Задачи по физике. Вариант №1 Двухтактный ДВС
Двухтактный ДВС Типичные затруднения при подготовке к ЕГЭ по физике
Типичные затруднения при подготовке к ЕГЭ по физике Решение задач по кинематики
Решение задач по кинематики Лекция 4 Классический метод расчета переходных процессов
Лекция 4 Классический метод расчета переходных процессов