Содержание
- 2. Основная литература Гуртов, В.А. Твердотельная электроника: учебное пособие для вузов / В. А. Гуртов. – 2-е
- 3. Тема I. Электронно-дырочный переход (p-n-переход). Свойства электронно-дырочного перехода. Вольт-амперная характеристика p-n-перехода. Диодная и диффузионная теория. Барьерная
- 4. 1. Свойства электронно-дырочного перехода. Полупроводниковая структура, содержащая две области с различными типами проводимости, носит название электронно-дырочного
- 5. Обозначим концентрации неосновных носителей заряда в n- и p- областях через p и n соответственно. Очевидно
- 6. Со временем между диффузионными потоками основных носителей зарядов и дрейфовыми потоками неосновных носителей зарядов устанавливается равновесие.
- 7. Приконтактная область обладает большим электрическим сопротивлением, так как, диффундируя во встречных направлениях через пограничный слой, дырки
- 8. Следовательно, (4) Известно, что в невырожденных полупроводниках при условии полной изоляции примесных атомов выражения для уровня
- 9. Из (11) следует, что величина потенциального барьера в области р- n- перехода, тем больше, чем сильнее
- 10. Для того, чтобы выяснить от чего зависит толщина слоя ОПЗ или p-n- перехода решают уравнение Пуассона
- 11. Из (18) и (19) при условии (21) получим, что (22) т.е. объемные заряды в области p-n-перехода
- 12. Формула (27) показывает, что чем выше степени легирования р- и n- областей полупроводниковой структуры с р-n-
- 13. 2. Вольт-амперная характеристика p-n-перехода. Если к р-n- переходу приложить внешнее напряжение U в прямом направлении, тогда
- 14. Для количественного описания ВАХ p-n- перехода рассматривают два случая: 1. Случай тонкого перехода, когда носители при
- 15. При рассмотрении ВАХ p-n - перехода по диодной теории делаются следующие предположения: 1. Контакты полупроводниковой структуры
- 16. (32) (33), где Dn и Dp – коэффициенты диффузии электронов и дырок соответственно. По пункту 4
- 17. Для нахождения распределения концентрации дырок в n- области и электронов в p- области решают стационарные уравнения
- 18. из (41) и (42) находим градиенты концентрации в слоях x = Ln, x = -Lp (43)
- 19. В случае толстого p-n – перехода (диффузионная теория) необходимо учитывать рекомбинацию в области p-n - перехода.
- 20. Полный ток через p-i-n- переход будет: (48) Вольт — амперная характеристика р-n -перехода. Теоретическая и экспериментальная.
- 21. Обратный ток в области насыщения IS для реального p-n - перехода больше теоретического и возрастает при
- 22. 3. Барьерная и диффузионная емкости. Как было отмечено выше р-n - переход в состоянии термодинамического равновесия
- 23. При наличии внешнего напряжения формулы для d и СБ принимают вид: (53) (54) где знак «
- 24. При обратном смещении инжекции нет, но диффузионная емкость проявляется при малых напряжениях за счет экстракции. Оценка
- 25. 2) случай W (56), где – среднее время диффузии носителей (дырок) через p- область, называемая временем
- 26. 4. Инжекция и экстракция неосновных носителей заряда. Если к p-n-переходу приложить внешнее напряжение, то через переход
- 27. Часть основных носителей, обладающие достаточной энергией, сравнимой с потенциальным барьером и больше могут преодолеть его и
- 28. 5. Распределение концентрации ННЗ у границ ЭДП при смещениях. Рассмотрим зависимость концентрации неосновных носителей заряда у
- 29. Концентрацию избыточных неосновных носителей заряда на границах обедненного слоя можно найти вычтя из концентрации на границе
- 30. Модель несимметричного диода: Wn > p. Уровнем инжекции называется отношение концентрации избыточных неосновных носителей заряда к
- 31. подставляя значение Δnp из (60) в (65) получим : np(x)=npo+npo exp(- ) (66) Аналогично для дырок
- 32. Аналогичное происходит и с дырками в n- области, поэтому концентрации их вблизи перехода определяется выражениями: np(0)=npo
- 33. 6. Пробой p-n - перехода. Под пробоем перехода понимают резкое возрастание тока при достижении обратным напряжением
- 34. Рассчитаем Uпроб резкого, близкого к симметричному, р-n – перехода. (72) С учетом того, что и формулу
- 35. Из (75) видно, что Uпроб обратно пропорционально концентрации примеси в первой степени. Туннельный пробой может происходить
- 36. Лавинный пробой происходит в достаточно толстых переходах при высоких обратных напряжениях, когда возникает ударная ионизация и
- 37. Обычно считается , а значит При наступает пробой. Для расчета связи М и α воспользуемся уравнением
- 38. Граничными условиями будут При x = 0 x = d (81) (82) или (82`) (83) или
- 39. Учитывая, что , можно подставить значение напряженности ε для резкого несимметричного n+-p – перехода, а затем
- 40. Соотношение между туннельным и лавинным пробоем может быть оценено с помощью следующего эмпирического правила. Если пробой
- 42. Скачать презентацию
Слайд 2Основная литература
Гуртов, В.А. Твердотельная электроника: учебное пособие для вузов / В. А.
Основная литература
Гуртов, В.А. Твердотельная электроника: учебное пособие для вузов / В. А.

Шалимова, К.В. Физика полупроводников: Учебник. 4-е изд., стер. — СПб.: Издательство «Лань», 2010. — 400 с.: ил.
Троян, П.Е. Твердотельная электроника. М.: ТУСУР, 2008. — 330 с.
Глазачев, А. В. Физические основы электроники. Конспект лекций /А. В. Глазачев, В. П. Петрович. – Томск, 2010. – 128 с. : ил.
Дополнительная литература
Лебедев А.И. Физика полупроводниковых приборов. М.: Физматлит, 2008. - 488 c.
О.В. Миловзоров, И.Г. Панков. Электроника. Учебник для вузов 4-е изд., стер. - М.: ВШ. 2008.
А.Л. Марченко. Основы электроники, уч. пос. для вузов. изд. ДМК Пресс. 2000.
Слайд 3Тема I. Электронно-дырочный переход (p-n-переход).
Свойства электронно-дырочного перехода.
Вольт-амперная характеристика p-n-перехода. Диодная и диффузионная
Свойства электронно-дырочного перехода.
Вольт-амперная характеристика p-n-перехода. Диодная и диффузионная

Барьерная и диффузионная емкости.
Инжекция и экстракция неосновных носителей заряда.
Распределение концентрации ННЗ у границ ЭДП при смещениях.
Пробой p-n-перехода (туннельный, лавинный и тепловой).
Слайд 41. Свойства электронно-дырочного перехода.
Полупроводниковая структура, содержащая две области с различными типами проводимости,
1. Свойства электронно-дырочного перехода.
Полупроводниковая структура, содержащая две области с различными типами проводимости,

Для создания р-n- перехода, обычно в полупроводниковый монокристалл вводят донорную и акцепторную примеси так, чтобы в одном кристалле образовались две граничащие области с различными типами проводимости. Физические свойства структуры с переходом определяются характером границы между этими областями.
На использовании свойства р-n- перехода основаны принципы работы большинства полупроводниковых приборов: диодов, транзисторов, фотодиодов, фотоэлементов, термоэлементов, светодиодов, инжекционных лазеров и т.д.
Процессы, происходящие в структуре с р-n–переходом при установлении равновесия.
Для того, чтобы рассмотреть процессы, происходящие в структуре с
р-n- переходом при установлении равновесия делают следующие предположения:
1) р-n- переход является резким, т.е. концентрация донорных атомов Nd в n- области постоянная до границы раздела, а на границе раздела меняется (уменьшается) скачкообразно. Аналогичным образом изменяется концентрация акцепторных примесных атомов Na в р- области.
2) Донорные и акцепторные атомы полностью ионизованны. Следовательно, концентрация основных носителей зарядов в р- и n- областях будет соответственно:
(1)
Слайд 5Обозначим концентрации неосновных носителей заряда в n- и p- областях через p
Обозначим концентрации неосновных носителей заряда в n- и p- областях через p

Очевидно nn>>pn, pn>>np и pp>>np, pn>>np.
3) В структуре n- и р- области полупроводника являются невырожденными и имеет место термодинамическое равновесие, а следовательно, для каждого из р- и п- полупроводников выполняется соотношение:
(2)
– собственная концентрация п/п.
4) р-n- переход несимметричный, т.е. Na > Nd (рис. 1)
Из вышеизложенного следует, что в области имеется резкий градиент концентрации электронов и дырок. В результате этого через р-n- переход наблюдаются диффузионные потоки электронов из n- области в р- область, а дырок в обратном направлении. При этом в приповерхностной области со стороны электронного полупроводника образуется положительный объемный заряд, а со стороны дырочного полупроводника - отрицательный объемный заряд (рис. 1 а,г). В области геометрической границы раздела между р- и n-областями образуется электрическое поле, направленное от n- области к р- области. Под действием электрического поля в приконтактной области начинается дрейф неосновных носителей заряда – электронов из дырочной области в n- область, а дырок из n- области в р- область.
Слайд 6Со временем между диффузионными потоками основных носителей зарядов и дрейфовыми потоками неосновных
Со временем между диффузионными потоками основных носителей зарядов и дрейфовыми потоками неосновных

При условии равновесия полный ток через р-n- переход равен 0, т.е.
(3)
Слайд 7 Приконтактная область обладает большим электрическим сопротивлением, так как, диффундируя во встречных направлениях
Приконтактная область обладает большим электрическим сопротивлением, так как, диффундируя во встречных направлениях

Полупроводниковые структуры с р-n- переходами бывают симметричные и несимметричные, резкие и плавные.
Р-n- переход симметричный, если концентрация донорных примесных атомов Nd в электронной области равна концентрации акцепторных атомов Na дырочной области.
P-n- переход является несимметричным, если Nd ≠ Na.
P-n- переход называется резким, если в области пространственного заряда (ОПЗ) концентрация приместных атомов изменяется скачком, если же в ОПЗ концентрации примесных атомов меняются плавно, то такой р- переход называется плавным. Для характеристики р-n- перехода применяются следующие параметры: потенциальный барьер (eφk), равновесная толщина слоя ОПЗ, емкость р-n- перехода.
Величину потенциального барьера eφk, возникающую в р-n- переходе в следствии различной концентрации носителей заряда в р- и n- областях, можно определить из следующих соображений: когда в структуре с р-n- переходом устанавливается термодинамическое равновесие уровни Ферми в р- и n- областях совпадают, а это приводит к изгибу энергетических зон в области р-n- перехода на величину равную разности уровней Ферми, когда р- и n- области изолированы. Эта разность в положении уровней Ферми в полупроводниках р- и n- типа и определяют величину потенциального барьера (рис.1 ж).
Слайд 8Следовательно,
(4)
Известно, что в невырожденных полупроводниках при условии полной изоляции примесных атомов
Следовательно,
(4)
Известно, что в невырожденных полупроводниках при условии полной изоляции примесных атомов

(5) – для полупроводника n-типа,
(6) – для полупроводника p-типа.
По статистике электронов в полупроводнике можно записать, что
(7)
(8)
Далее, согласно закону действующих масс, имеем
(9)
Из формул (4) – (9) можно получить следующие выражения для потенциального барьера:
(10)
(11)
Слайд 9Из (11) следует, что величина потенциального барьера в области р- n- перехода,
Из (11) следует, что величина потенциального барьера в области р- n- перехода,

(12)
Оценка величины потенциального барьера для полупроводниковой структуры с р-n- переходом из кристалла германия при таких данных Nd=10l6см-3, pn=1010см-3, Na=pp=1014 см-3, Т=300К, дает следующие значения для eφk =0.25эв.
Как сказано выше, в некоторой области р-n- перехода под действием контактного поля происходит обеднение основными носителями зарядов nn и рр и в этой области образуются объемные заряды: положительный объемный заряд со стороны полупроводника n- типа толщиной xn, отрицательный объемный заряд со стороны полупроводника р- типа толщиной xр. Общая толщина слоя пространственного заряда при условии равновесия будет:
(13)
Слайд 10Для того, чтобы выяснить от чего зависит толщина слоя ОПЗ или p-n-
Для того, чтобы выяснить от чего зависит толщина слоя ОПЗ или p-n-

(14) для области – xp ≤ x < 0
(15) для области – 0 < x ≤ xn
При следующих граничных условиях
при x = -xp (16)
при x = xn (17)
Решая уравнения (14) (15) при граничных условиях (16) и (17) получим распределение потенциала в ОПЗ в виде:
(18) для области -xp ≤ x < 0
(19) для области 0 < x ≤ xn
В областях p-n-перехода функции φ и dφ/dx являются непрерывными, т.е.
(21)
(20)
Слайд 11Из (18) и (19) при условии (21) получим, что
(22)
т.е. объемные заряды в
Из (18) и (19) при условии (21) получим, что
(22)
т.е. объемные заряды в

Из граничного условия (20) и формул (18) и (19) получим
Отсюда
(23)
(24)
Из (22) с учетом (13) получим
или
(25)
Подставляя значения xn, xp из (25) в (24) получим что
Отсюда
(26)
(27)
Слайд 12Формула (27) показывает, что чем выше степени легирования р- и n- областей
Формула (27) показывает, что чем выше степени легирования р- и n- областей

(28)
Важным параметром р-n- перехода является барьерная емкость. P-n- переход можно рассматривать как систему двух проводников, разделенных слоем очень малой концентрации свободных носителей заряда, т.е. слоем диэлектрика. Двойной электрический слой в области р-n- перехода представляет собой плоский конденсатор. Если толщина слоя объемного заряда d, площадь перехода S, то емкость такого конденсатора определяется выражением
(29)
Подставляя в (29) значения d из (28) получим
Емкость СБ называют барьерной емкостью p-n-перехода.
(30)
В общем случае
(31)
Слайд 132. Вольт-амперная характеристика p-n-перехода.
Если к р-n- переходу приложить внешнее напряжение U в
2. Вольт-амперная характеристика p-n-перехода.
Если к р-n- переходу приложить внешнее напряжение U в

Если к p-n- переходу подано смещение в обратном направлении, то потенциальный барьер увеличивается на величину eU для основных носителей заряда. При этом равновесие нарушается и уровень Ферми смещается на величину eU вверх.
При обратном смещении ток через p-n- переход осуществляется только потоком неосновных носителей зарядов.
Слайд 14Для количественного описания ВАХ p-n- перехода рассматривают два
случая:
1. Случай тонкого перехода, когда
Для количественного описания ВАХ p-n- перехода рассматривают два
случая:
1. Случай тонкого перехода, когда
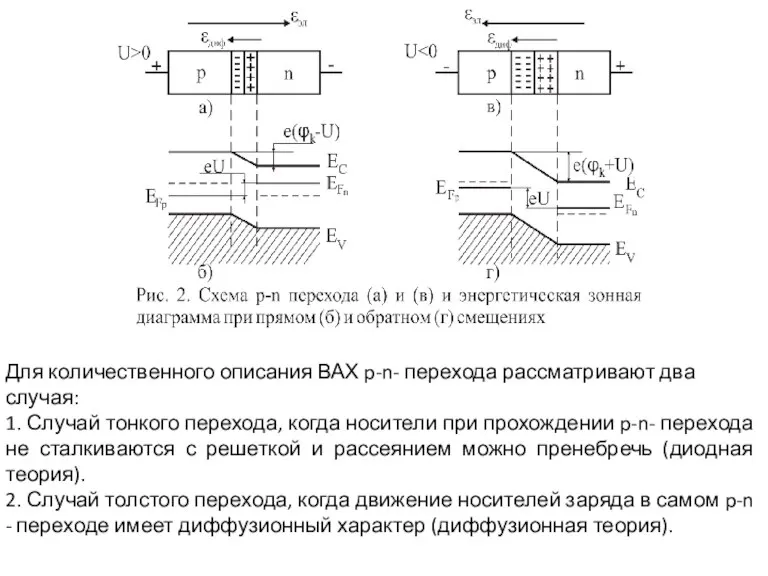
2. Случай толстого перехода, когда движение носителей заряда в самом p-n - переходе имеет диффузионный характер (диффузионная теория).
Слайд 15При рассмотрении ВАХ p-n - перехода по диодной теории делаются следующие предположения:
1.
При рассмотрении ВАХ p-n - перехода по диодной теории делаются следующие предположения:
1.

2. Все приложенное напряжение падает на область p-n - перехода, т.е. p- и n- области сильно легированы, поэтому падением напряжения на этих областях можно пренебречь;
3. P-n - переход работает в области малых напряжений, т.е. рассматривается слабый уровень инжекции pn << nn и np << pp;
4. Генерация и рекомбинация внутри области объемного заряда отсутствуют;
5. Рассматривается одномерная и стационарная задача;
6. Полупроводник предполагается невырожденным.
Согласно предположению (2) в структуре с p-n - переходом
процессы происходят таким образом, что за областью перехода электроны и дырки движутся только вследствие градиента концентрации, т.е. путем диффузии.
Слайд 16(32)
(33),
где Dn и Dp – коэффициенты диффузии электронов и дырок соответственно.
По пункту
(32)
(33),
где Dn и Dp – коэффициенты диффузии электронов и дырок соответственно.
По пункту

(34)
(35)
(36 )
Следовательно полный ток будет
Как видно из (36), для нахождения тока через диод нужно вычислить концентрацию носителей и их градиенты на границе перехода.
Слайд 17Для нахождения распределения концентрации дырок в n- области и электронов в p-
Для нахождения распределения концентрации дырок в n- области и электронов в p-

(37)
(38)
Решая уравнения (37) и (38) при граничных условиях вида
при x = 0 (39)
p = pn при x → ∞ (40)
получим распределение избыточной концентрации электронов и дырок в p- и n- областях соответственно.
(41)
(42)
Слайд 18из (41) и (42) находим градиенты концентрации в слоях x = Ln,
из (41) и (42) находим градиенты концентрации в слоях x = Ln,

(43)
(44)
используя (12), (13) и (5) получим ток через p-n- переход в виде:
(45)
величину
(46) называют током насыщения или тепловым током.
Из формул (45) и (46) можно сделать следующие выводы:
1. При прямом смещении на p-n - переходе (U >0) сила тока увеличивается по экспоненциальному закону;
2. При обратном смещении на p-n - переходе (U <0) сила тока стремится к постоянной величине Is;
3. Обратный ток (Is) определяется параметрами неосновных носителей заряда;
4. Обратный ток образуется дырками (электронами) генерируемыми, в единице объема полупроводника за 1с в слое шириной xn (хр) у p-n -перехода.
Слайд 19В случае толстого p-n – перехода (диффузионная теория) необходимо учитывать рекомбинацию в
В случае толстого p-n – перехода (диффузионная теория) необходимо учитывать рекомбинацию в

(47),
где xi – толщина слоя.
Слайд 20Полный ток через p-i-n- переход будет:
(48)
Вольт — амперная характеристика р-n -перехода. Теоретическая
Полный ток через p-i-n- переход будет:
(48)
Вольт — амперная характеристика р-n -перехода. Теоретическая

Как видно из рис.3 г ВАХ реального p-n - перехода несколько отличается от характеристики идеального р-n - перехода. Отличие прямой ветви ВАХ реального р-n - перехода обусловлено тем, что при выводе уравнения (45) не учитывались явления генерации и рекомбинации в запирающем слое, а так же сопротивления RБ объема полупроводника в области базы p-n- перехода. При увеличении прямого смещения ток вначале растет по экспоненциальному закон, а затем увеличение тока происходит по линейному закону. Это объясняется тем, что при больших прямых токах внешнее напряжение значительно превышает контактную разность потенциалов φk и прямой ток определяется, в основном, сопротивлением базы p-n - перехода.
Слайд 21Обратный ток в области насыщения IS для реального p-n - перехода больше
Обратный ток в области насыщения IS для реального p-n - перехода больше

(49)
где в – коэффициент зависящий от строения p-n- перехода.
IRБ – падение напряжения на базе диода.
Слайд 223. Барьерная и диффузионная емкости.
Как было отмечено выше р-n - переход в
3. Барьерная и диффузионная емкости.
Как было отмечено выше р-n - переход в

(50)
где d – толщина p-n- перехода в равновесном состоянии, ее величина определяется выражением вида:
(51)
Следовательно, барьерная емкость р-n - перехода в условиях термодинамического равновесия и при U = 0 имеет вид:
(52)
величина d, а следовательно, и барьерная емкость CБ зависит от величины и направления внешнего поля. Если на p-n - переход подано обратное смещение, то это приводит к увеличению высоты потенциального барьера, экстракции неосновных носителей заряда в области полупроводников прилегающей к р-n -переходу и к расширению барьерной емкости.
Слайд 23При наличии внешнего напряжения формулы для d и СБ принимают вид:
(53)
(54)
где знак
При наличии внешнего напряжения формулы для d и СБ принимают вид:
(53)
(54)
где знак

Если к р-n - переходу приложено внешнее напряжение в прямом направлении, то происходит инжекция неосновных носителей заряда в р- и n-области. При этом изменение внешнего напряжения приводит к изменению концентрации инжектированных носителей. Для нейтрализации инжектированных носителей заряда в области базы из внешней цепи подходят заряды противоположных знаков. Эти процессы являются диффузионными и воспринимаются внешней цепью как изменение емкости. Эту емкость называют диффузионной емкостью - СД .
Слайд 24При обратном смещении инжекции нет, но диффузионная емкость проявляется при малых напряжениях
При обратном смещении инжекции нет, но диффузионная емкость проявляется при малых напряжениях

Оценка величины диффузионной емкости для р-n -перехода с различной толщиной базы W приводит к следующим формулам:
1) случай W >> Lp, Ln, в этом случае все инжектированные носители заряда рекомбинируют в области базы, не достигая электрода. Для данного случая получена формула
(55)
Диффузионная емкость зависит от времени жизни инжектированных неосновных носителей заряда в базе р-n - перехода и величины прямого тока.
Слайд 252) случай W << Lp, Ln, в этом случае не все инжектированные
2) случай W << Lp, Ln, в этом случае не все инжектированные

(56),
где – среднее время диффузии носителей (дырок) через p- область, называемая временем пролета, δк – скорость рекомбинации носителей на электроде. В этом случае емкость зависит от I, W, Dp и δк.
Основные результаты, изложенные выше, и полученные формулы используются при выполнении следующих лабораторных работ по физике полупроводниковых и диэлектрических приборов:
Исследование фотодиода и фотоэлемента.
Исследование туннельных диодов.
Исследование выпрямительных диодов.
Исследование стабилитрона.
Исследование биполярного транзистора.
Слайд 264. Инжекция и экстракция неосновных носителей заряда.
Если к p-n-переходу приложить внешнее напряжение,
4. Инжекция и экстракция неосновных носителей заряда.
Если к p-n-переходу приложить внешнее напряжение,
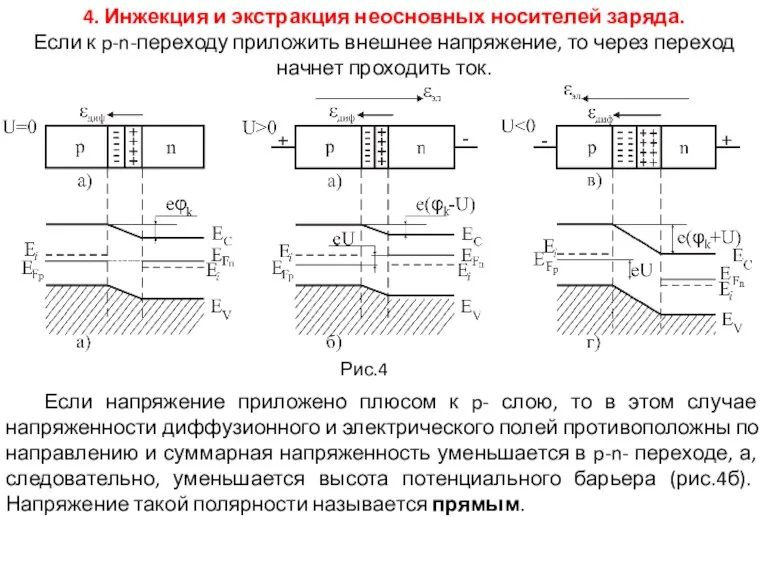
Рис.4.
Если напряжение приложено плюсом к p- слою, то в этом случае напряженности диффузионного и электрического полей противоположны по направлению и суммарная напряженность уменьшается в p-n- переходе, а, следовательно, уменьшается высота потенциального барьера (рис.4б). Напряжение такой полярности называется прямым.
Слайд 27Часть основных носителей, обладающие достаточной энергией, сравнимой с потенциальным барьером и больше
Часть основных носителей, обладающие достаточной энергией, сравнимой с потенциальным барьером и больше

Преодолевшие потенциальный барьер основные носители заряда оказываются в соседней области неосновными. При этом в близи перехода концентрация неосновных носителей – электронов в p – области, и дырок в n – области становится больше равновесной (рис. 5а) они диффундируют в глубь перехода и рекомбинируют там.
Повышение концентрации неосновных носителей заряда в p- и n- областях при прямых напряжениях называется инжекцией.
Область в которой происходит инжекция называется базой п/п прибора.
Если полярность на p-n- переходе изменить, то напряженность электрического поля и диффузионного совпадут и потенциальный барьер увеличится (рис. 4в) для основных носителей. Для неосновных носителей заряда, т.е для дырок в n- области и для электронов в p- области, потенциальный барьер в p-n- переходе вообще отсутствует. Неосновные носители будут втягиваться электрическим полем в p-n- переход и проходить в соседнюю область.
Уменьшение концентрации неосновных носителей при обратных напряжениях называется экстракцией. Ток при этом незначительный из-за малой концентрации неосновных носителей в прилегающих к p-n- переходу областях.
Такое включение напряжения называется обратным.
Слайд 285. Распределение концентрации ННЗ у границ ЭДП при смещениях.
Рассмотрим зависимость концентрации неосновных
5. Распределение концентрации ННЗ у границ ЭДП при смещениях.
Рассмотрим зависимость концентрации неосновных

(57)
Если вместо равновесной высоты потенциального барьера eφk в (57) подставить высоту потенциального барьера eφk – eU можно получить концентрацию неравновесных носителей заряда на границе обедненных слоев np(0) pn(0) (рис.5в)
np(0) = npoexp( )
(58)
pn(0) = pnoexp( )
(59)
Слайд 29Концентрацию избыточных неосновных носителей заряда на границах обедненного слоя можно найти вычтя
Концентрацию избыточных неосновных носителей заряда на границах обедненного слоя можно найти вычтя

(60)
(61)
С учетом того, что pno =ni2/ nno , npo = ni2/ ppo , Nd ≈ nno ; Na ≈ ppo поделив (60) на (61) получим
Т.к. nno>>ppo n+ - область будет больше инжектировать чем p – область, т.е. Δnp>Δpn.
В диодах несимметричной конструкции инжекция носит односторонний характер и главную роль играют носители инжектируемые из сильнолегированной (низкоомной) области в слаболегированную (высокоомную) область.
(62)
Слайд 30Модель несимметричного диода: Wn> p.
Уровнем инжекции называется отношение
Модель несимметричного диода: Wn Уровнем инжекции называется отношение
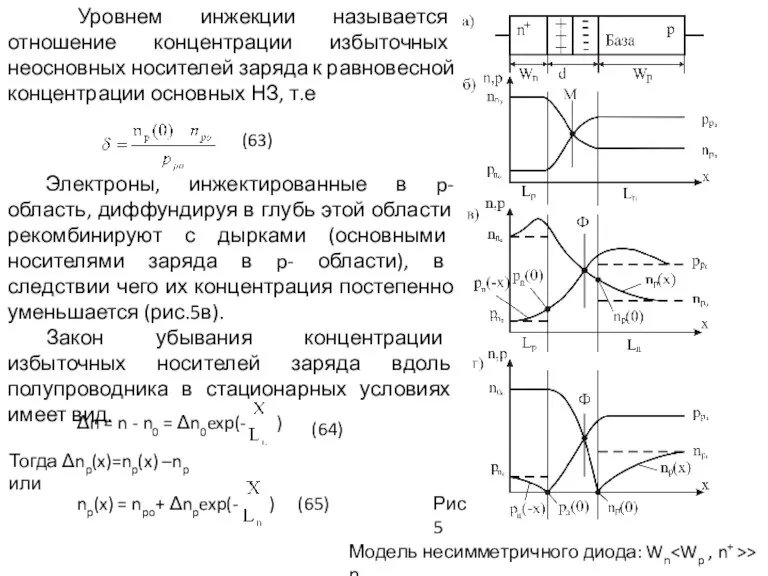
Электроны, инжектированные в p- область, диффундируя в глубь этой области рекомбинируют с дырками (основными носителями заряда в p- области), в следствии чего их концентрация постепенно уменьшается (рис.5в).
Закон убывания концентрации избыточных носителей заряда вдоль полупроводника в стационарных условиях имеет вид.
Δn = n - n0 = Δn0exp(- )
Тогда Δnp(x)=np(x) –np или
np(x) = npo+ Δnpexp(- )
(65)
(63)
(64)
Рис 5
Слайд 31подставляя значение Δnp из (60) в (65) получим :
np(x)=npo+npo exp(- )
(66)
Аналогично для
подставляя значение Δnp из (60) в (65) получим :
np(x)=npo+npo exp(- )
(66)
Аналогично для

pn(-x)=pno+pno exp(- )
(67)
Графики функций np(x) и pn(-x) при инжекции приведены на рисунке 5в.
Инжектированные носители создают вблизи перехода избыточные заряды, которые компенсируются приходящими из p- и n- областей основными носителями. Поэтому на расстояниях Ln и Lp концентрации основных носителей заряда pp(x) и nn(x) превышают равновесные (рис.5в).
С приложением к диоду обратного смещения n- и p- области вблизи перехода обедняются неосновными носителями заряда (рис.5г). Это объясняется тем, что электроны в p- области находящиеся на расстоянии диффузионной длины Ln могут попадать в поле перехода (тепловое движение) и перебрасываться в n- область. В результате концентрация неосновных носителей заряда в p- области вблизи перехода снижается.
Слайд 32Аналогичное происходит и с дырками в n- области, поэтому концентрации их вблизи
Аналогичное происходит и с дырками в n- области, поэтому концентрации их вблизи

np(0)=npo exp(-eU/kT) (68)
pn(0)=pno exp(-eU/kT) (69)
В направление от границ обедненного слоя концентрация неосновных носителей заряда возрастает, приближаясь к равновесной. Поэтому аналогично (66) и (67) получим аналитическое выражение для распределения неосновных носителей заряда при экстракции
np(x)=npo+npo [exp(-eU/kT-1]exp(-X/Ln) (70)
pn(-x)= pno+pno[exp(-eU/kT)-1]exp(X/Ln) (71)
Слайд 336. Пробой p-n - перехода.
Под пробоем перехода понимают резкое возрастание тока при
6. Пробой p-n - перехода.
Под пробоем перехода понимают резкое возрастание тока при

Туннельным пробоем p-n–перехода называют электрический пробой, вызванный квантово - механическим туннелированием носителей заряда сквозь тонкий потенциальный барьер без изменения энергии. Туннелирование электронов возможно при условии, если толщина потенциального барьера δ мала, которая определяется напряженностью электрического поля, т.е. наклоном энергетических уровней и зон. Следовательно, условия для туннелирования возникают только при определенной напряженности электрического поля или при определенном напряжении на p-n - переходе – при пробивном напряжении. Если величина обратного напряжения на переходе велика и выполняется условие , то границы зон перекрываются и при некоторой определенной напряженности электрического поля возможно туннелирование,
Рис. 6
Слайд 34Рассчитаем Uпроб резкого, близкого к симметричному, р-n – перехода.
(72)
С учетом того, что
Рассчитаем Uпроб резкого, близкого к симметричному, р-n – перехода.
(72)
С учетом того, что

(73)
Подставляя значение для резкого p-n – перехода при обратном смещении в (73), получим:
(74)
При напряжение на переходе будет пробивным, т.е.
или
(75)
т.е. электроны из валентной зоны полупроводника p- типа при неизменной энергии могут переходить в зону проводимости полупроводника n- типа. Это возможно при определенном напряжении на р-n - переходе, которое называется пробивным.
Слайд 35Из (75) видно, что Uпроб обратно пропорционально концентрации примеси в первой степени.
Туннельный
Из (75) видно, что Uпроб обратно пропорционально концентрации примеси в первой степени.
Туннельный

Если все-таки принять, что , с учетом того что (75) можно представить в виде:
С повышением температуры у большинства полупроводников ширина запрещенной зоны уменьшается, поэтому пробивное напряжение при туннельном пробое уменьшается с увеличением температуры.
(76)
Рис 7
Слайд 36Лавинный пробой происходит в достаточно толстых переходах при высоких обратных напряжениях, когда
Лавинный пробой происходит в достаточно толстых переходах при высоких обратных напряжениях, когда

Процесс лавинного умножения происходит не по всей площади перехода одновременно, а в отдельных областях локализации электрического поля - на дефектах кристаллической решетки и других неоднородностях. В областях локализации поля образуются микроплазмы, в которых идет процесс ЛУ. Микроплазмы нестабильны, что приводит к флуктуациям тока и появлению шумов лавинного пробоя.
Чтобы охарактеризовать увеличение тока из-за процесса ударной ионизации в выпрямляющем переходе, вводят коэффициенты лавинного умножения Мn и Мр , которые показывают отношение тока данных носителей заряда, выходящих из перехода, к току тех же носителей, входящих в переход.
Слайд 37Обычно считается , а значит
При наступает пробой.
Для расчета связи М и
Обычно считается , а значит
При наступает пробой.
Для расчета связи М и

(77)
При установившемся процессе , можно пренебречь рекомбинацией в p-n – переходе при большом обратном напряжении, т.е. Rn = 0. Тогда
(78)
Если выделить единичный объем, то каждый проходящий через этот объем носитель образует в нем количество носителей равное коэффициенту ионизации α, а в единицу времени через рассматриваемый объем проходит j /е носителей. Тогда с учетом генерации в результате ионизации атомов электронами и дырками получим:
(79)
Подставляя (79) в (78) имеем:
(80)
Слайд 38 Граничными условиями будут
При x = 0
x = d
Граничными условиями будут
При x = 0
x = d

(81)
(82) или
(82`)
(83) или
(84)
Так, как при наступает пробой, то условием лавинного пробоя будет
(86)
(85) связь между коэффициентом лавинного размножения с коэффициентом ударной ионизации.
Слайд 39Учитывая, что , можно подставить значение напряженности ε для резкого несимметричного n+-p
Учитывая, что , можно подставить значение напряженности ε для резкого несимметричного n+-p

(86), где b изменяется от 3 до 6 и зависит от профиля легирования.
Пробивное напряжение можно представить в виде
(87)
B и а – эмпирические коэффициенты различные, даже для диодов из одного и того же материала с разными резкими p-n – переходами. Это связано с различными подвижностями.
Si: p+- n – Uпр = 96ρ0,78; n+- p – Uпроб = 49ρ0,78
Ge: p+- n – Uпр = 100ρ0,8; n+- p – Uпроб = 55ρ0,8
С повышением температуры уменьшается длина свободного пробега носителей заряда, а значит и энергия, которую может приобрести носитель, на этой длине и её уже недостаточно для ионизации атома полупроводника. Следовательно повышение температуры приводит к увеличению пробивного напряжения при лавинном пробое.
Слайд 40Соотношение между туннельным и лавинным пробоем может быть оценено с помощью следующего
Соотношение между туннельным и лавинным пробоем может быть оценено с помощью следующего
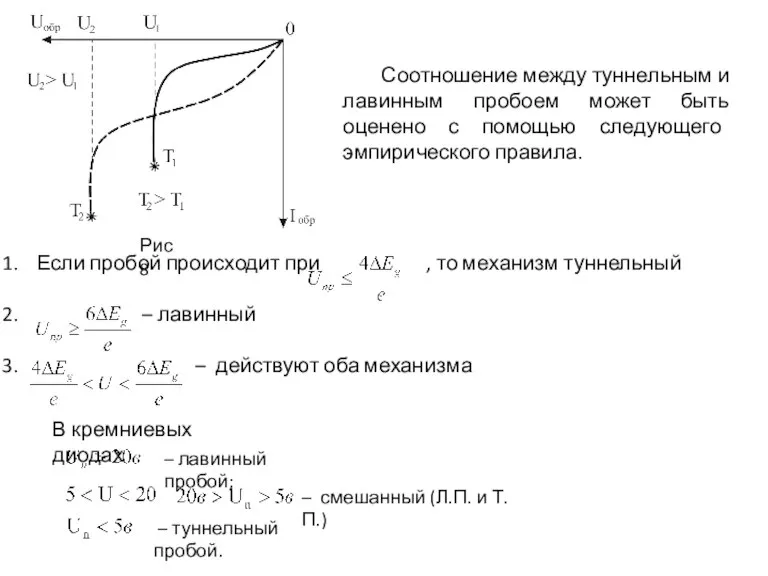
Если пробой происходит при , то механизм туннельный
– лавинный
– действуют оба механизма
В кремниевых диодах
– лавинный пробой;
– смешанный (Л.П. и Т.П.)
– туннельный пробой.
Рис 8
 Апертурные искажения. Форма и функция прозрачности развертывающего элемента
Апертурные искажения. Форма и функция прозрачности развертывающего элемента Механика
Механика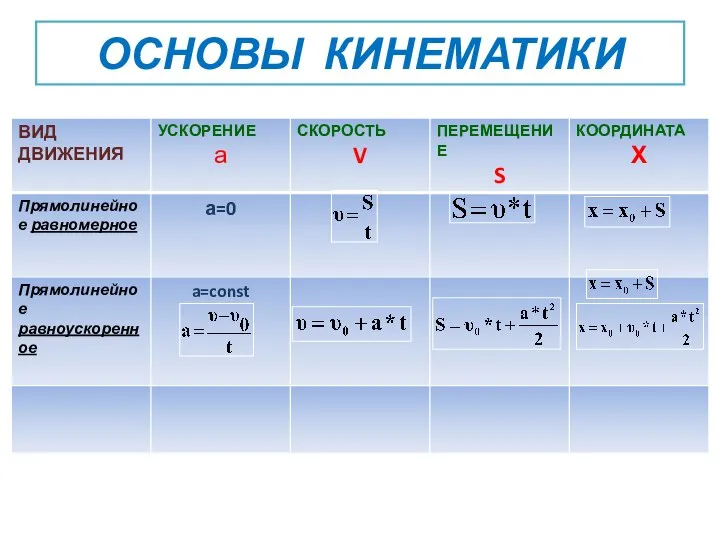 Основы кинематики
Основы кинематики Термодинамика. Работа идеального газа
Термодинамика. Работа идеального газа Движение тела по окружности
Движение тела по окружности Математическое моделирование кинетики химических реакций
Математическое моделирование кинетики химических реакций Передача контраста изображений, полученных с использованием лазерной системы видения
Передача контраста изображений, полученных с использованием лазерной системы видения Разборочно-сборочные работы рулевого механизма (червячного)
Разборочно-сборочные работы рулевого механизма (червячного) Презентация на тему Приливы, отливы, их использование 9 класс
Презентация на тему Приливы, отливы, их использование 9 класс  Склокомпозиційні матеріали для спаювання з широким інтервалом ТКЛР
Склокомпозиційні матеріали для спаювання з широким інтервалом ТКЛР Статика. Понятия и определения
Статика. Понятия и определения Виртуальный эксперимент на уроках физики
Виртуальный эксперимент на уроках физики Vztah mezi napětím a deformací fyzikální rovnice
Vztah mezi napětím a deformací fyzikální rovnice Презентация на тему Архимедова сила и плавание тел
Презентация на тему Архимедова сила и плавание тел  магнитное поле
магнитное поле Механическая работа и мощность
Механическая работа и мощность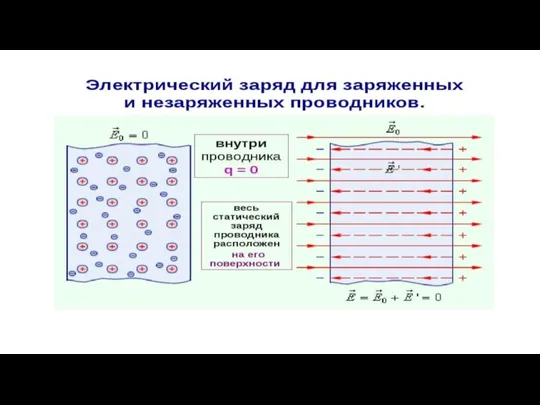 Распределение зарядов по поверхности проводника
Распределение зарядов по поверхности проводника Демонтаж тормозной системы автомобиля
Демонтаж тормозной системы автомобиля Тест КПП автомобиля
Тест КПП автомобиля Взвешивая время
Взвешивая время PRавый коронный, левый электронный. Рентген Попова или прибор захвативший весь мир
PRавый коронный, левый электронный. Рентген Попова или прибор захвативший весь мир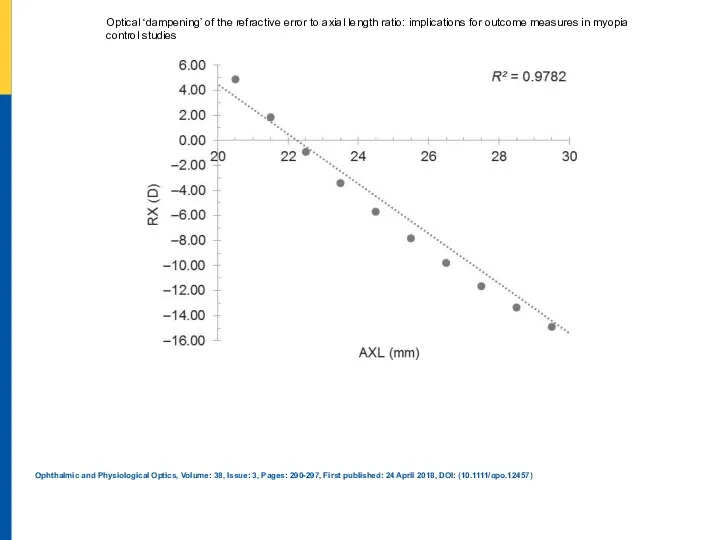 Ophthalmic and Physiological Optics, Volume
Ophthalmic and Physiological Optics, Volume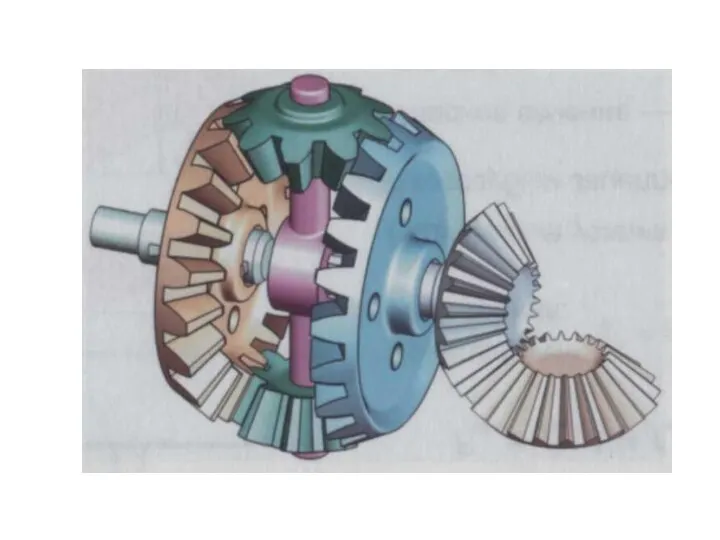 Виды конических зубчатых колес
Виды конических зубчатых колес Стримерлер - электрлік тесіп өтудің алдында атмосфералык қысым астында күшті электр өрісінде орналасқан газда кұралатын жіңішке
Стримерлер - электрлік тесіп өтудің алдында атмосфералык қысым астында күшті электр өрісінде орналасқан газда кұралатын жіңішке Урок 08 Магнітні властивості речовин. Гіпотеза Ампера(для дітей)
Урок 08 Магнітні властивості речовин. Гіпотеза Ампера(для дітей) Теория автоматического управления. Интегрирующие звенья
Теория автоматического управления. Интегрирующие звенья Энергия заряженного конденсата
Энергия заряженного конденсата Трансформатор и его принцип действия
Трансформатор и его принцип действия