Электростатика. Лекция 1

Свойства электрического заряда:
Двузначность.
Симметрия.
Квантованность.
Сохраняемость.
Инвариантность.
Электрический заряд – это свойство элементарных частиц.

Точечный электрический заряд – это заряженное тело, размеры которого много меньше расстояния до других тел.
Закон Кулона: сила взаимодействия двух точечных зарядов прямо пропорциональна величинам зарядов и обратно пропорциональна квадрату расстояния между ними. Сила направлена вдоль линии, соединяющей заряды.

В пространстве, окружающем электрический заряд, возникает электрическое поле.
Электростатическое поле-это электрическое поле, не изменяющееся со временем. Оно создаётся неподвижными электрическими зарядами.
Напряженность электрического поля – физическая величина, численно равна силе, действующей на единичный положительный заряд в данной точке поля.
В СИ размерность Е (В/м)

Напряженность поля точечного заряда
Направление вектора определяется направлением силы, действующей на положительный точечный заряд в данной точке поля

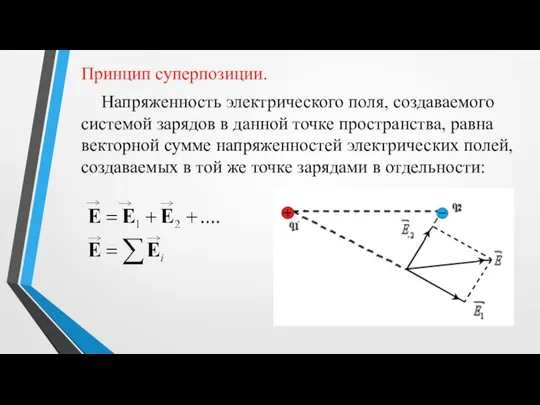
Принцип суперпозиции.
Напряженность электрического поля, создаваемого системой зарядов в данной точке пространства, равна векторной сумме напряженностей электрических полей, создаваемых в той же точке зарядами в отдельности:

По полученной картине можно легко судить о конфигурации данного электрического поля – о направлении и модуле вектора Е в разных точках поля.

Поток вектора напряжённости электрического поля через плоскую поверхность S в случае однородного поля
– это скалярная величина. Он может быть положительным, если cosα > 0 или отрицательным (cosα < 0).

Если поле неоднородно и поверхность не плоская

Теорема Гаусса для электростатического поля в вакууме
Для поверхности любой формы, если она замкнута и заключает в себе точечный заряд q, поток вектора Е равен
Теорема Гаусса для электростатического поля в вакууме: поток вектора напряженности электростатического поля в вакууме

В качестве замкнутой поверхности мыс-
ленно построим цилиндр, основания которого параллельны заряженной плоскости, а ось перпендикулярна ей. Так как образующие цилиндра параллельны линиям напряженности (cos α = 0), то поток вектора напряженности сквозь боковую поверхность цилиндра равен нулю.

Полный поток сквозь цилиндр равен сумме потоков сквозь его основания (площади оснований S равны и для основания Еn совпадает с Е), т.е. равен Ф = 2ES. Заряд, заключенный внутри построенной цилиндрической поверхности, равен σS.
Согласно теореме Гаусса
поле равномерно заряженной плоскости однородно.

Поле двух бесконечных параллельных разноименно заряженных плоскостей
Пусть плоскости заряжены равномерно разноименными зарядами с поверхностными плотностями +σ и -σ. Поле таких плоскостей найдем как суперпозицию (сумму) полей, создаваемых каждой из плоскостей в отдельности.
За пределами плоскостей поля вычитаются (линии напряженности направлены
навстречу друг другу),
поэтому здесь напряженность поля Е = 0.
В области между плоскостями Е = Е+ + Е_

Е+ и Е_ определяются по формуле
Поэтому результирующая напряженность
в 2 раза больше

Циркуляция вектора напряженности
электростатического поля
Пусть в электростатическом поле точечного заряда q из точки 1 в точку 2 вдоль произвольной траектории перемещается другой точечный заряд qo, тогда сила, приложенная к заряду qo, совершает работу. Работа силы F на элементарном перемещении dl равна

Работа при перемещении заряда qo из точки 1 в точку 2
Работа сил электростатического поля не зависит от траектории перемещения, а определяется только положениями начальной 1 и конечной 2 точек. Следовательно, электростатическое поле точечного заряда является потенциальным, а электростатические силы -
консервативными
Следствие: работа, совершаемая при перемещении
электрического заряда во внешнем электростатическом поле по любому замкнутому пути L, равна нулю!

Если перемещается единичный точечный положительный
заряд, то: L
Интеграл называется циркуляцией вектора напряженности. Таким образом, циркуляция вектора напряженности электростатического поля вдоль любого замкнутого контура равна нулю. Силовое поле, обладающее таким свойством, называется потенциальным. Из обращения в нуль циркуляции вектора Е следует, что линии напряженности электростатического поля не могут быть замкнутыми, они начинаются и кончаются на зарядах (соответственно на положительных или отрицательных) или же уходят в бесконечность.

Потенциал электростатического поля
Тело, находящееся в потенциальном поле сил, обладает
потенциальной энергией, за счет которой силами поля совершается работа. Работу сил электростатического поля
можно представить как разность потенциальных энергий, которыми обладает точечный заряд q0 в начальной и конечной точках траектории в поле заряда q
Потенциальная энергия заряда q0 в поле заряда q равна
Отношение потенциальной энергии заряда к величине заряда не зависит от qo и является энергетической характеристикой электростатического поля, называемой потенциалом φ:

Потенциал поля, создаваемого точечным зарядом q, равен
Работа, совершаемая силами электростатического поля при перемещении заряда q0 из точки 1 в точку 2, может быть представлена как
Разность потенциалов двух точек 1 и 2 в электростатическом поле определяется работой, совершаемой силами поля при перемещении единичного положительного заряда из точки 1 в точку 2.
Работа сил поля при перемещении единичного заряда q0 = 1 из точки 1 в точку 2 может быть записана также в виде

Пусть точка 2 удалена на бесконечно большое расстояние, где потенциал φ2 равен нулю, тогда работа сил электрического поля , а потенциал
Таким образом, потенциал — физическая величина, численно равная работе сил поля по перемещению единичного положительного заряда из данной точки поля на бесконечность.
Единица измерения потенциала и разности потенциалов — 1 вольт (В)

Напряженность как градиент потенциала.
Эквипотенциальные поверхности
Работа dA по перемещению единичного точечного положительного заряда из одной точки поля в другую вдоль оси х при условии, что точки расположены бесконечно близко друг к другу и x1 = x2 – dx равна dA = Exdx.
Та же работа равна φ1 - φ2 = - dφ. Приравняв оба выражения, можем записать
Повторив аналогичные рассуждения для осей у и z, можем найти вектор E:
где i, j, k — единичные векторы координатных осей x, y, z

Из определения градиента следует, что
Знак ≪—≫ определяется тем, что вектор напряженности Е поля направлен в сторону убывания потенциала.
Для графического изображения распределения потенциала электростатического поля, как и в случае поля тяготения, пользуются эквипотенциальными поверхностями —
поверхностями, во всех точках которых потенциал φ имеет одно и то же значение φ = const
Если поле создается точечным зарядом, то его потенциал равен
Таким образом, эквипотенциальные поверхности в данном
случае — концентрические сферы.

С другой стороны, линии напряженности в случае точечного заряда — радиальные прямые. Следовательно, линии напряженности в случае точечного заряда перпендикулярны эквипотенциальным поверхностям.