Содержание
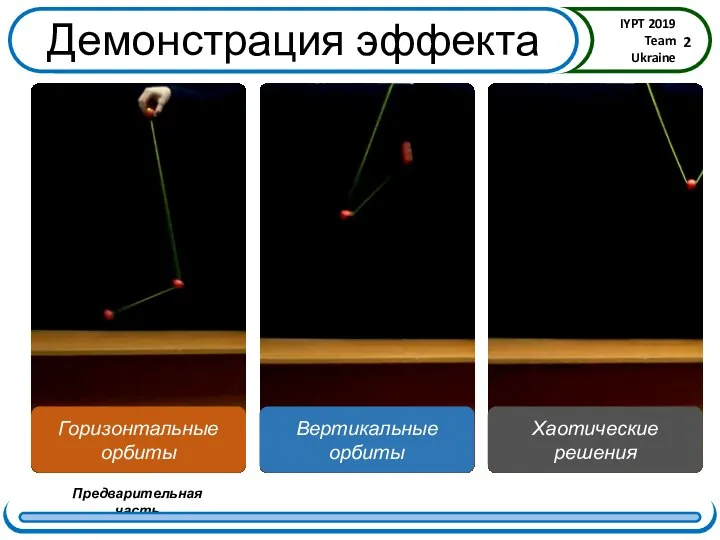
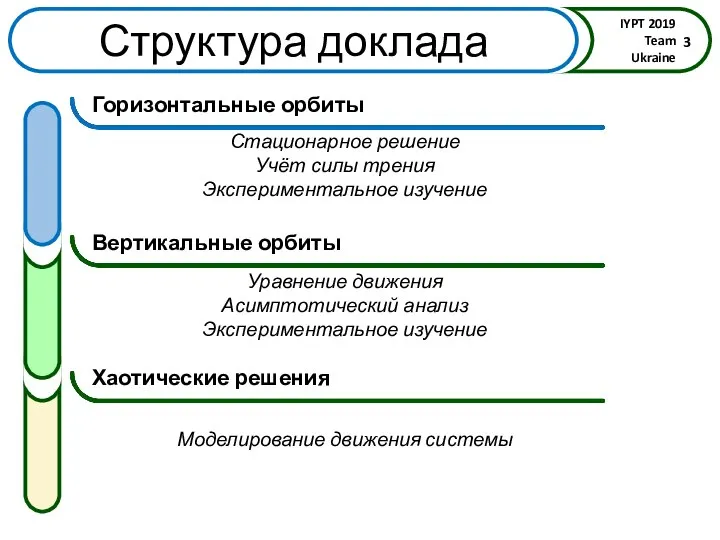
- 2. Демонстрация эффекта Горизонтальные орбиты Вертикальные орбиты Хаотические решения
- 4. Горизонтальные решения
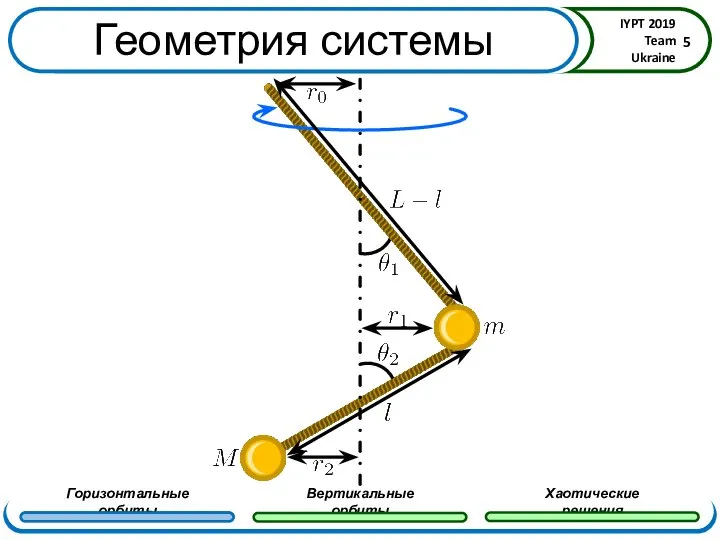
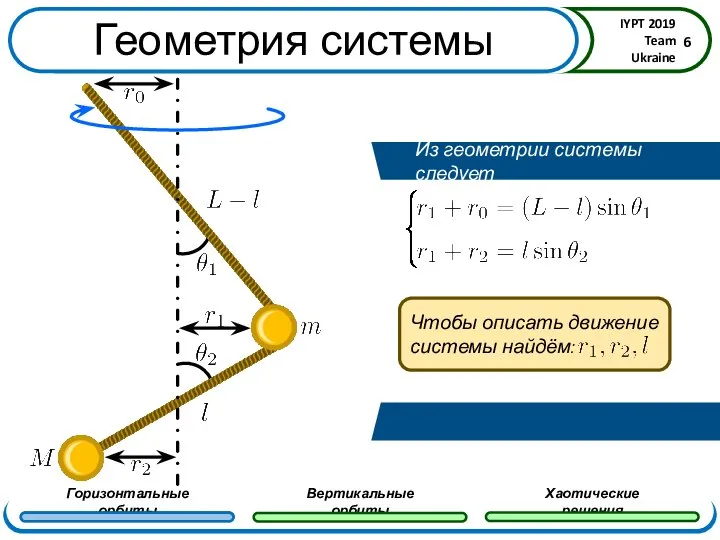
- 5. Геометрия системы
- 6. Геометрия системы Из геометрии системы следует
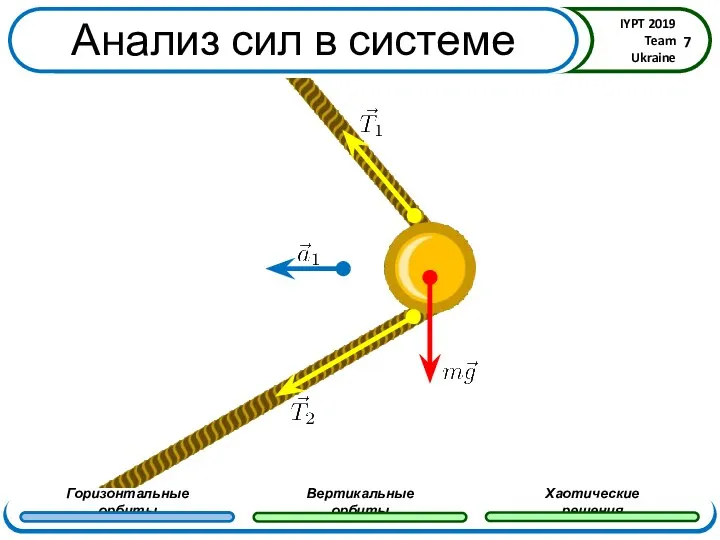
- 7. Анализ сил в системе Из геометрии системы следует
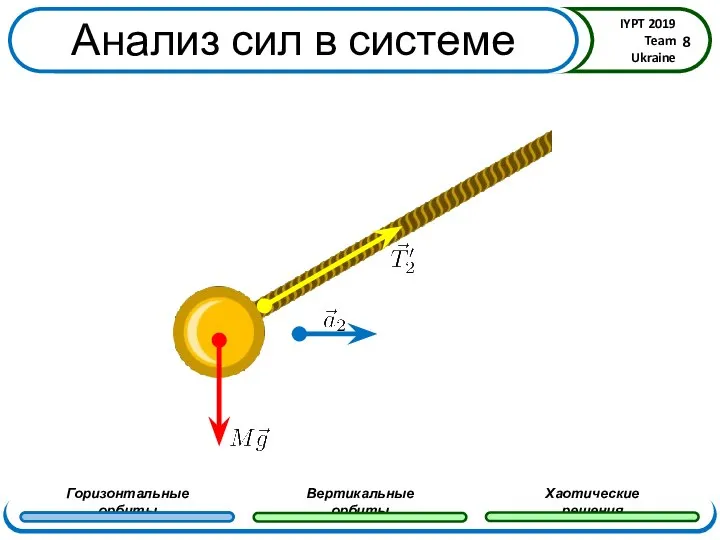
- 8. Анализ сил в системе
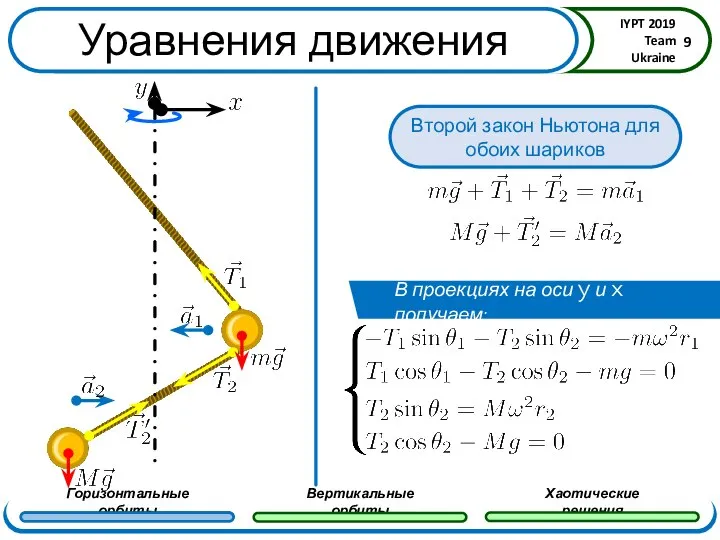
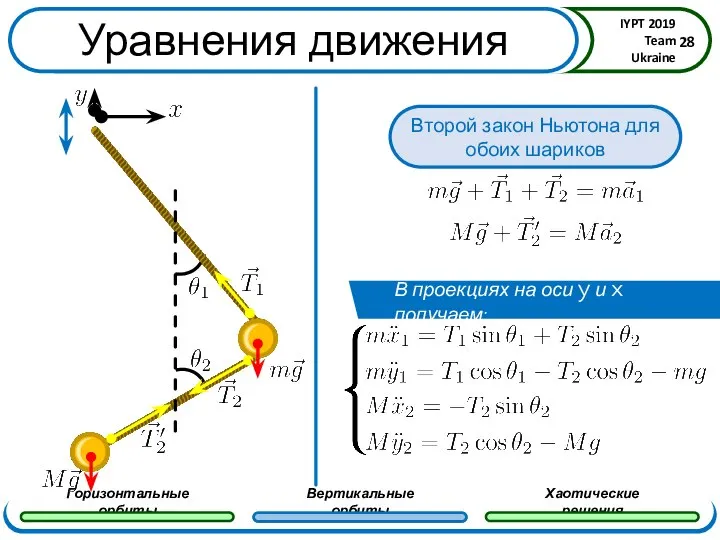
- 9. Уравнения движения В проекциях на оси y и x получаем:
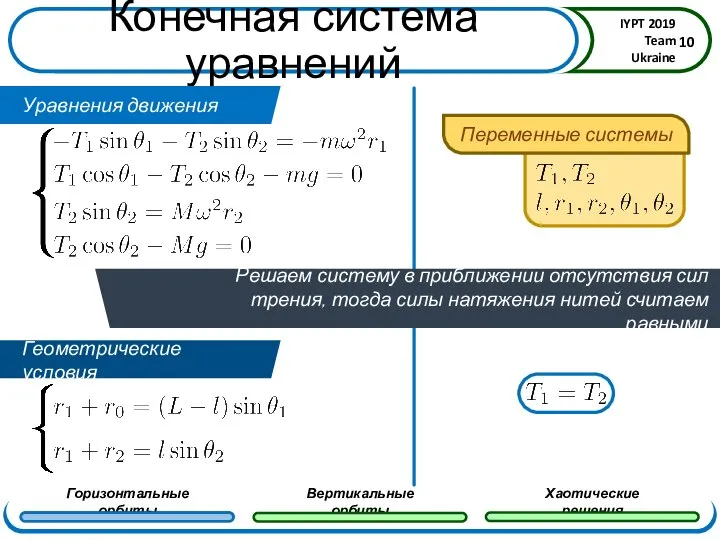
- 10. Конечная система уравнений В проекциях на оси y и x получаем: Геометрические условия Уравнения движения Переменные
- 11. Численное решение Геометрические условия Уравнения движения Решаем систему в приближении отсутствия сил трения, тогда силы натяжения
- 12. Численное решение
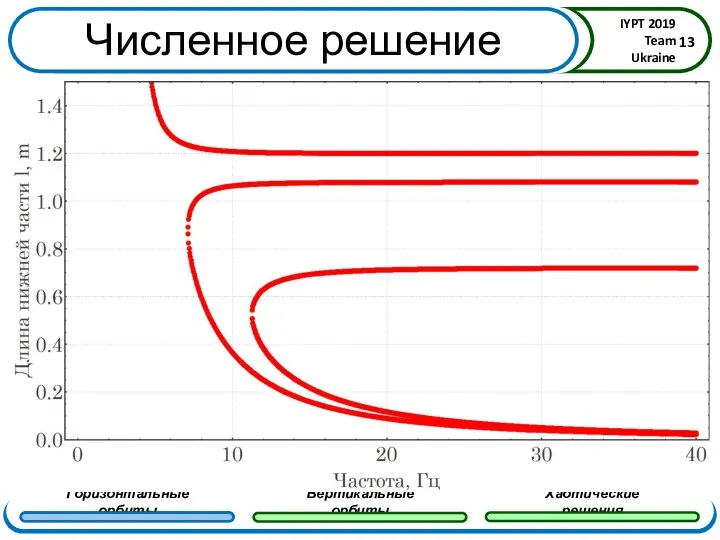
- 13. Численное решение
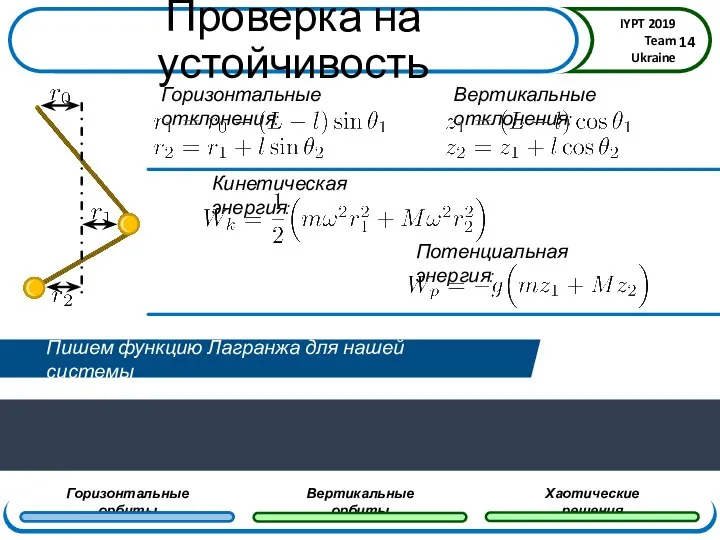
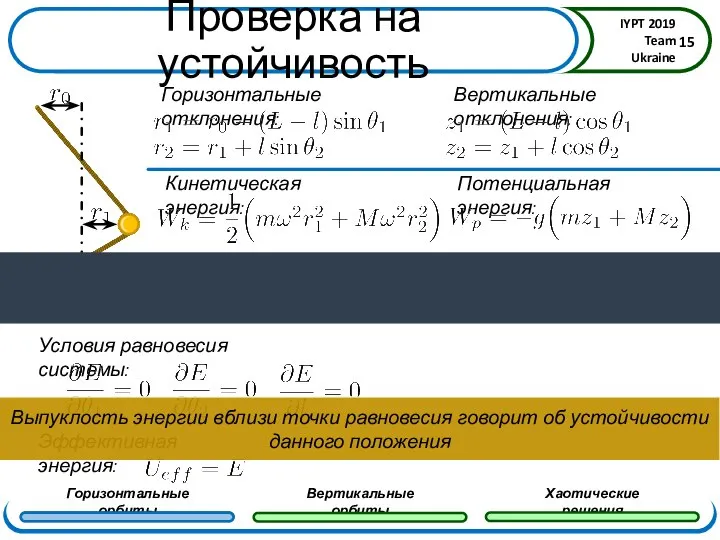
- 14. Проверка на устойчивость Пишем функцию Лагранжа для нашей системы
- 15. Проверка на устойчивость Пишем функцию Лагранжа для нашей системы Выпуклость энергии вблизи точки равновесия говорит об
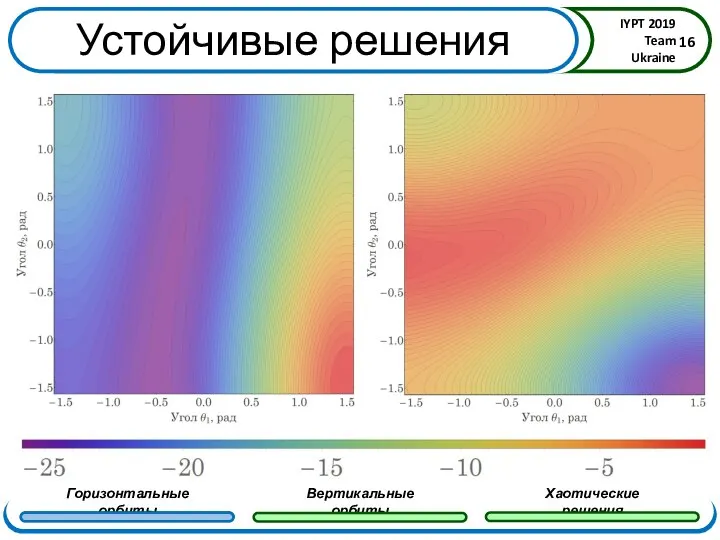
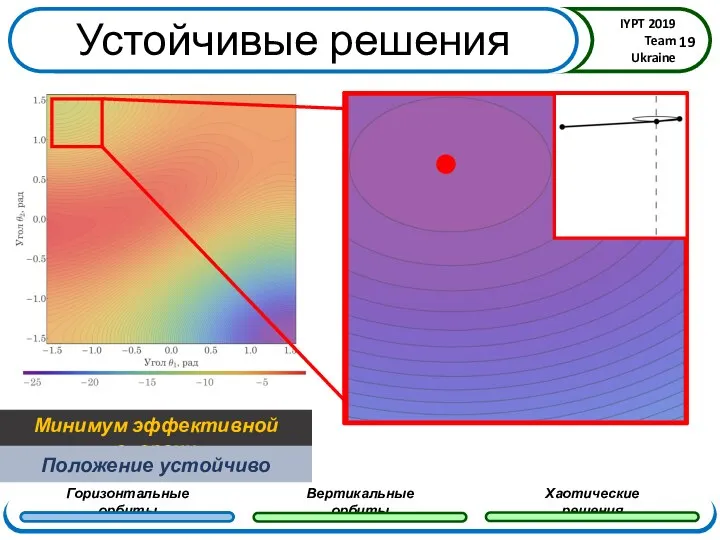
- 16. Устойчивые решения
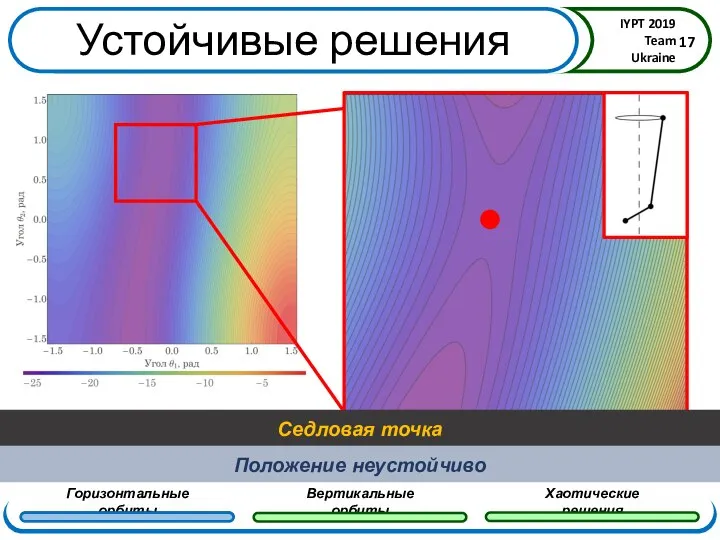
- 17. Устойчивые решения
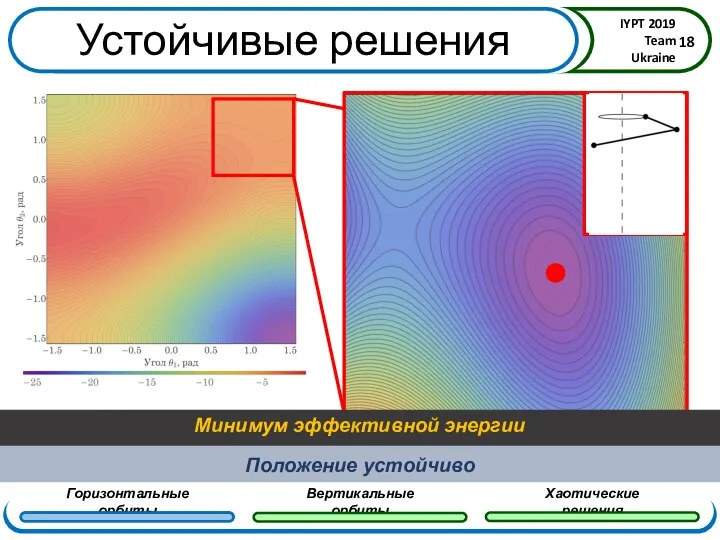
- 18. Устойчивые решения
- 19. Устойчивые решения
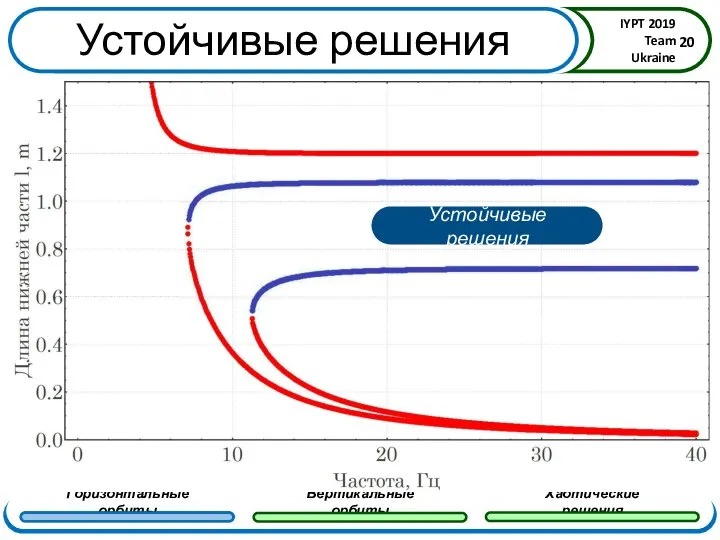
- 20. Устойчивые решения Устойчивые решения
- 21. Сила трения в системе В проекциях на оси y и x получаем: Геометрические условия Уравнения движения
- 22. Решение с учётом сил трения
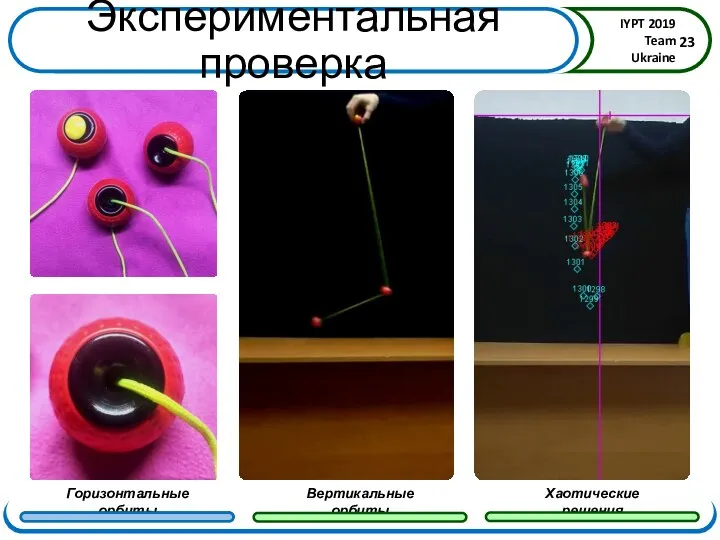
- 23. Экспериментальная проверка
- 24. Экспериментальная проверка
- 25. Вертикальные орбиты
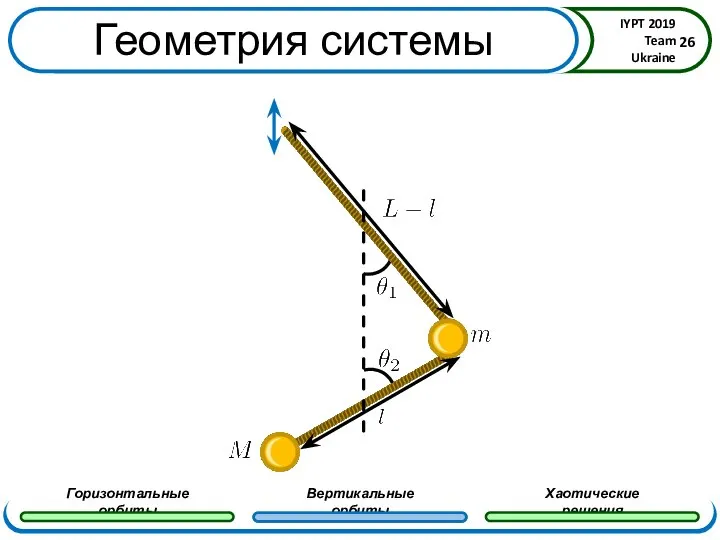
- 26. Геометрия системы
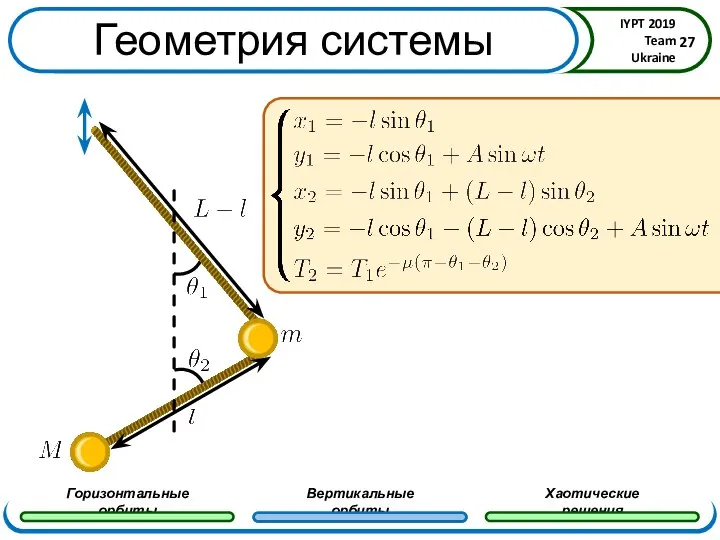
- 27. Геометрия системы
- 28. Уравнения движения В проекциях на оси y и x получаем:
- 29. Полная система уравнений В проекциях на оси y и x получаем:
- 30. Численное решение
- 31. Экспериментальная проверка
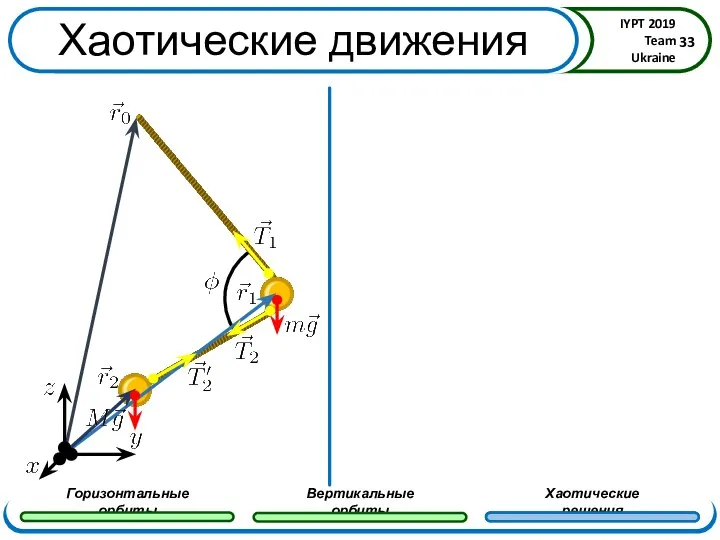
- 32. Хаотические решения
- 33. Хаотические движения
- 34. Что-то теоретическое…
- 35. Что-то экспериментальное…
- 36. 9. Шарики на нити Качественное и теоретическое изучение динамики движения системы Изучение устойчивости решений Экспериментальное изучение
- 37. 9. Шарики на нити Теоретическое изучение динамики движения системы Экспериментальная проверка решений Наденьте шарик со сквозным
- 38. 9. Шарики на нити Универсальная теоретическая модель для численной симуляции движения системы Наденьте шарик со сквозным
- 40. Скачать презентацию






 Электроемкость, конденсаторы
Электроемкость, конденсаторы Теплоусвоение внутренних поверхностей ограждающих конструкций
Теплоусвоение внутренних поверхностей ограждающих конструкций Классификация зубчатых передач
Классификация зубчатых передач Электромагнетизм
Электромагнетизм Энергия. Законы сохранения в механике
Энергия. Законы сохранения в механике Многофазные системы переменного тока. Преимущество трехфазной системы над однофазной
Многофазные системы переменного тока. Преимущество трехфазной системы над однофазной Деформация Сила упругости, закон Гука (Тема 1, Тема 2)
Деформация Сила упругости, закон Гука (Тема 1, Тема 2) Демонтаж устройства самообслуживания
Демонтаж устройства самообслуживания Излучение электромагнитного поля. Антенны
Излучение электромагнитного поля. Антенны Силы в механике
Силы в механике В мире занимательной физики. Интеллектуальный марафон
В мире занимательной физики. Интеллектуальный марафон Законы Ньютона
Законы Ньютона Механика. Комплексный экзамен
Механика. Комплексный экзамен Исследовательская работа по физике на тему: Искусственные источники света и их практическая ценность. Автор: Дуров Лев 9б класс Н
Исследовательская работа по физике на тему: Искусственные источники света и их практическая ценность. Автор: Дуров Лев 9б класс Н Реактивное движение
Реактивное движение Применение законов сохранения
Применение законов сохранения Электрическое поле. Постоянное электрическое поле. Франклинизация
Электрическое поле. Постоянное электрическое поле. Франклинизация Решение задач
Решение задач Ремонт трубопровода
Ремонт трубопровода Кинематика. Кинематика точки. Примеры
Кинематика. Кинематика точки. Примеры Вынужденные электромагнитные колебания
Вынужденные электромагнитные колебания Классификация тепловых двигателей
Классификация тепловых двигателей Использование электронных образовательных ресурсов в преподавании физики
Использование электронных образовательных ресурсов в преподавании физики Дополнительное оборудование
Дополнительное оборудование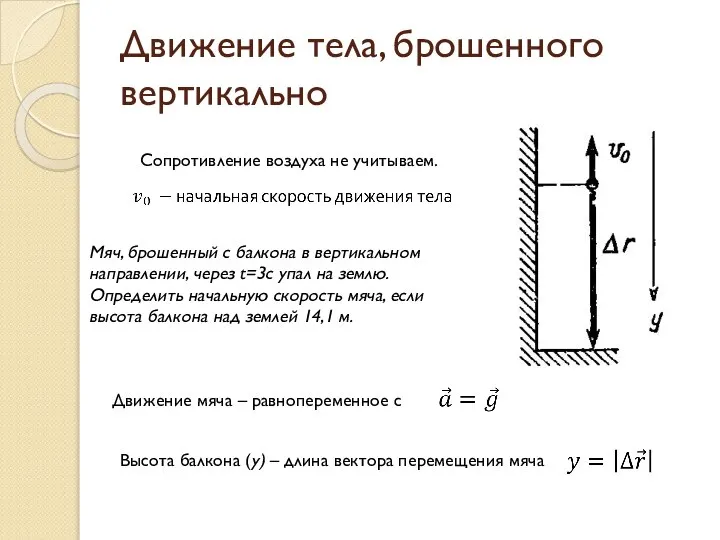 Движение тела, брошенного вертикально
Движение тела, брошенного вертикально История изобретения и развития тепловых двигателей
История изобретения и развития тепловых двигателей Программа расчета и проведение компьютерного моделирования прохождения электронов через многобарьерную потенциальную структуру
Программа расчета и проведение компьютерного моделирования прохождения электронов через многобарьерную потенциальную структуру Сила Архимеда
Сила Архимеда