Слайд 2 Физическая величина является понятием как минимум двух наук: физики и метрологии. По

определению физическая величина представляет собой некое свойство объекта, процесса, общее для целого ряда объектов по качественным параметрам, отличающееся, однако, в количественном отношении (индивидуальная для каждого объекта). Классическим примером иллюстрации этого определения служит тот факт, что, обладая собственной массой и температурой, все тела имеют индивидуальные числовые значения этих параметров. Соответственно размер физической величины считается ее количественным наполнением, содержанием, а в свою очередь значение физической величины представляет собой числовую оценку ее размеров.
Слайд 3Классификация физических величин:
1) активные и пассивные физические величины – при делении по отношению

к сигналам измерительной информации.
Причем первые (активные) в данном случае представляют собой величины, которые без использования вспомогательных источников энергии имеют вероятность быть преобразованными в сигнал измерительной информации. А вторые (пассивные) представляют собой такие величины, для измерения которых нужно использовать вспомогательные источники энергии, создающие сигнал измерительной информации;
Слайд 42) аддитивные (или экстенсивные) и неаддитивные (или интенсивные) физические величины – при делении

по признаку аддитивности.
Считается, что первые (аддитивные) величины измеряются по частям, кроме того, их можно точно воспроизводить с помощью многозначной меры, основанной на суммировании размеров отдельных мер. А вторые (неаддитивные) величины прямо не измеряются, так как они преобразуются в непосредственное измерение величины или измерение путем косвенных измерений.
Слайд 5Этапы развития систем физических величин
В 1791 г. Национальным собранием Франции была принята первая

в истории система единиц физических величин. Она представляла собой метрическую систему мер. В нее входили: единицы длин, площадей, объемов, вместимостей и веса. А в их основу были положены две общеизвестные ныне единицы: метр и килограмм. Ряд исследователей считают, что, строго говоря, эта первая система не является системой единиц в современном понимании. И лишь в 1832 г. немецким математиком К. Гауссом была разработана и опубликована новейшая методика построения системы единиц, представляющая собой в данном контексте некую совокупность основных и производных единиц.
Слайд 61) система СГС (1881 г.) или Система единиц физических величин СГС, основными единицами которых являются

следующие: сантиметр (см) – представленный в виде единицы длины, грамм (г) – в виде единицы массы, а также секунда (с) – в виде единицы времени;
Слайд 72) система МКГСС (конец ХIХ в.), использующая первоначально килограмм как единицу веса, а впоследствии как

единицу силы, что вызвало создание системы единиц физических величин, основными единицами которой стали три физических единицы: метр как единица длины, килограмм—сила как единица силы и секунда как единица времени;
Слайд 83) система МКСА (1901 г.), основы которой были созданы итальянским ученым Дж. Джорджи, который предложил

в качестве единиц системы МКСА метр, килограмм, секунду и ампер.
Слайд 9Синим не пишем, а читаем. На сегодняшний день в мировой науке существует

неисчислимое количество всевозможных систем единиц физических величин, а также немало так называемых внесистемных единиц. Это, конечно, приводит к определенным неудобствам при вычислениях, вынуждая прибегать к пересчету при переводе физических величин из одной системы единиц в другую. Сложилась ситуация, при которой возникла серьезная необходимость унификации единиц измерения. Требовалось создать такую систему единиц физических величин, которая подходила бы для большинства различных отраслей области измерений. Причем в роли главного акцента должен был звучать принцип когерентности, подразумевающий под собой, что единица коэффициента пропорциональности равна в уравнениях связи между физическими величинами.
4) Система СИ (единая Международная система единиц) - проект созданный в 1954 г.
Он носил название «проект Международной системы единиц» и был в конце концов утвержден Генеральной конференцией по мерам и весам. Таким образом, система, основанная на семи основных единицах, стала называться Международной системой единиц, или сокращенно СИ, что происходит от аббревиатуры французского наименования «Sуstеmе Intеrnаtiоnаl* (SI).
Слайд 10Международная система единиц или СИ.
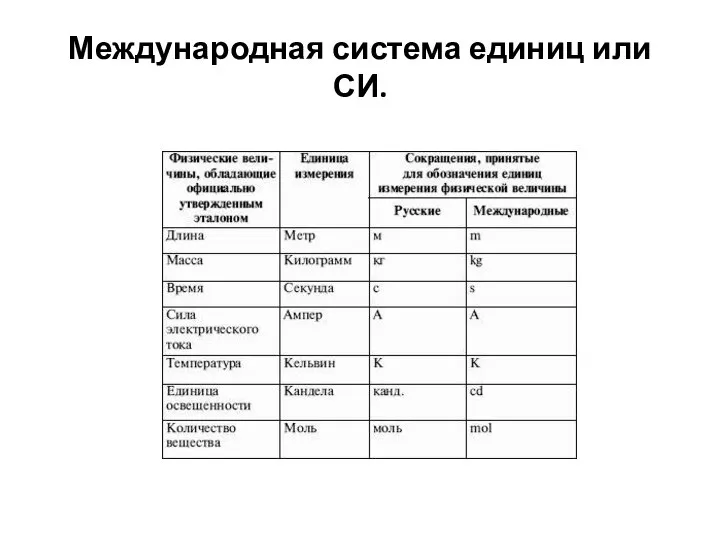
Слайд 11 Решениями Генеральной конференции по мерам и весам приняты такие определения основных единиц

измерения физических величин:
метр считается длинной пути, который проходит свет в вакууме за 1/299 792 458 долю секунды;
килограмм считается приравненным к существующему международному прототипу килограмма;
секунда равна 919 2631 770 периодам излучения, соответствующего тому переходу, который происходит между двумя так называемыми сверхтонкими уровнями основного состояния атома Сs133;
ампер считается мерой той силы неизменяющегося тока, вызывающего на каждом участке проводника длиной 1 м силу взаимодействия при условии прохождения по двум прямолинейным параллельным проводникам, обладающим такими показателями, как ничтожно малая площадь кругового сечения и бесконечная длина, а также расположение на расстоянии в 1 м друг от друга в условиях вакуума;
кельвин равен 1/273,16 части термодинамической температуры, так называемой тройной точки воды;
моль равен количеству вещества системы, в которую входит такое же количество структурных элементов, что и в атомы в С 12 массой 0,012 кг.
Слайд 12Кроме того, Международная система единиц содержит две достаточно важные дополнительные единицы, необходимые

для измерения плоского и телесного углов. Так, единица плоского угла – это радиан, или сокращенно рад, представляющий собой угол между двух радиусов окружности, длина дуги между которыми равняется радиусу окружности. Если речь идет о градусах, то радиан равен 57°17 48 '.
А стерадиан, или ср, принимаемый за единицу телесного угла, представляет собой, соответственно, телесный угол, расположение вершины которого фиксируется в центре сферы, а площадь, вырезаемая данным углом на поверхности сферы, равна площади квадрата, сторона которого равна длине радиуса сферы











 Тема 10. Схема устройства и принцип работы ПД
Тема 10. Схема устройства и принцип работы ПД Звуковые волны
Звуковые волны Потенциальная энергия заряженного тела в однородном электростатическом поле. Потенциал. Разность потенциалов
Потенциальная энергия заряженного тела в однородном электростатическом поле. Потенциал. Разность потенциалов Центр тяжести.Виды равновесия (10 класс)
Центр тяжести.Виды равновесия (10 класс) Электризация
Электризация Термообработка сталей
Термообработка сталей Найдем правильную дорогу
Найдем правильную дорогу Заняття 4 251
Заняття 4 251 Сила тока. Единицы силы тока. Амперметр
Сила тока. Единицы силы тока. Амперметр Погрешности измерения. 7 класс
Погрешности измерения. 7 класс Протонно-нейтронная модель ядра. Физический смысл зарядового и массового чисел. Изотопы
Протонно-нейтронная модель ядра. Физический смысл зарядового и массового чисел. Изотопы Формирование понятия энергия
Формирование понятия энергия Школа юного исследователя
Школа юного исследователя Механические передачи
Механические передачи Основные определения
Основные определения Задачи по физике
Задачи по физике Презентация на тему Дифракция света
Презентация на тему Дифракция света  Барометр-анероид. Атмосферное давление на различных высотах. Физика 7 класс
Барометр-анероид. Атмосферное давление на различных высотах. Физика 7 класс قانون گاوس :کل شار الکتریکی که از یک سطح بسته عبور میکند،
قانون گاوس :کل شار الکتریکی که از یک سطح بسته عبور میکند،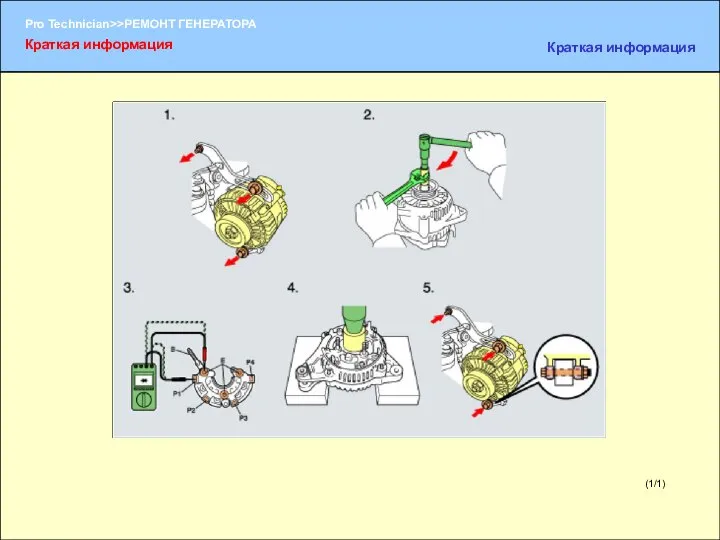 Ремонт генератора
Ремонт генератора Явление электромагнитной индукции
Явление электромагнитной индукции Переменный ток
Переменный ток Циклы Карно
Циклы Карно Законы постоянного тока
Законы постоянного тока Решение задач по кинематики
Решение задач по кинематики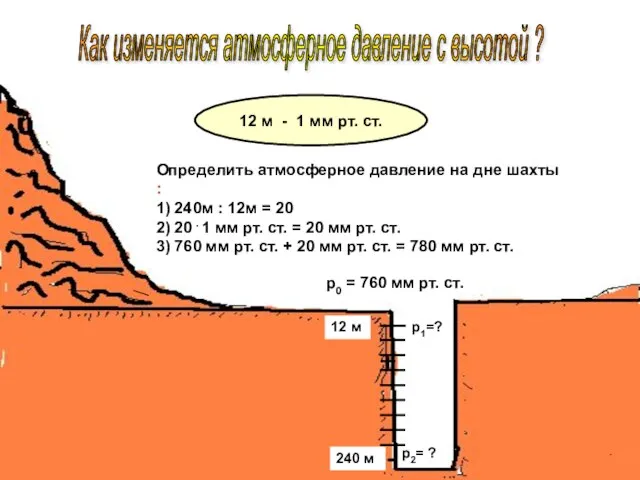 Презентация по физике "Как изменяется атмосферное давление с высотой ?" -
Презентация по физике "Как изменяется атмосферное давление с высотой ?" -  Норийные ковши, скребки, ролики (пластиковые) для цепных транспортеров
Норийные ковши, скребки, ролики (пластиковые) для цепных транспортеров Термодинамика. Работа идеального газа
Термодинамика. Работа идеального газа