Содержание
- 2. Бесконечная монохроматическая волна, уравнение которой имеет вид не может быть использована для передачи информации.
- 3. Для того, чтобы волна могла переносить информацию, необходимо изменять со временем (модулировать) её параметры А, ω
- 4. Рассмотрим волну с амплитудной модуляцией. Для того, чтобы создавать волну, амплитуда которой изменяется со временем, источник
- 5. Ранее было показано, что биения возникают при сложении двух однонаправленных гармонических колебаний, частоты которых ω1 и
- 6. Обе волны возбуждают одинаково направленные колебания в одних и тех же точках пространства. Получим уравнение результирующей
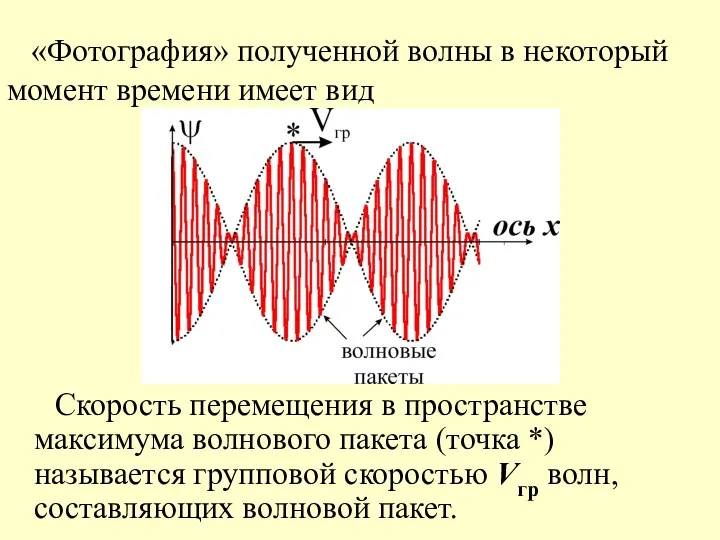
- 8. «Фотография» полученной волны в некоторый момент времени имеет вид Скорость перемещения в пространстве максимума волнового пакета
- 9. Огибающая волнового пакета определяется в уравнении модулированной волны членом
- 10. В процессе перемещения такой модулированной волны для точки, обозначенной звездочкой (*), постоянной остается фаза, стоящая в
- 11. Поставим задачу: выразить групповую скорость Vгр через циклические частоты ω1, ω2 и волновые числа k1, k2
- 12. Итак, показано, что групповая скорость волн равна производной от циклической частоты по волновому числу: Поставим задачу:
- 13. Итак, показано, что групповая скорость волны выражается через фазовую скорость формулой
- 14. Рассмотрим три случая: 1) Vф ≠ f(λ) – фазовая скорость не зависит от длины волны (явление
- 15. 2) Vф растет с ростом длины волны λ, то есть (наблюдается нормальная дисперсия);
- 16. 3) Vф уменьшается с ростом длины волны λ, то есть (наблюдается аномальная дисперсия).
- 17. Итак, если дисперсия отсутствует, то групповая скорость волн равна фазовой если наблюдается нормальная дисперсия, то групповая
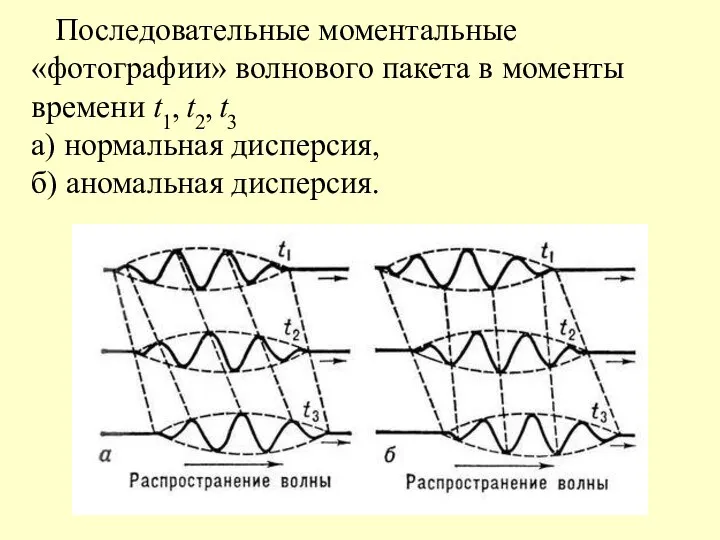
- 18. Последовательные моментальные «фотографии» волнового пакета в моменты времени t1, t2, t3 а) нормальная дисперсия, б) аномальная
- 19. График зависимости циклической частоты волны от волнового числа ω=f(k) называется дисперсионным.
- 21. Скачать презентацию





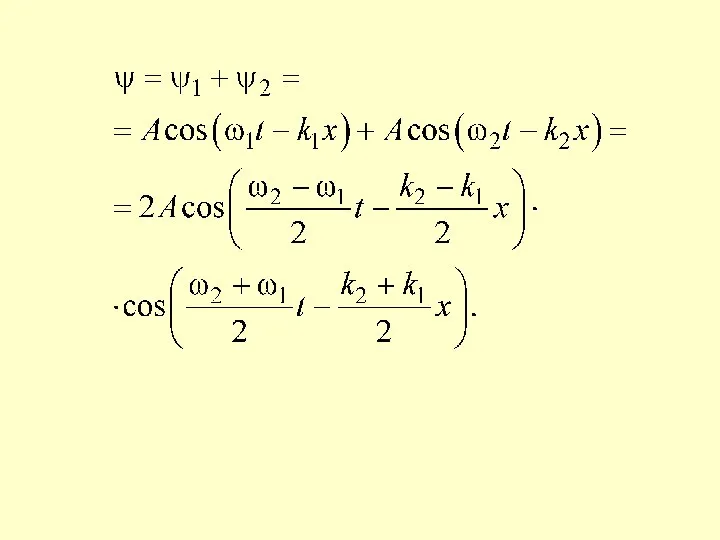










 Электрокинетические явления
Электрокинетические явления Теоретический чертеж. Координатные оси
Теоретический чертеж. Координатные оси Основные понятия, определения и законы электромеханики
Основные понятия, определения и законы электромеханики Телескопи. Типи телескопів за розташуванням
Телескопи. Типи телескопів за розташуванням M_P_Rezistivnye_M (1)
M_P_Rezistivnye_M (1) Презентация Механика Лекция 1
Презентация Механика Лекция 1 Резистор. Функциональное назначение резистра
Резистор. Функциональное назначение резистра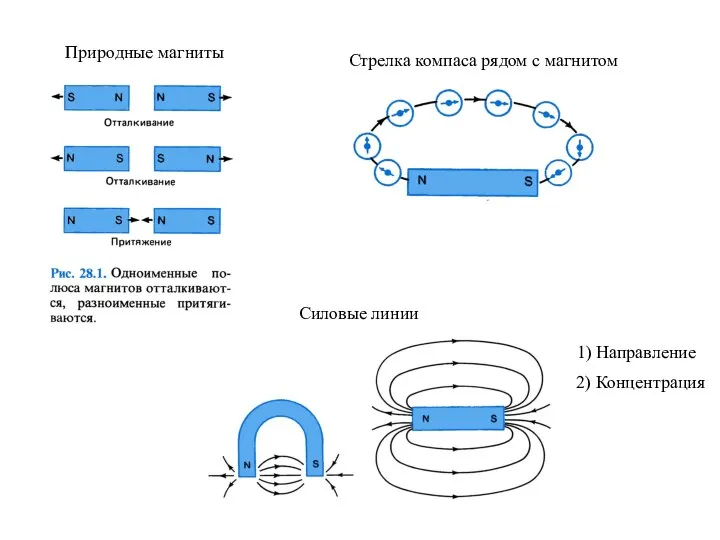 Природные магниты
Природные магниты L2_1_Mekhanicheskie_kharakteristiki_metallov
L2_1_Mekhanicheskie_kharakteristiki_metallov Реостаты
Реостаты Оптимизация методики разделения лечебного препарата Clopidogrel Hydrogen Sulfate с сопутствующей примесью (А)
Оптимизация методики разделения лечебного препарата Clopidogrel Hydrogen Sulfate с сопутствующей примесью (А) Интерактивная игра по физике Эрудит. Для учащихся 7 класса
Интерактивная игра по физике Эрудит. Для учащихся 7 класса Изменения агрегатных состояний вещества. Физический диктант
Изменения агрегатных состояний вещества. Физический диктант Решение задач на расчёт КПД теплового двигателя. 8 класс
Решение задач на расчёт КПД теплового двигателя. 8 класс Методы обзора пространства и измерения координат
Методы обзора пространства и измерения координат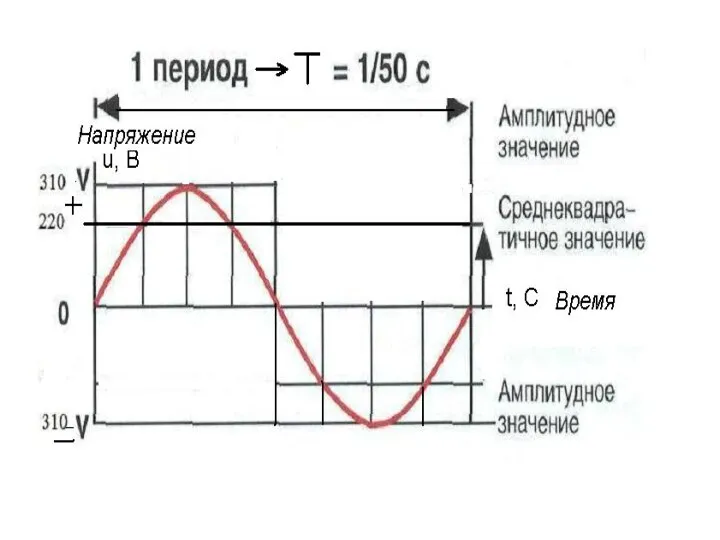 Действующее и среднее значение синусоидального тока
Действующее и среднее значение синусоидального тока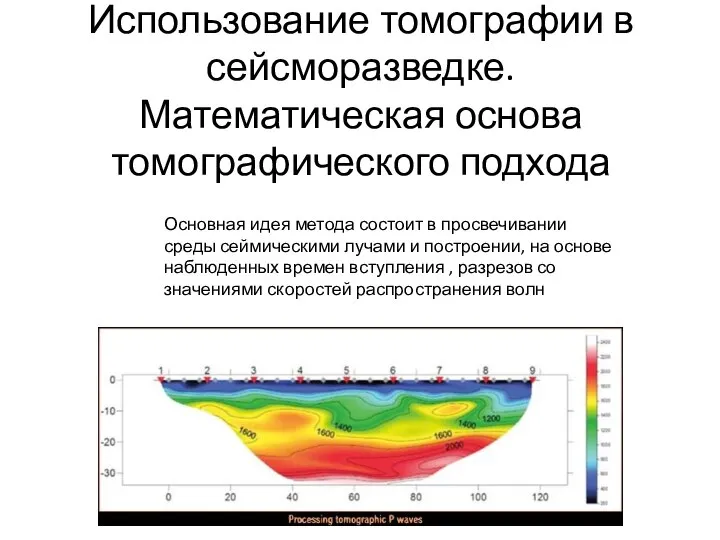 Использование томографии в сейсморазведке. Математическая основа томографического подхода
Использование томографии в сейсморазведке. Математическая основа томографического подхода Закон Ома для участка цепи
Закон Ома для участка цепи Давление газа
Давление газа Основные положения технической термодинамики
Основные положения технической термодинамики Ток, протекающий в нейтралях трансформаторов и автотрансформаторов при КЗ на землю
Ток, протекающий в нейтралях трансформаторов и автотрансформаторов при КЗ на землю Физика на рыбалке
Физика на рыбалке Инерция в жизни человека
Инерция в жизни человека Движение жидкостей и газов. Закон Бернулли
Движение жидкостей и газов. Закон Бернулли Динамика. Законы механики Ньютона
Динамика. Законы механики Ньютона Переменный ток
Переменный ток В мире звуков
В мире звуков Реактивное движение
Реактивное движение