Колебания систем со многими степенями свободы

Колебания без трения и при наличии трения
Автоколебательные системы
Колебания без затухания и при наличии затухания
Вынужденные колебания
СОДЕРЖАНИЕ

Колебаниями называют движение или процессы, которые характеризуются определенной повторяемостью во времени.
Свободные колебания – те колебания, которые совершаются за счёт первоначально сообщенной энергии при последующем отсутствии воздействия внешних сил на колебательную систему.
Гармонические колебании
x = Asin(ω0t+φ0)
ω0 – циклическая частота – число полных колебаний, которые совершаются за 2П единиц времени φ=2πν
T=2π/ω – период колебаний.
КОЛЕБАНИЯ БЕЗ ТРЕНИЯ И ПРИ НАЛИЧИИ ТРЕНИЯ

Колебания при наличии трения.
Затуханием колебаний называется постепенное ослабление колебаний с течением времени, обусловленное потерей энергии колебательной системой. Свободные колебания реальных систем всегда затухают. Затухание свободных механических колебаний вызывается главным образом трением и возбуждением в окружающей среде упругих волн.
Колебания в отсутствие трения (сопротивления среды) являются гармоническими. Примерами свободных гармонических колебаний служат колебания систем под действием упругих или квазиупругих сил. Частота свободных колебаний системы в отсутствие сил трения и сопротивления среды называются собственной частотой механической системы.
Назад

АВТОКОЛЕБАТЕЛЬНЫЕ СИСТЕМЫ

На рисунке показана схема механизма маятниковых часов. На ось храпового колеса A (которое в этой системе выполняет функцию нелинейного регулятора) действует постоянный момент силы M, передающийся через зубчатую передачу от заводной пружины или от гири. При вращении колеса A его зубцы сообщают кратковременные импульсы силы маятнику P (осциллятору), благодаря которым его колебания не затухают.
Назад

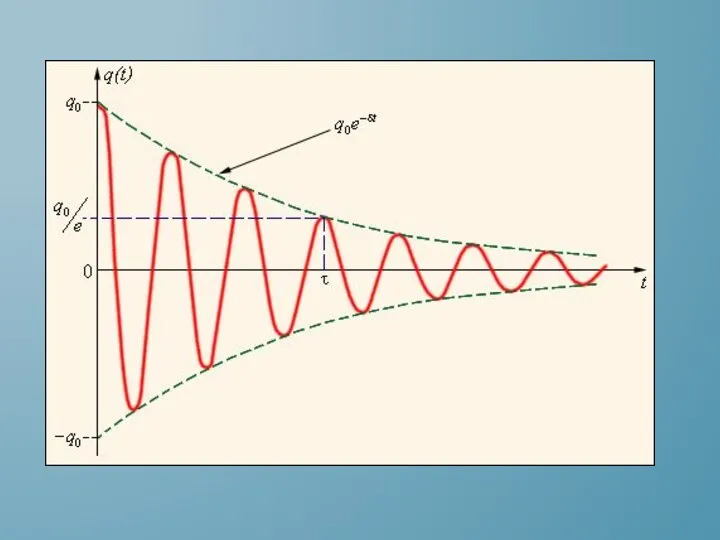
КОЛЕБАНИЯ БЕЗ ЗАТУХАНИЯ И ПРИ НАЛИЧИИ ЗАТУХАНИЯ
Затухающими колебаниями называются свободные колебания механической системы при наличии сил трения или сил сопротивления среды.
Если убыль энергии не восполняется за счёт работы внешних сил, колебания будут затухать. При этом механическая энергия переходит в теплоту. Механическая модель системы, совершающей затухающие механические колебания, приведена на рисунке: материальная точка массой m, колеблющаяся в вязкой среде под действием упругой Fупр (или квазиупругой) силы и силы сопротивления Fсопр вдоль некоторой оси x.
Выражение называется дифференциальным уравнением
затухающих колебаний.

В зависимости от соотношений между величинами β и ω0 существует три типа решений уравнения:
если β < ω0 - затухающие колебания,
если β << ω0 - слабое затухание,
если β > ω0 - сильное затухание.
График зависимости x = f (t) при затухающих колебаниях изображен на рисунке.

ХАРАКТЕРИСТИКИ ЗАТУХАЮЩИХ КОЛЕБАНИЙ.

Назад

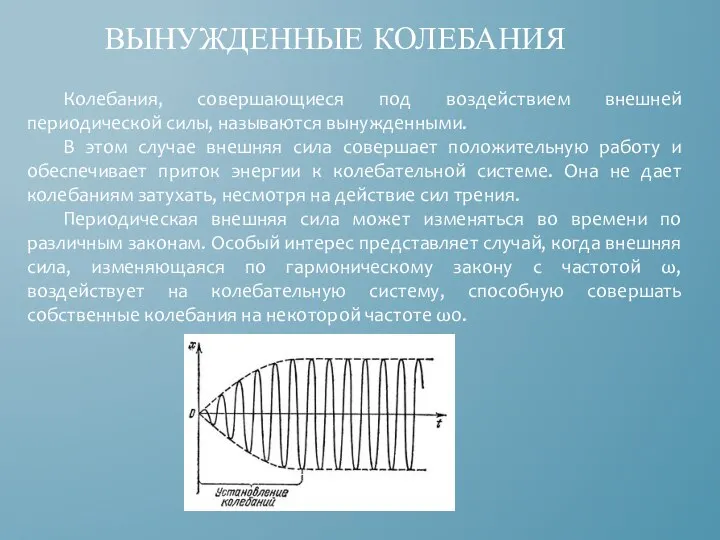
ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ
Колебания, совершающиеся под воздействием внешней периодической силы, называются вынужденными.
В этом случае внешняя сила совершает положительную работу и обеспечивает приток энергии к колебательной системе. Она не дает колебаниям затухать, несмотря на действие сил трения.
Периодическая внешняя сила может изменяться во времени по различным законам. Особый интерес представляет случай, когда внешняя сила, изменяющаяся по гармоническому закону с частотой ω, воздействует на колебательную систему, способную совершать собственные колебания на некоторой частоте ω0.

Допустим, что механическая колебательная система подвергается действию внешней силы, изменяющейся со временем по гармоническому закону:
(2.1)
В этом случае уравнение второго закона Ньютона имеет вид
Введя обозначения , преобразуем, уравнение приобретёт вид:
(2.2)
Здесь β — коэффициент затухания, ω0 — собственная частота колебательной системы, ω — частота вынуждающей силы.
Дифференциальное уравнение (2.2) описывает вынужденные колебания.
Назад