Слайд 210.1. Первообразная
https://youtu.be/3vR27xG0pcI

Слайд 3
Правила вычисления производной

Слайд 4Взаимно обратные операции:
— умножение – деление;
— извлечение квадратного корня – возведение в

квадрат;
— дифференцирование – интегрирование.
Слайд 1010.2. Правила отыскания первообразных
https://youtu.be/hBo3KcfLScw

Слайд 11Дифференцирование – процесс нахождения производной функции, интегрирование – процесс нахождения функции по

данной производной.
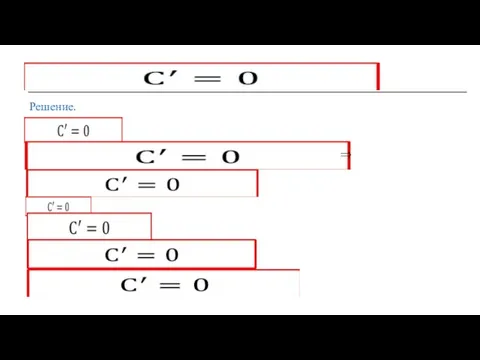
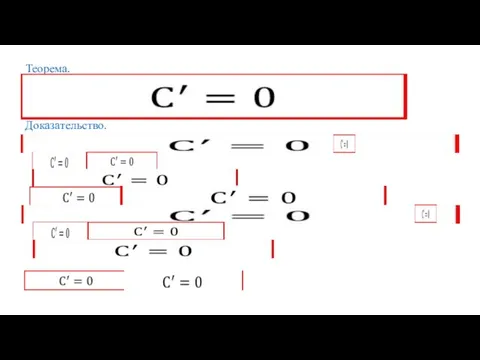
Слайд 13Первообразная суммы равна сумме первообразных.
Правило 1.

Слайд 15Постоянный множитель выносится за знак первообразной.
Правило 2.

Слайд 17Правило нахождения производной сложной функции:

Слайд 2110.3. Неопределённый интеграл
https://youtu.be/tuYbRdyJz_Y

Слайд 22Первообразная суммы равна сумме первообразных.
Правило 1.
Постоянный множитель выносится за знак первообразной.
Правило 2.
Правило

3.




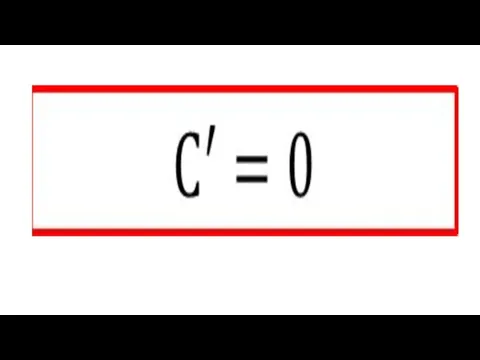
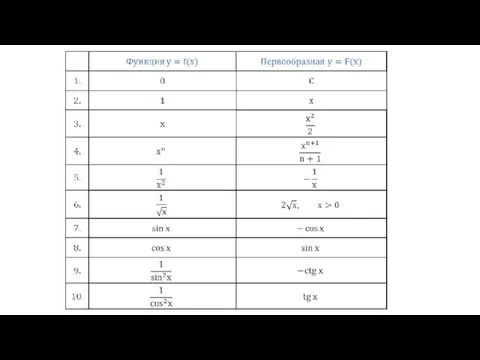






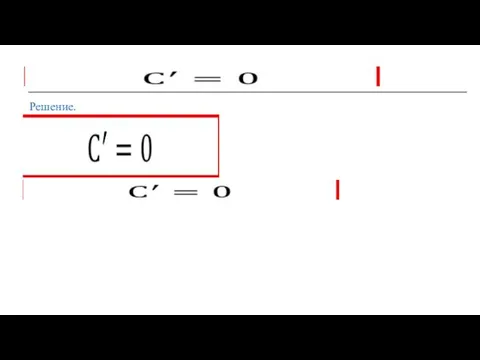




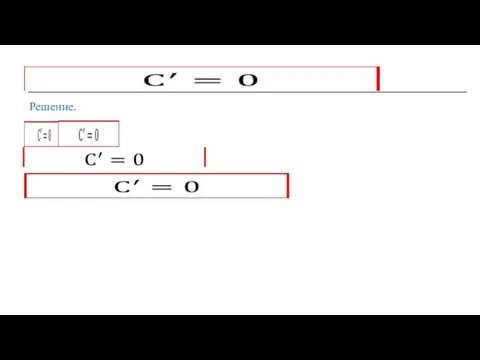




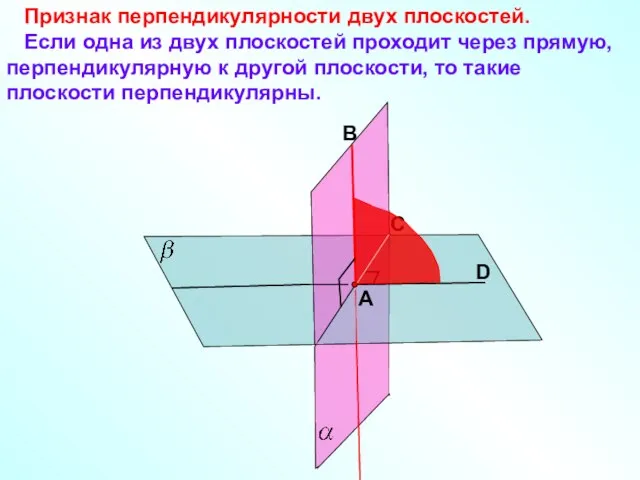 Признак перпендикулярности двух плоскостей
Признак перпендикулярности двух плоскостей Признаки равенства треугольников
Признаки равенства треугольников Уравнение плоскости
Уравнение плоскости Замена переменных в двойных интегралах
Замена переменных в двойных интегралах Золотое сечение
Золотое сечение Число 0. Цифра 0
Число 0. Цифра 0 Решение задач на временные отношения (подготовка к олимпиаде по математике обучающихся 4 класса)
Решение задач на временные отношения (подготовка к олимпиаде по математике обучающихся 4 класса) Перпендикуляр и наклонные. Угол между прямой и плоскостью
Перпендикуляр и наклонные. Угол между прямой и плоскостью Презентация на тему Задачи группы В 12
Презентация на тему Задачи группы В 12  Умножение пяти, на 5 и соответствующие случаи деления. Математика 3 класс. Учителя начальных классов Лаишевской специальной школ
Умножение пяти, на 5 и соответствующие случаи деления. Математика 3 класс. Учителя начальных классов Лаишевской специальной школ Комбинаторная задача с шарами
Комбинаторная задача с шарами Элементы теории вероятностей и математической статистики
Элементы теории вероятностей и математической статистики Противоположные числа и модуль
Противоположные числа и модуль Теоремы сложения и умножения вероятностей. Вероятность противоположного события
Теоремы сложения и умножения вероятностей. Вероятность противоположного события Возможности символьного вычисления в среде MatLab
Возможности символьного вычисления в среде MatLab Признаки равенства треугольников
Признаки равенства треугольников Задачи на построение
Задачи на построение Сложение и вычитание десятичных дробей
Сложение и вычитание десятичных дробей Сфера, описанная вокруг многогранника
Сфера, описанная вокруг многогранника Элективный курс. Алгебра 11 класс. Уроки 07-08
Элективный курс. Алгебра 11 класс. Уроки 07-08 Презентация на тему Устный счет на уроках математики
Презентация на тему Устный счет на уроках математики  Теорема, обратная теореме Пифагора
Теорема, обратная теореме Пифагора Сравнение, сложение и вычитание дробей с разными знаменателями
Сравнение, сложение и вычитание дробей с разными знаменателями Методичні основи вивчення часу і одиниць його вимірювання
Методичні основи вивчення часу і одиниць його вимірювання Интегральная оценка угрозы биотерроризма. Цели, методы, задачи
Интегральная оценка угрозы биотерроризма. Цели, методы, задачи Уравнение окркжности
Уравнение окркжности Сумматор. Таблица истинности сумматора
Сумматор. Таблица истинности сумматора Многозначные числа. Тест
Многозначные числа. Тест