представляет интерес для целого ряда приложений, например, для повышения эффективности просветляющих и поглощающих покрытий в радиодиапазоне, разработки радиопрозрачных обтекателей для антенн, объяснения механизма выхода излучения от источников в астрофизике и в поисках оптимального распределения диэлектрической проницаемости, при котором происходит эффективная передача электромагнитных сигналов через слои плотной плазмы (просветление волновых барьеров).
По-существу, речь идет об эффекте резонансного туннелирования волн через структурированную среду включающую и слои непрозрачности. Иначе говоря в этом случае имеет место согласование электромагнитной волны с неоднородным диэлектрическим слоем, например, слоем плазмы.
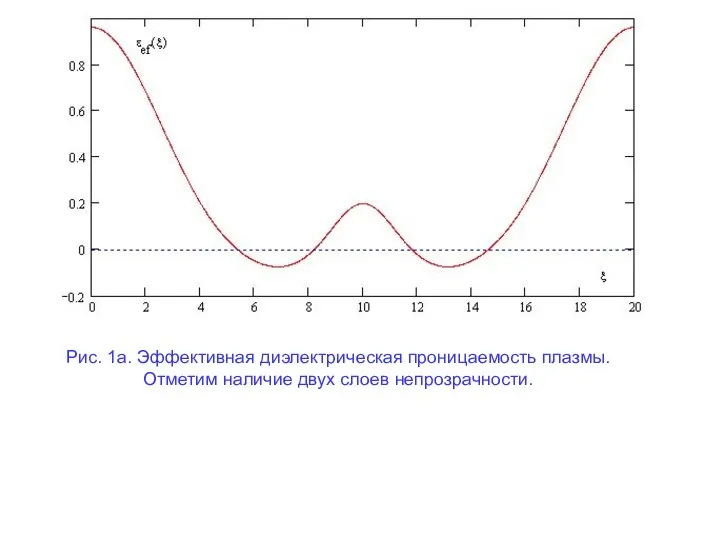
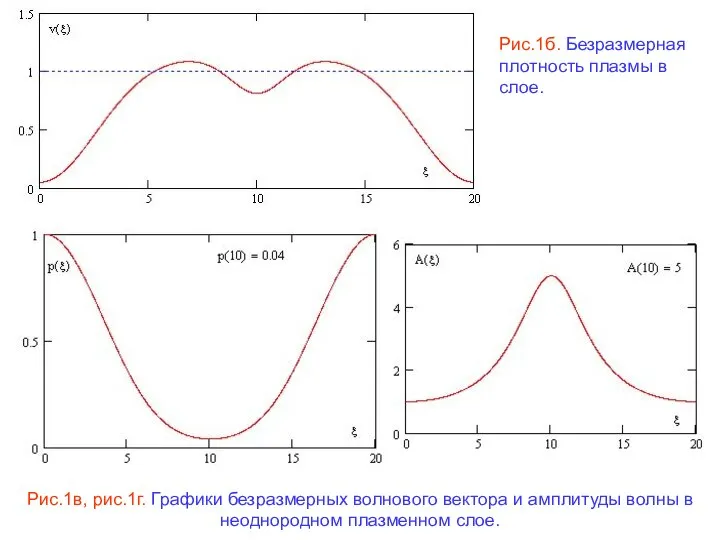
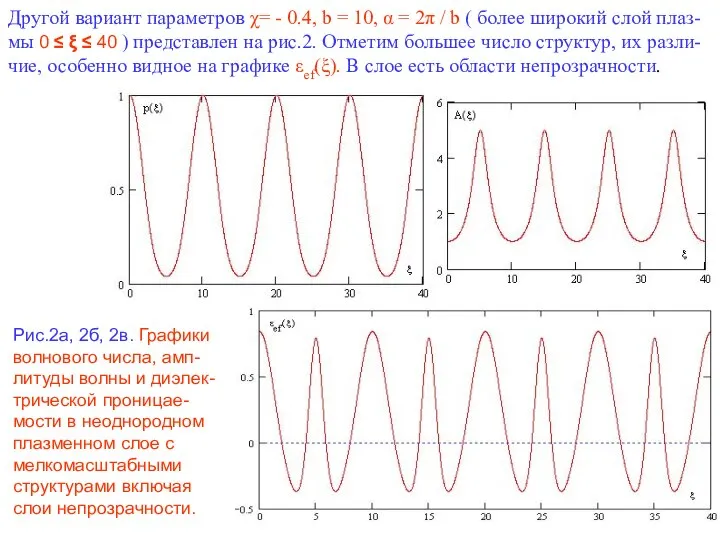
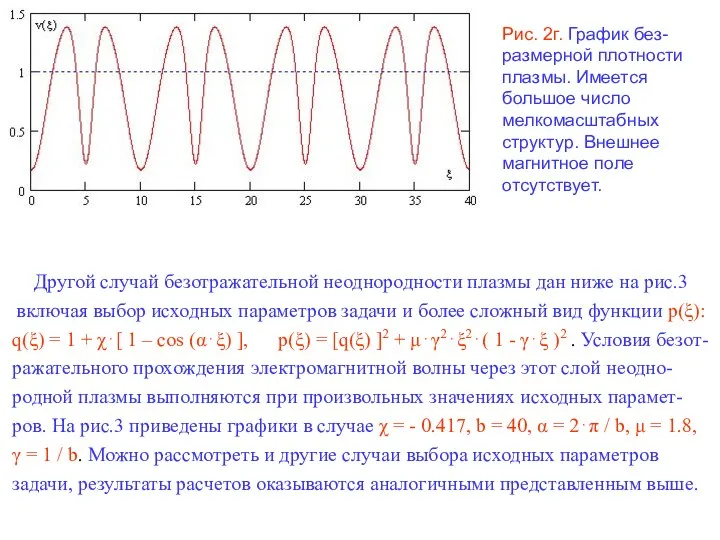
В настоящем сообщении изложены результаты исследования на основе точного линейного решения безотражательного падения электромагнитной волны на слой плазмы конечной толщины, содержащий мелкомасштабные неоднородности плотности плазмы (в масштабе вакуумной длины волны). Изучены случаи, когда диэлектрическая проницаемость как меньше, так и больше единицы (магнитоактивная плазма).
Введение






 Презентация по физике 10 класс (профильный уровень)
Презентация по физике 10 класс (профильный уровень)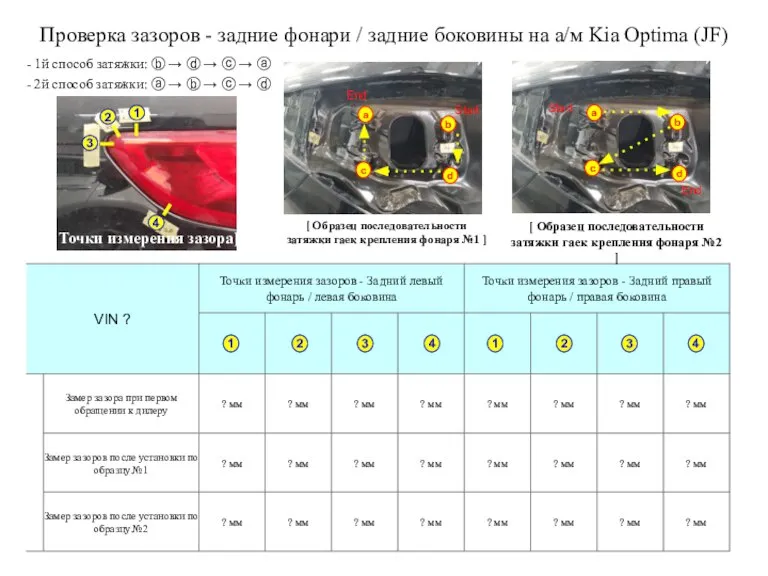 Проверка зазоров - задние фонари / задние боковины на а/м Kia Optima (JF)
Проверка зазоров - задние фонари / задние боковины на а/м Kia Optima (JF) Радиоволны. Сферы применения
Радиоволны. Сферы применения Замедляющие структуры
Замедляющие структуры Механическое оборудование для обработки мяса и рыбы. Лекция 5
Механическое оборудование для обработки мяса и рыбы. Лекция 5 Приходченко ФЕР-2032и
Приходченко ФЕР-2032и Урок 22 Відбивання світла
Урок 22 Відбивання світла Слайды по физике
Слайды по физике Инфракрасное и ультрафиолетовое излучение
Инфракрасное и ультрафиолетовое излучение Презентация на тему Светодиоды и полупроводниковые лазеры
Презентация на тему Светодиоды и полупроводниковые лазеры  Дисперсия и интерференция света Шабанова Галина Сергеевна Учитель физики КГКОУ «Вечерняя (см
Дисперсия и интерференция света Шабанова Галина Сергеевна Учитель физики КГКОУ «Вечерняя (см Тема 10. Схема устройства и принцип работы ПД
Тема 10. Схема устройства и принцип работы ПД Основные понятия теории погрешностей
Основные понятия теории погрешностей Испарение. Насыщенный и ненасыщенный пар
Испарение. Насыщенный и ненасыщенный пар Программируемые усилители
Программируемые усилители Расчёт пути и времени движения. Физика, 7 класс
Расчёт пути и времени движения. Физика, 7 класс Сила Лоренца
Сила Лоренца Радиоволны. Рудольф Генрих
Радиоволны. Рудольф Генрих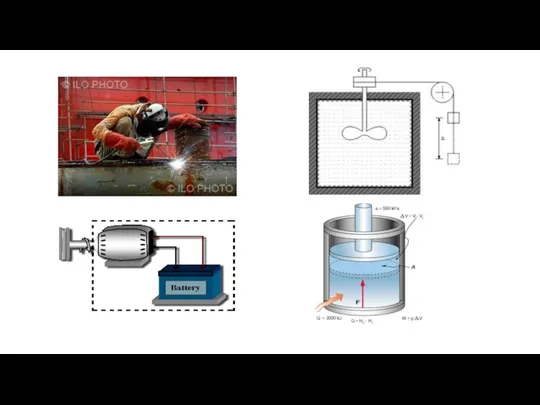 Термодинамическая работа
Термодинамическая работа Явления переноса в газах
Явления переноса в газах Оптика и механика. Физика для химиков. День пятый
Оптика и механика. Физика для химиков. День пятый Физические явления
Физические явления Полупроводниковые приборы
Полупроводниковые приборы Закон Ома для участка электрической цепи
Закон Ома для участка электрической цепи Задачи для курсовой работы
Задачи для курсовой работы Электроемкость. Электроемкость конденсатора. Энергия конденсатора
Электроемкость. Электроемкость конденсатора. Энергия конденсатора Грузовой автомобиль категории N2 с разработкой конструкции, технологии обслуживания и ремонта переднего моста
Грузовой автомобиль категории N2 с разработкой конструкции, технологии обслуживания и ремонта переднего моста Техническое обслуживание буксового узла
Техническое обслуживание буксового узла