Содержание
- 2. Курс лекций по дисциплине Механика.Теории механизмов и машин, детали машин и основы конструирования. Версия 1.0., 2005
- 3. При подготовке материала использован многолетний опыт работы автора и его коллег по совместной учёбе и работе.
- 4. Теория механизмов и машин: Учебник для втузов .К. В. Фролов, С. А. Попов, А.К. Мусатов и
- 5. 1. Иосилевич Г.Б. Детали машин. -М.: Машино- строение, 1988. - 368 с. 2. Ю.Дунаев П.Ф., Леликов
- 6. В процессе изучения курса знакомьтесь с пакетами. Для этого необходимо выйти на экран рабочего стола, выбрать
- 7. Модуль 1 Введение. Структура механизмов 1. Входной тестовый контроль к модулю1. 2. Лекции 1: 1.1. Введение.
- 8. 3. Лабораторные работы: 3.2. Структурный анализ механизмов (на моделях). 3.3. Структурирование схем механизмов в системе ДИНАМО.
- 9. Перечень вопросов входного контроля для модуля № 1: 1. Какая величина называется силой? 2. Какая величина
- 10. 9. Какое действие тел друг на друга называется механическим? 10. Что является мерой механического взаимо- действия
- 11. 16. Какая величина называется скоростью движения? 17. Какая величина называется ускорением движения? 18. Чему равна разность
- 12. 26. Что такое производная? 27. Какие свойства справедливы для производной? 28. Какая величина называется угловой скоростью?
- 13. 35. Какие стандартные масштабы являются масштабами увеличения? 36. Какие стандартные масштабы являются масштабами уменьшения? 37. Какая
- 14. 43. Что характеризует быстроту изменения углового перемещения тела с течением времени? 44. Что характеризует быстроту изменения
- 15. 48. Как называется движение, при котором точка в равные произвольно выбранные промежутки времени проходит равные пути?
- 16. 53. Как называется теорема, которой соответст- вует утверждение “Квадрат любой стороны произвольного треугольника равен сумме квадратов
- 17. 57. Что называется котангенсом острого угла прямоугольного треугольника? 58. Чему равна сумма углов в произвольном треугольнике?
- 18. ЛЕКЦИЯ № 1 1.1. Введение. Предметы и задачи дисциплины. 1.2. Элементы структуры механизмов. 1.2.1. Понятия: механизм,
- 19. 57. Что называется котангенсом острого угла прямоугольного треугольника? 58. Чему равна сумма углов в произвольном треугольнике?
- 20. Современное производство невозможно без самых разнообразных машин и механизмов.
- 21. 1.2.1. Понятия: механизм, машина Машина есть техническое устройство, предназначенное для механизации какого -либо процесса. Иногда понятия
- 22. В зависимости от выполняемых функций машины делятся на: Энергетические Технологические Транспортные Контрольные и управляющие Информационные Рис.
- 23. Типы машин Рис. 1.2 Гидравлические машины Рис. 1.3 Пневматические машины
- 24. Механизмы делятся на группы: 1. Преобразующие какую-либо энер-гию в механическую работу. Это меха-низмы энергетических машин: электро-двигатели,
- 25. 2. Потребляющие подводимую к ним энергию, выполняющие определенные технологические функции. Это механиз-мы различных станков, пищеобрабаты-вающих, полиграфических
- 26. Исполнительный механизм может работать только в том случае, если он соединён с двигателем. Двигатель и соединенный
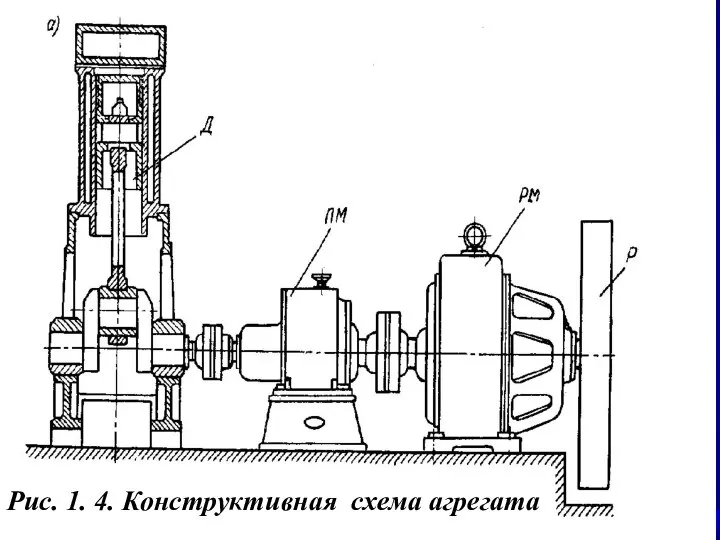
- 27. Рис. 1. 4. Конструктивная схема агрегата
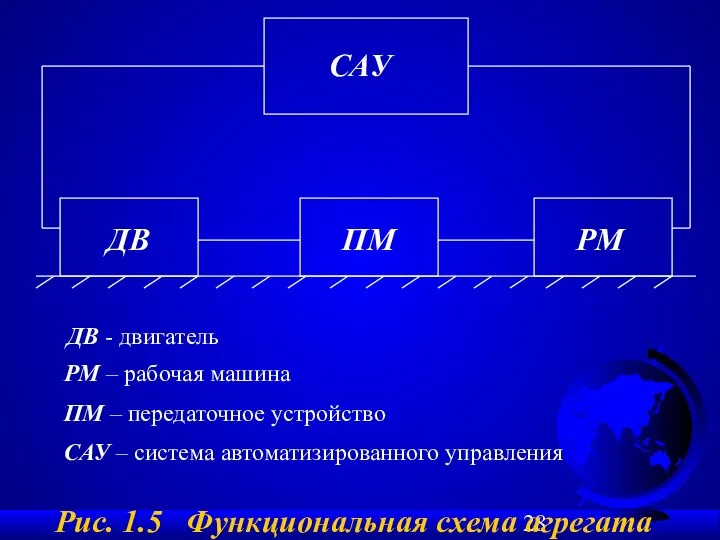
- 28. Рис. 1.5 Функциональная схема агрегата ДВ - двигатель ДВ РМ ПМ САУ РМ – рабочая машина
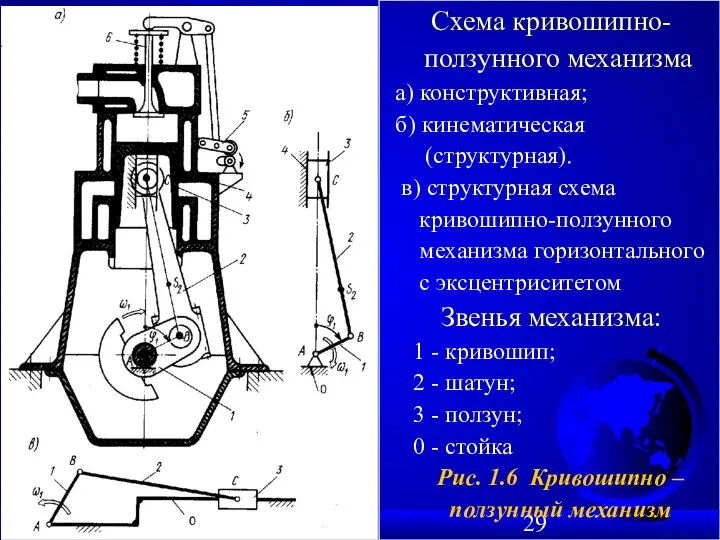
- 29. . Схема кривошипно- ползунного механизма а) конструктивная; б) кинематическая (структурная). в) структурная схема кривошипно-ползунного механизма горизонтального
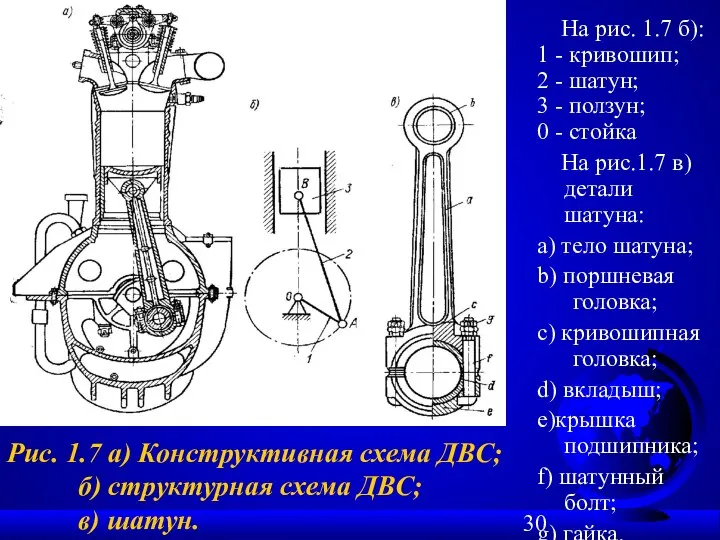
- 30. На рис. 1.7 б): 1 - кривошип; 2 - шатун; 3 - ползун; 0 - стойка
- 31. Рис. 1.8 Кривошипно-ползунный механизм (крейцкопфный) Рис. 1.9 Кривошипно-ползунный механизм (тронковый) Модели механизмов
- 32. 1.2.2. Звенья и их соединения. Кинематические пары. Механизм состоит из нескольких отдельных частей, называемых звеньями. Звено
- 33. Звено, которое определяет движение других звеньев называется входным звеном (ведущим). Движение входному звену задается извне. Чаще
- 34. Особое место занимают механизмы, в кото-рых имеются промежуточные (вспомогательные) звенья. Они могут быть твёрдыми (ролики, шари-ки),
- 35. Свободное материальное тело в пространстве имеет 6 возможных независимых движений (три поступательных вдоль координатных осей x,
- 36. В механизме все звенья связаны друг с другом. Связь может быть геометрической и динамической. Связь геометрическая,
- 37. Звенья в механизме связаны друг с другом, следовательно они теряют подвижность. Каждое соединение ограничивает движение звеньев.
- 38. Кинематические пары классифицируются либо по числу наложенных условий связи, либо по числу оставшихся движений. В нашем
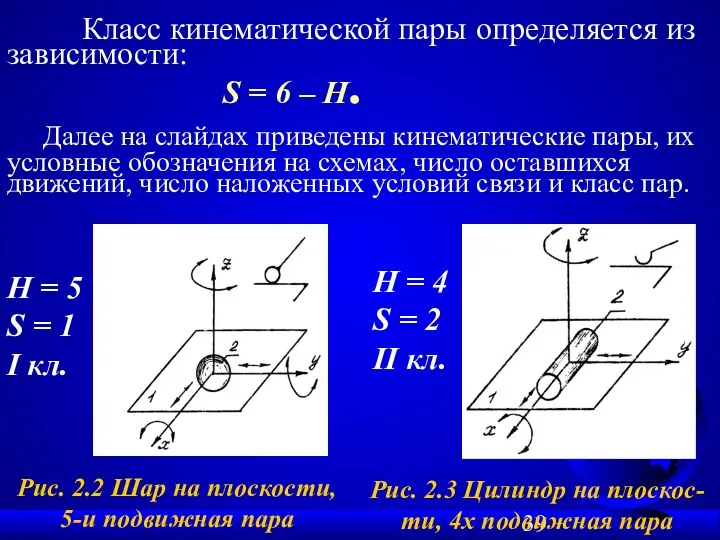
- 39. Класс кинематической пары определяется из зависимости: S = 6 – H. Далее на слайдах приведены кинематические
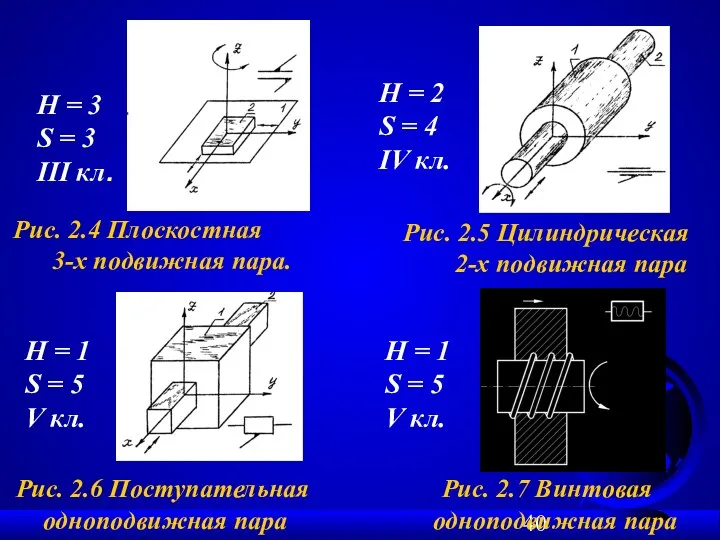
- 40. H = 3 S = 3 III кл. H = 2 S = 4 IV кл.
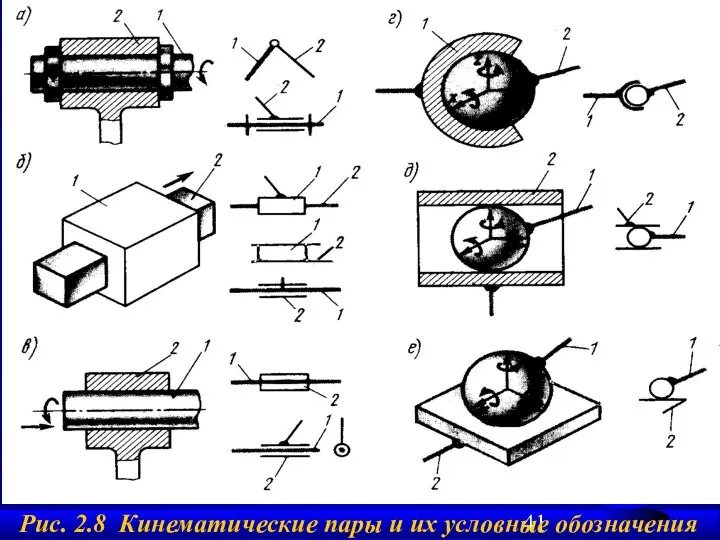
- 41. Рис. 2.8 Кинематические пары и их условные обозначения
- 42. Эта мультипликация сделана студентом специаль-ности ЭПОПТ и ТТ Куликом Евгением в 2000 году.
- 43. Эта мультипликация сделана студентом специаль-ности ЭПОПТ и ТТ Куликом Евгением в 2000 году.
- 44. Эта мультипликация сделана студентом специаль-ности ЭПОПТ и ТТ Куликом Евгением в 2000 году.
- 45. Эта мультипликация сделана студентом специаль-ности ЭПОПТ и ТТ Куликом Евгением в 2000 году.
- 46. Эта мультипликация сделана студентом специаль-ности ЭПОПТ и ТТ Куликом Евгением в 2000 году.
- 47. Эта мультипликация сделана студентом специаль-ности ЭПОПТ и ТТ Куликом Евгением в 2000 году.
- 48. Эта мультипликация сделана студентом специаль-ности ЭПОПТ и ТТ Куликом Евгением в 2000 году.
- 49. Эта мультипликация сделана студентом специаль-ности ЭПОПТ и ТТ Куликом Евгением в 2000 году.
- 50. Эта мультипликация сделана студентом специаль-ности ЭПОПТ и ТТ Куликом Евгением в 2000 году.
- 51. Эта мультипликация сделана студентом специаль-ности ЭПОПТ и ТТ Куликом Евгением в 2000 году.
- 52. Эта мультипликация сделана студентом специаль-ности ЭПОПТ и ТТ Куликом Евгением в 2000 году.
- 53. Эта мультипликация сделана студентом специаль-ности ЭПОПТ и ТТ Куликом Евгением в 2000 году.
- 54. Эта мультипликация сделана студентом специаль-ности ЭПОПТ и ТТ Куликом Евгением в 2000 году.
- 55. Эта мультипликация сделана студентом специаль-ности ЭПОПТ и ТТ Куликом Евгением в 2000 году.
- 56. Эта мультипликация сделана студентом специаль-ности ЭПОПТ и ТТ Куликом Евгением в 2000 году.
- 57. Эта мультипликация сделана студентом специаль-ности ЭПОПТ и ТТ Куликом Евгением в 2000 году.
- 58. Эта мультипликация сделана студентом специаль-ности ЭПОПТ и ТТ Куликом Евгением в 2000 году.
- 59. Эта мультипликация сделана студентом специаль-ности ЭПОПТ и ТТ Куликом Евгением в 2000 году.
- 60. Эта мультипликация сделана студентом специаль-ности ЭПОПТ и ТТ Куликом Евгением в 2000 году.
- 61. Эта мультипликация сделана студентом специаль-ности ЭПОПТ и ТТ Куликом Евгением в 2000 году.
- 62. Эта мультипликация сделана студентом специаль-ности ЭПОПТ и ТТ Куликом Евгением в 2000 году.
- 63. Эта мультипликация сделана студентом специаль-ности ЭПОПТ и ТТ Куликом Евгением в 2000 году.
- 64. Эта мультипликация сделана студентом специаль-ности ЭПОПТ и ТТ Куликом Евгением в 2000 году.
- 65. Эта мультипликация сделана студентом специаль-ности ЭПОПТ и ТТ Куликом Евгением в 2000 году.
- 66. Рис. 2.9 Высшая пара в кулачковых механизмах Рис. 2.10 Высшая пара в зубчатых механизмах Поверхности, линии,
- 67. Рис. 2.11 Силовое замыкание высшей пары Рис. 2.12 Геометрическое замыкание высшей пар Кинематические пары могут быть
- 68. 1. 2.3. Степень подвижности механизма Шесть степеней свободы несвязанного твёрдого тела соответствует шести независимым координатам, опреде-ляющим
- 69. В основе любого механизма лежит кинематическая цепь. Это совокупность звеньев, соединённых кинемати-ческими парами. Сложные цепи -
- 70. Сумма всех условий связи, наложенных всеми кинема-тическими парами в общем случае: Степень свободы кинематической цепи зависит
- 71. В механизмах движение рассматривается относительно какого-то звена (стойки), поэтому сразу исключается 6 степеней свободы стойки. n
- 72. Эта формула справедлива, если не наложено никаких других общих дополнительных условий. Условия могут быть самыми разными.
- 73. В плоских механизмах все звенья должны двигаться в одной плоскости или в параллельных плоскостях, т. е.
- 74. Пример 1. Для механизма, изображённого на рис. 2.16.: Рис. 2.16 Пространственный кривошипно-ползунный механизм Рассмотрим примеры: i=1.
- 75. Рис. 2.17 Плоский кривошипно- ползунный механизм Пример 2. Для механизма, изображённого на рис. 2. 17: Входные
- 76. 1. 2.4. Структурный синтез и анализ механизмов. минимальное число звеньев в механизме должно быть 3. Такой
- 77. Входное (начальное) звено со стойкой прини-мается за некоторый условный механизм, который называют исходным механизмом. В плоских
- 78. Если к исходному механизму присоединить некоторые структурные группы с W = 0, то мож-но получить различные
- 79. Таблица 3. 1. Особенности группы Ассура: 1. Число звеньев в группе четное. 2. Стойка не входит
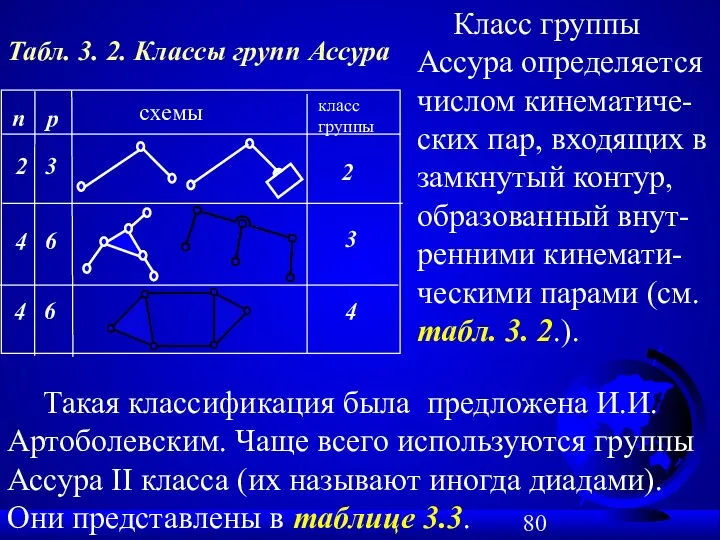
- 80. Табл. 3. 2. Классы групп Ассура Класс группы Ассура определяется числом кинематиче-ских пар, входящих в замкнутый
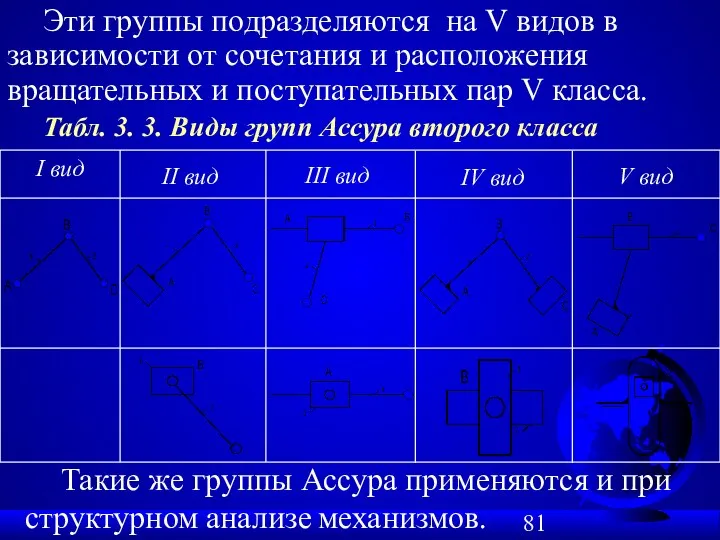
- 81. Эти группы подразделяются на V видов в зависимости от сочетания и расположения вращательных и поступательных пар
- 82. Первый вид - все три пары вращательные. Второй вид - две пары вращательные, одна (внешняя) поступательная.
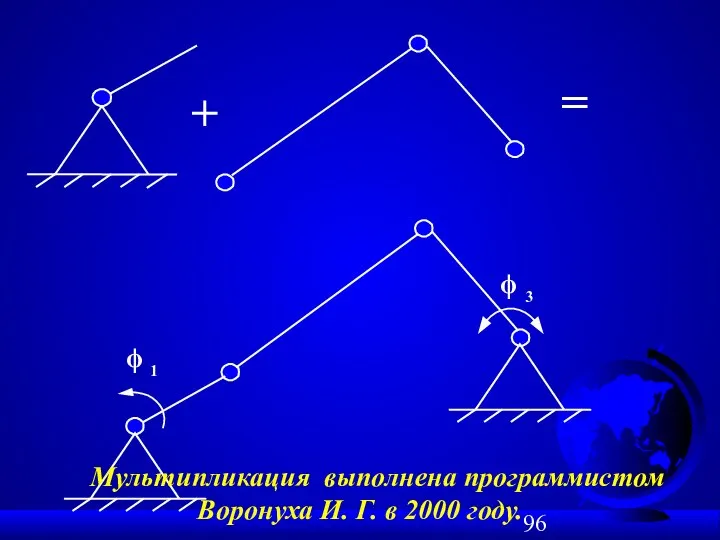
- 83. Как построить схему механизма? Пример № 1 структурного синтеза плоских механизмов: W = 1; n =
- 84. Мультипликация выполнена программистом Воронуха И. Г. в 2000 году.
- 85. Мультипликация выполнена программистом Воронуха И. Г. в 2000 году.
- 86. Мультипликация выполнена программистом Воронуха И. Г. в 2000 году.
- 87. Мультипликация выполнена программистом Воронуха И. Г. в 2000 году.
- 88. Мультипликация выполнена программистом Воронуха И. Г. в 2000 году.
- 89. Мультипликация выполнена программистом Воронуха И. Г. в 2000 году.
- 90. Мультипликация выполнена программистом Воронуха И. Г. в 2000 году.
- 91. Мультипликация выполнена программистом Воронуха И. Г. в 2000 году.
- 92. Мультипликация выполнена программистом Воронуха И. Г. в 2000 году.
- 93. Мультипликация выполнена программистом Воронуха И. Г. в 2000 году.
- 94. Мультипликация выполнена программистом Воронуха И. Г. в 2000 году.
- 95. Мультипликация выполнена программистом Воронуха И. Г. в 2000 году.
- 96. + = ϕ 1 ϕ 3 Мультипликация выполнена программистом Воронуха И. Г. в 2000 году.
- 97. Мультипликация выполнена программистом Воронуха И. Г. в 2000 году.
- 98. Мультипликация выполнена программистом Воронуха И. Г. в 2000 году.
- 99. Мультипликация выполнена программистом Воронуха И. Г. в 2000 году.
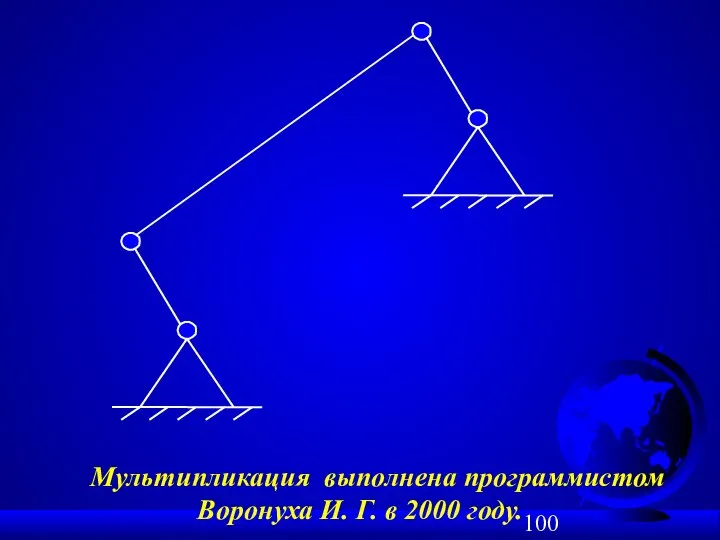
- 100. Мультипликация выполнена программистом Воронуха И. Г. в 2000 году.
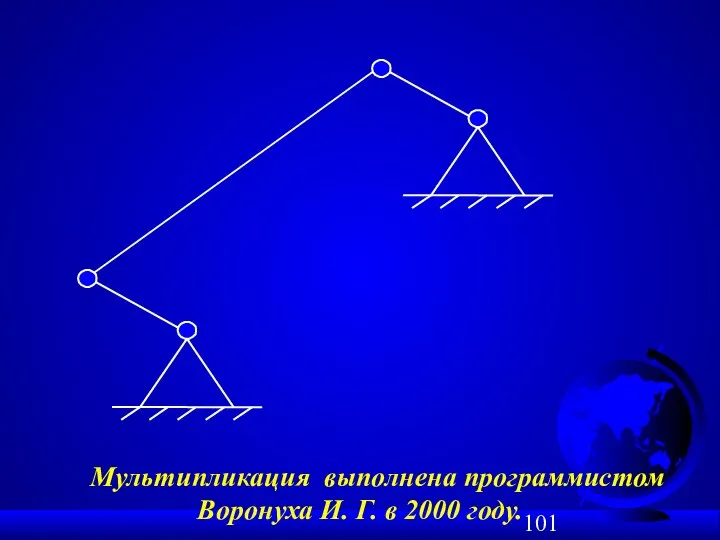
- 101. Мультипликация выполнена программистом Воронуха И. Г. в 2000 году.
- 102. Мультипликация выполнена программистом Воронуха И. Г. в 2000 году.
- 103. Мультипликация выполнена программистом Воронуха И. Г. в 2000 году.
- 104. Мультипликация выполнена программистом Воронуха И. Г. в 2000 году.
- 105. Мультипликация выполнена программистом Воронуха И. Г. в 2000 году.
- 106. Мультипликация выполнена программистом Воронуха И. Г. в 2000 году.
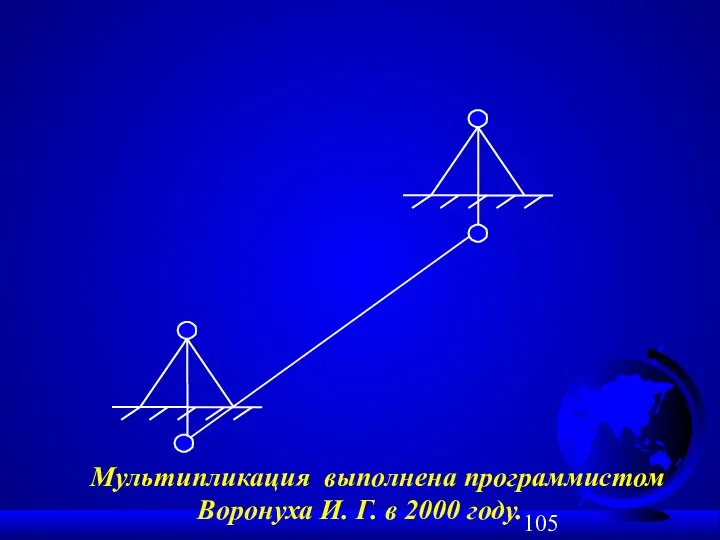
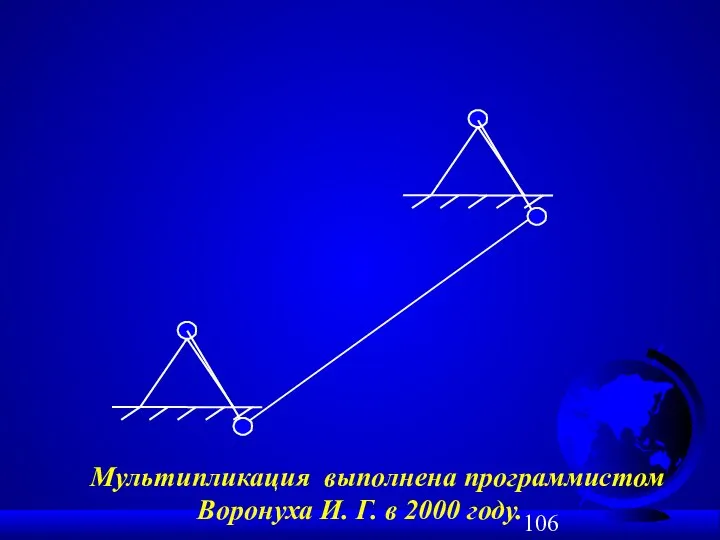
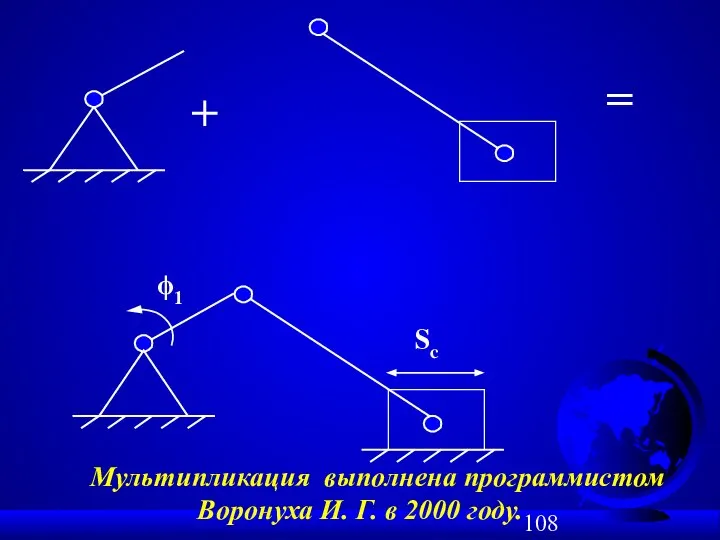
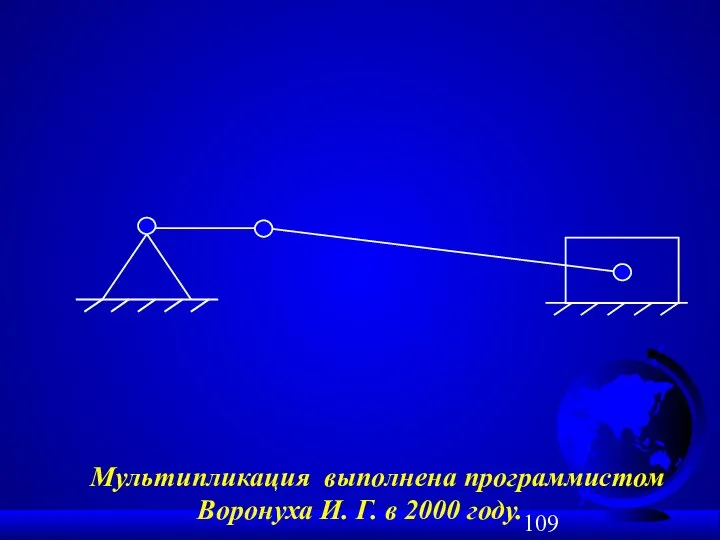
- 107. Пример № 2 структурного синтеза плоских механизмов: W = 1; n = 3; p5 = 4.
- 108. + = ϕ1 Sc Мультипликация выполнена программистом Воронуха И. Г. в 2000 году.
- 109. Мультипликация выполнена программистом Воронуха И. Г. в 2000 году.
- 110. Мультипликация выполнена программистом Воронуха И. Г. в 2000 году.
- 111. Мультипликация выполнена программистом Воронуха И. Г. в 2000 году.
- 112. Мультипликация выполнена программистом Воронуха И. Г. в 2000 году.
- 113. Мультипликация выполнена программистом Воронуха И. Г. в 2000 году.
- 114. Мультипликация выполнена программистом Воронуха И. Г. в 2000 году.
- 115. Мультипликация выполнена программистом Воронуха И. Г. в 2000 году.
- 116. Мультипликация выполнена программистом Воронуха И. Г. в 2000 году.
- 117. Мультипликация выполнена программистом Воронуха И. Г. в 2000 году.
- 118. Мультипликация выполнена программистом Воронуха И. Г. в 2000 году.
- 119. Мультипликация выполнена программистом Воронуха И. Г. в 2000 году.
- 120. Мультипликация выполнена программистом Воронуха И. Г. в 2000 году.
- 121. Мультипликация выполнена программистом Воронуха И. Г. в 2000 году.
- 122. + = Пример № 3 структурного синтеза плоских механизмов: W = 2; n = 4; p5
- 123. W = 1; n = 5; p5 = 7. + = + Пример № 4 структурного
- 124. Таким образом выполняется структурный синтез механизмов. В системе ДИНАМО используются обобщённые структурные модули, позволяющие структурировать схемы
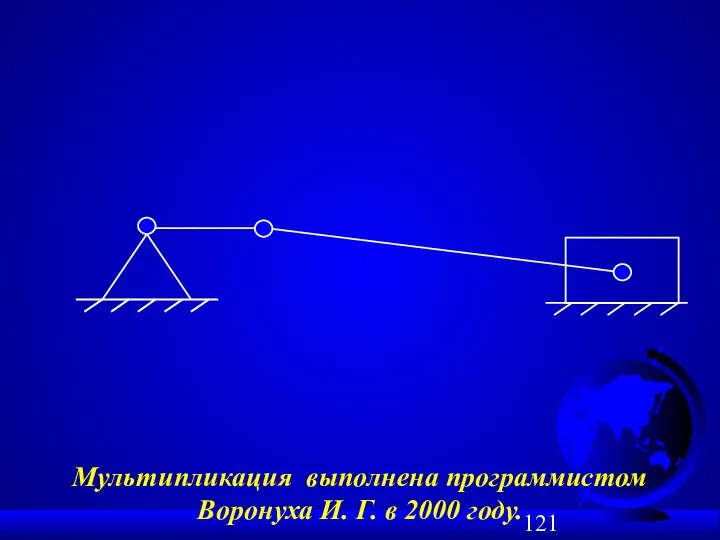
- 125. Структурный анализ механизма - это процедура, обратная структурному синтезу. Выполняется путем расчленения его на структурные группы
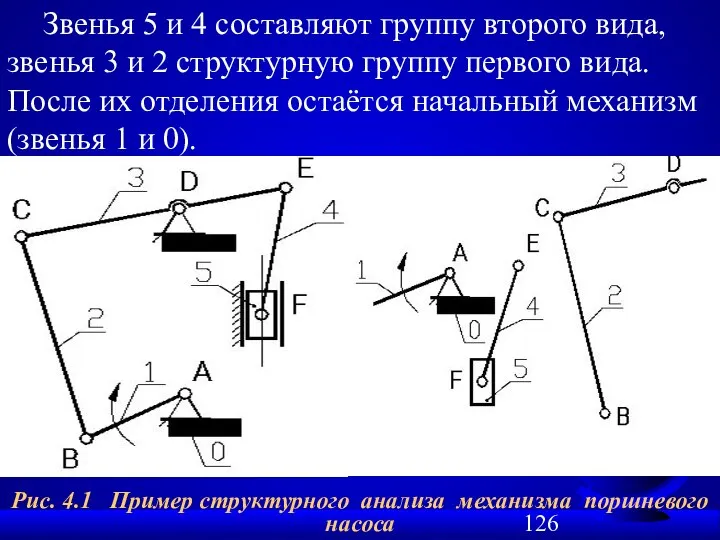
- 126. Рис. 4.1 Пример структурного анализа механизма поршневого насоса Звенья 5 и 4 составляют группу второго вида,
- 127. При выделении групп из механизма условно считается, что кинематические пары, соединяющие звенья с начальным механизмом, отходят
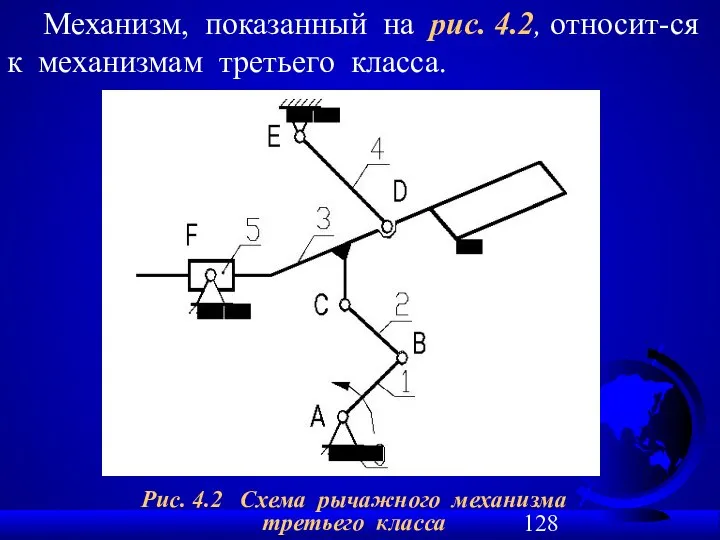
- 128. Рис. 4.2 Схема рычажного механизма третьего класса Механизм, показанный на рис. 4.2, относит-ся к механизмам третьего
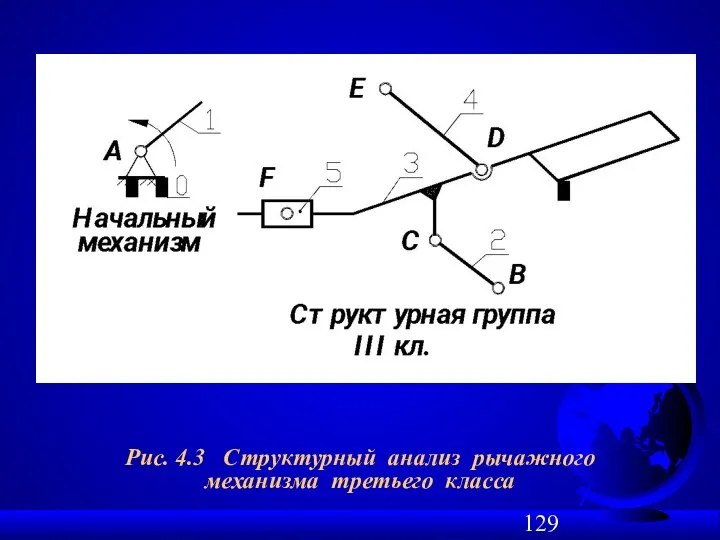
- 129. Рис. 4.3 Структурный анализ рычажного механизма третьего класса
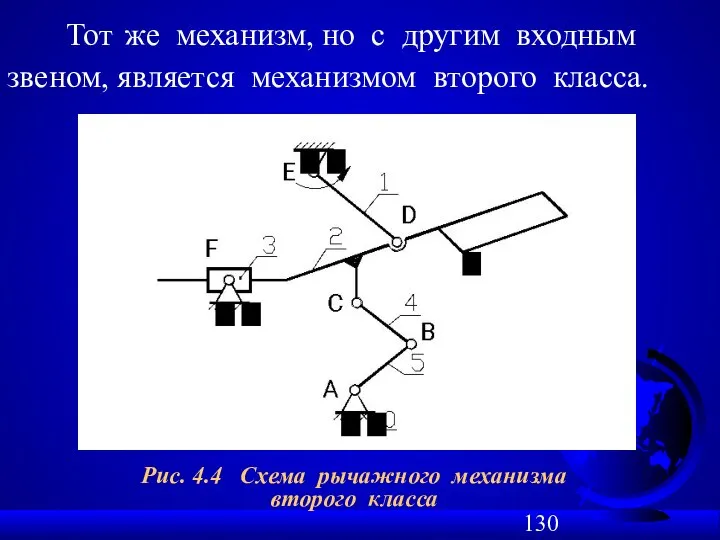
- 130. Рис. 4.4 Схема рычажного механизма второго класса Тот же механизм, но с другим входным звеном, является
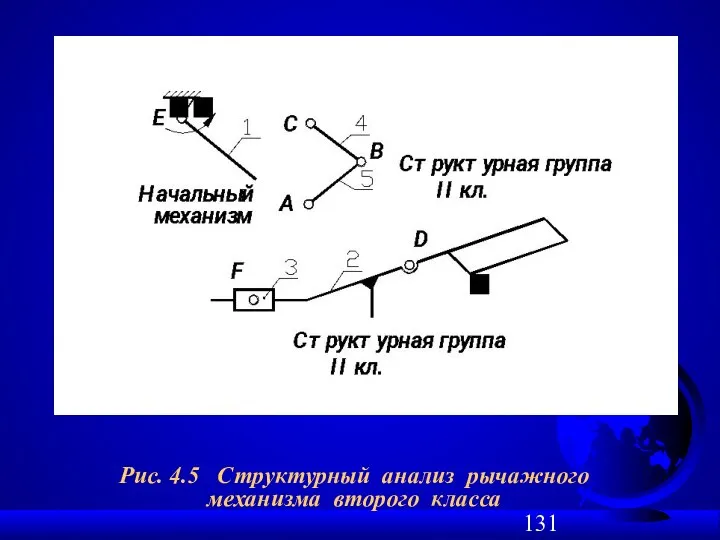
- 131. Рис. 4.5 Структурный анализ рычажного механизма второго класса
- 132. Для механизма, показанного на рис. 4.2, формула строения имеет вид: Строение механизма можно записать услов-ной формулой.
- 133. Порядок структурного анализа 1. Пронумеровать звенья арабскими цифрами, входное звено обозначив цифрой 1, стойку - цифрой
- 134. 7. Выделить начальные механизмы. 8. Оставшуюся кинематическую цепь разложить на структурные группы. 9. Определить класс, порядок
- 135. Детали машин ─ основы расчета и конструирования деталей машин По условиям производства и монтажа части механизмов
- 136. Деталь ─ изделие, изготовленное из однородного по наименованию и марке материала, без применения сборочных операций; Сборочная
- 137. Различают детали машин общего и специального назначения к деталям машин общего назначения относятся: 1. детали и
- 138. 3. Детали и узлы для осуществления вращательного и поступательного движения частей машин: оси и валы, подшипник
- 139. Являясь частями самых различных машин, детали машин общего назначения выполняют в них одинаковые функции. Поэтому, весьма
- 140. Предмет ТММ тесно связан с основными теоретическими дисцип-линами: математикой, физикой, теоретической механикой. Вместе с курсами сопротивления
- 142. Скачать презентацию













































































































 Механічна робота, потужність
Механічна робота, потужність Равномерное движение по окружности
Равномерное движение по окружности Механическая работа
Механическая работа Izolace, separace a detekce proteinů část ii
Izolace, separace a detekce proteinů část ii Радиация. Радиоактивный распад
Радиация. Радиоактивный распад Общие принципы управления и особенности осуществления
Общие принципы управления и особенности осуществления ОГЭ-2022 по физике. Задания, требования и изменения в сравнении с ОГЭ-2020
ОГЭ-2022 по физике. Задания, требования и изменения в сравнении с ОГЭ-2020 Взаимодействие проводников с током
Взаимодействие проводников с током Электромагнитные волны
Электромагнитные волны Изобретение радио
Изобретение радио Количество теплоты
Количество теплоты Абразивная резка
Абразивная резка Электрический ток в жидкостях
Электрический ток в жидкостях Взаимосвязь электрического сопротивления графита с его положением в пространстве
Взаимосвязь электрического сопротивления графита с его положением в пространстве Архимедова сила. 7 класс
Архимедова сила. 7 класс Закон сохранения энергии
Закон сохранения энергии Презентация на тему Связь в России
Презентация на тему Связь в России  Закон Ома для участка цепи
Закон Ома для участка цепи Электрический ток. Источники тока
Электрический ток. Источники тока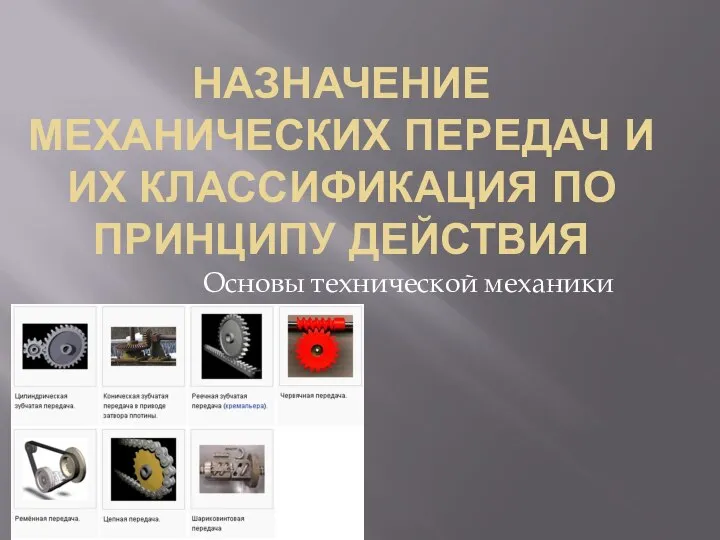 Назначение механических передач и их классификация по принципу действия
Назначение механических передач и их классификация по принципу действия Ядерный реактор. Ядерная энергетика. Экологические проблемы работы атомных электростанций
Ядерный реактор. Ядерная энергетика. Экологические проблемы работы атомных электростанций Принцип работы профилемеров
Принцип работы профилемеров Силовое действие магнитного поля
Силовое действие магнитного поля Равенство работ при использовании простых механизмов. Золотое правило механики
Равенство работ при использовании простых механизмов. Золотое правило механики Урал детям. Проект школы №734
Урал детям. Проект школы №734 Магнитное поле. Магнитное поле прямого тока. Магнитные линии
Магнитное поле. Магнитное поле прямого тока. Магнитные линии Инжекторный двигатель Автор Skyfury Sparkle
Инжекторный двигатель Автор Skyfury Sparkle Рентгеновские лучи
Рентгеновские лучи