Метод переходного состояния. Классическая теория

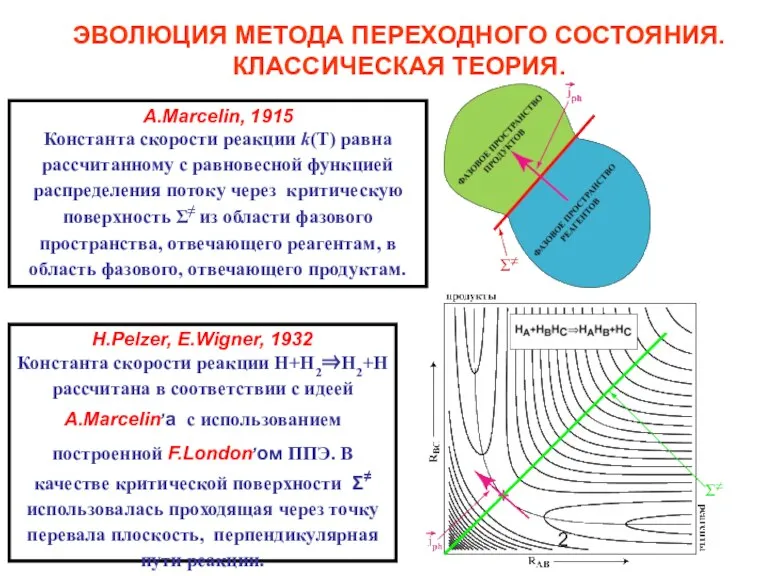
ЭВОЛЮЦИЯ МЕТОДА ПЕРЕХОДНОГО СОСТОЯНИЯ.
КЛАССИЧЕСКАЯ ТЕОРИЯ.
A.Marcelin, 1915
Константа скорости реакции k(T) равна рассчитанному с равновесной функцией распределения потоку через критическую поверхность Σ≠ из области фазового пространства, отвечающего реагентам, в область фазового, отвечающего продуктам.
H.Pelzer, E.Wigner, 1932
Константа скорости реакции H+H2⇒H2+H рассчитана в соответствии с идеей A.Marcelin,а с использованием построенной F.London,ом ППЭ. В качестве критической поверхности Σ≠ использовалась проходящая через точку перевала плоскость, перпендикулярная пути реакции.

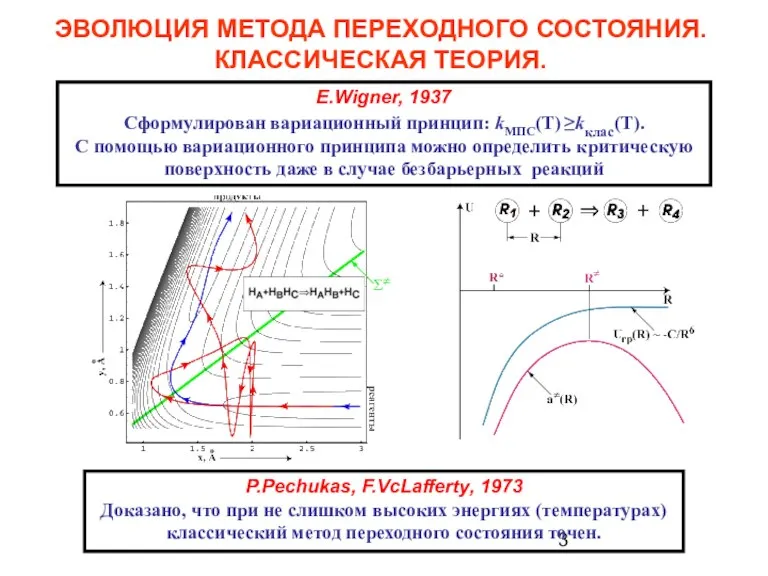
ЭВОЛЮЦИЯ МЕТОДА ПЕРЕХОДНОГО СОСТОЯНИЯ.
КЛАССИЧЕСКАЯ ТЕОРИЯ.
E.Wigner, 1937
Сформулирован вариационный принцип: kМПС(T) ≥kклас(T).
С помощью вариационного принципа можно определить критическую поверхность даже в случае безбарьерных реакций
P.Pechukas, F.VcLafferty, 1973
Доказано, что при не слишком высоких энергиях (температурах) классический метод переходного состояния точен.

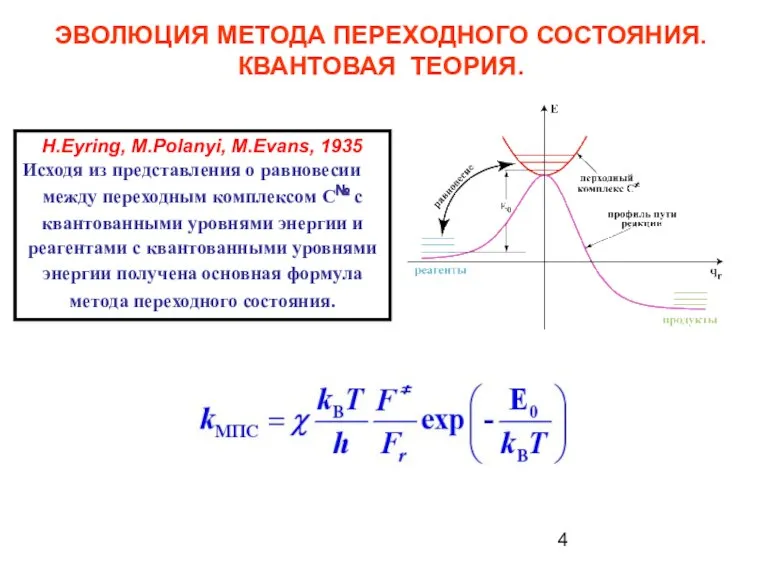
ЭВОЛЮЦИЯ МЕТОДА ПЕРЕХОДНОГО СОСТОЯНИЯ.
КВАНТОВАЯ ТЕОРИЯ.
H.Eyring, M.Polanyi, M.Evans, 1935
Исходя из представления о равновесии
между переходным комплексом C№ с
квантованными уровнями энергии и
реагентами с квантованными уровнями
энергии получена основная формула
метода переходного состояния.

МЕТОД ПЕРЕХОДНОГО СОСТОЯНИЯ
ЭЙРИНГА-ПОЛЯНИ-ЭВАНСА.
ОЦЕНКА ПРЕДЭКСПОНЕНТА ДЛЯ ПРЯМЫХ БИМОЛЕКУЛЯРНЫХ РЕАКЦИЙ.
Из общей формулы метода переходного состояния следует, что предэкспонент растет с увеличением числа вращательных степеней свободы переходного комплекса и падает с увеличением числа вращательных степеней свободы реагентов.

МЕТОД ПЕРЕХОДНОГО СОСТОЯНИЯ
ЭЙРИНГА-ПОЛЯНИ-ЭВАНСА.
ТЕРМОДИНАМИЧЕСКАЯ ФОРМУЛИРОВКА.
H.Eyring, M.Polanyi, M.Evans, 1935
Основная формула метода переходного состояния переписывается в виде произведения частотного фактора и константы равновесия между переходным комплексом и реагентами.
S.Benson, 1958
«Химические силы» короткодействующие. Поэтому термодинамические свойства характерных химических групп мало меняются при переносе из одной молекулы (переходного комплекса) в другую (другой).

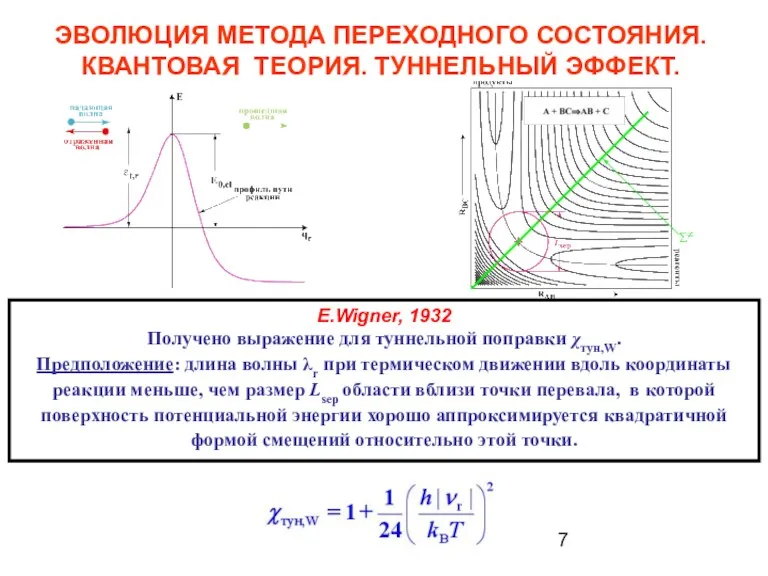
ЭВОЛЮЦИЯ МЕТОДА ПЕРЕХОДНОГО СОСТОЯНИЯ.
КВАНТОВАЯ ТЕОРИЯ. ТУННЕЛЬНЫЙ ЭФФЕКТ.
E.Wigner, 1932
Получено выражение для туннельной поправки χтун,W.
Предположение: длина волны λr при термическом движении вдоль координаты реакции меньше, чем размер Lsep области вблизи точки перевала, в которой поверхность потенциальной энергии хорошо аппроксимируется квадратичной формой смещений относительно этой точки.

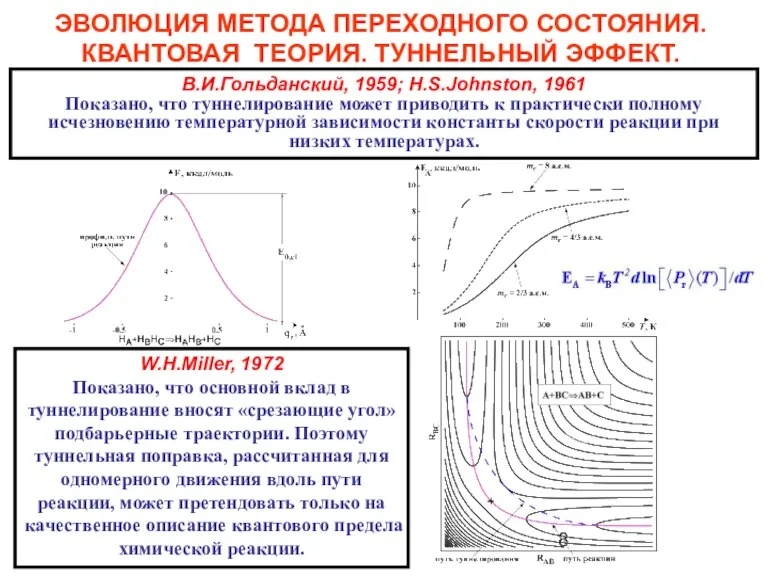
ЭВОЛЮЦИЯ МЕТОДА ПЕРЕХОДНОГО СОСТОЯНИЯ.
КВАНТОВАЯ ТЕОРИЯ. ТУННЕЛЬНЫЙ ЭФФЕКТ.
В.И.Гольданский, 1959; H.S.Johnston, 1961
Показано, что туннелирование может приводить к практически полному исчезновению температурной зависимости константы скорости реакции при низких температурах.
W.H.Miller, 1972
Показано, что основной вклад в туннелирование вносят «срезающие угол» подбарьерные траектории. Поэтому туннельная поправка, рассчитанная для одномерного движения вдоль пути реакции, может претендовать только на качественное описание квантового предела химической реакции.

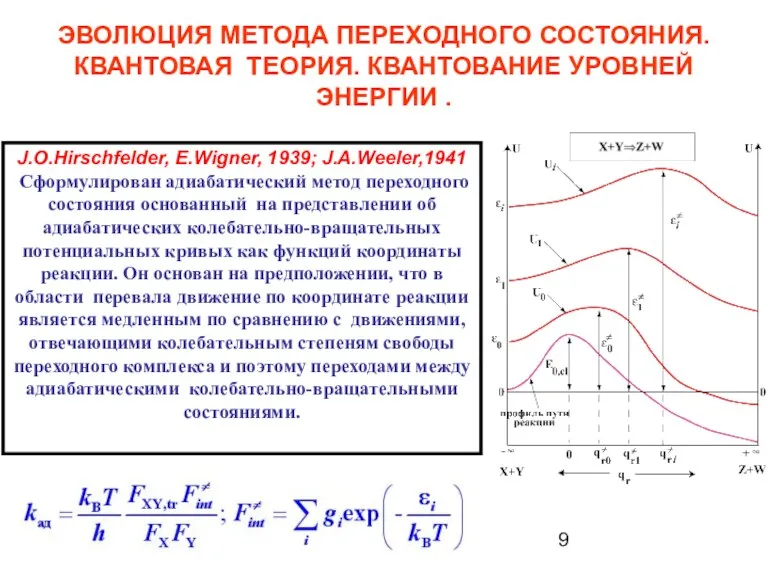
ЭВОЛЮЦИЯ МЕТОДА ПЕРЕХОДНОГО СОСТОЯНИЯ.
КВАНТОВАЯ ТЕОРИЯ. КВАНТОВАНИЕ УРОВНЕЙ ЭНЕРГИИ .
J.O.Hirschfelder, E.Wigner, 1939; J.A.Weeler,1941 Сформулирован адиабатический метод переходного состояния основанный на представлении об адиабатических колебательно-вращательных потенциальных кривых как функций координаты реакции. Он основан на предположении, что в области перевала движение по координате реакции является медленным по сравнению с движениями, отвечающими колебательным степеням свободы переходного комплекса и поэтому переходами между
адиабатическими колебательно-вращательными состояниями.

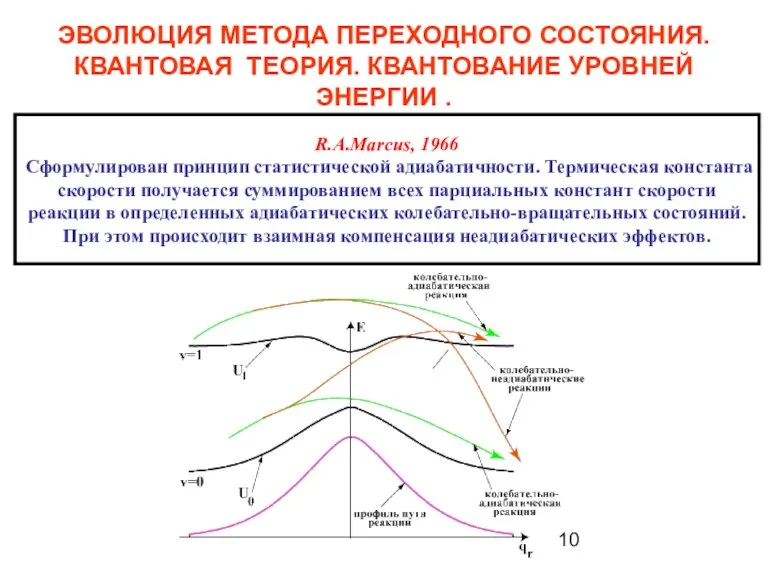
ЭВОЛЮЦИЯ МЕТОДА ПЕРЕХОДНОГО СОСТОЯНИЯ.
КВАНТОВАЯ ТЕОРИЯ. КВАНТОВАНИЕ УРОВНЕЙ ЭНЕРГИИ .
R.A.Marcus, 1966
Сформулирован принцип статистической адиабатичности. Термическая константа скорости получается суммированием всех парциальных констант скорости реакции в определенных адиабатических колебательно-вращательных состояний. При этом происходит взаимная компенсация неадиабатических эффектов.

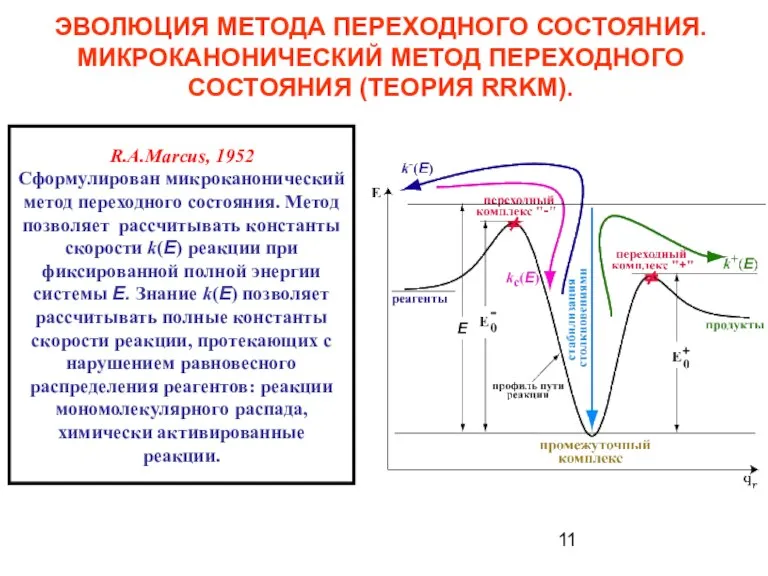
ЭВОЛЮЦИЯ МЕТОДА ПЕРЕХОДНОГО СОСТОЯНИЯ.
МИКРОКАНОНИЧЕСКИЙ МЕТОД ПЕРЕХОДНОГО СОСТОЯНИЯ (ТЕОРИЯ RRKM).
R.A.Marcus, 1952
Сформулирован микроканонический метод переходного состояния. Метод позволяет рассчитывать константы скорости k(E) реакции при фиксированной полной энергии системы E. Знание k(E) позволяет рассчитывать полные константы скорости реакции, протекающих с нарушением равновесного распределения реагентов: реакции мономолекулярного распада, химически активированные реакции.

СОВРЕМЕННЫЙ СТАТУС МЕТОДА ПЕРЕХОДНОГО СОСТОЯНИЯ.
Классический метод переходного состояния представляет из себя строгую теорию в случае, если «долины» реагентов и продуктов разделены единственным перевалом. Качество приближенных расчетов констант скорости можно последовательно улучшать с использованием вариационного принципа.
Если вигнеровская поправка на туннелирование меньше двух, квантовые поправки к термической константе скорости могут быть учтены в рамках стандартной теории Эйринга-Поляни-Эванса.
В этих условиях микроканонический метод переходного состояния (теория RRKM) позволяет рассчитывать константы скорости в условиях нарушения больцмановского распределения.
Учет больших туннельных эффектов требует выхода за рамки метода переходного состояния в том смысле, что требуется анализ динамики в такой окрестности перевала, где уже нельзя отделить движение по координате реакции от остальных движений.
Метод переходного состояния неприменим для расчета констант скорости реакций из определенных квантовых состояний реагентов в определенные квантовые состояния продуктов.