Слайд 2Для того, чтобы учесть релаксацию напряжений у вершины трещины, вводятся модели с
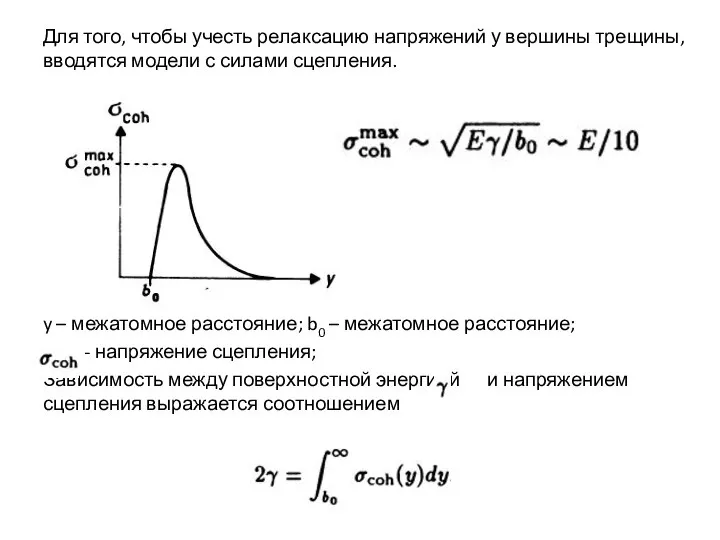
силами сцепления.
y – межатомное расстояние; b0 – межатомное расстояние;
– - напряжение сцепления;
Зависимость между поверхностной энергией и напряжением сцепления выражается соотношением
Слайд 3
Основные гипотезы концепции сил сцепления:
1) Длина зоны действия сил сцепления мала
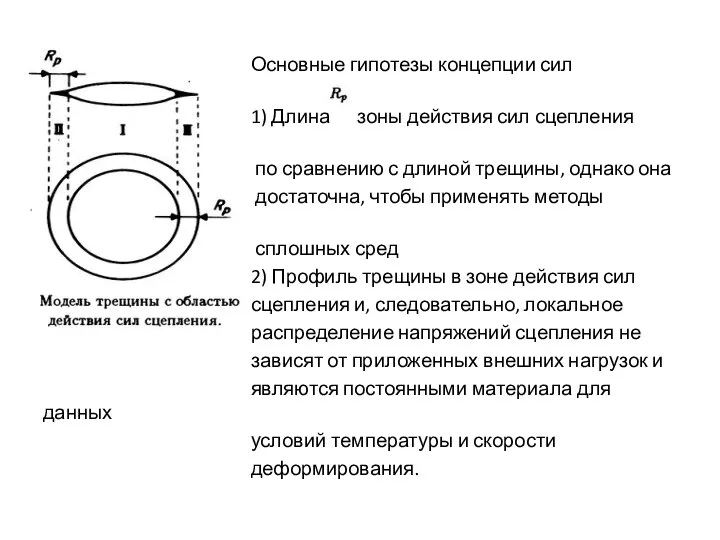
по сравнению с длиной трещины, однако она
достаточна, чтобы применять методы механики
сплошных сред
2) Профиль трещины в зоне действия сил
сцепления и, следовательно, локальное
распределение напряжений сцепления не
зависят от приложенных внешних нагрузок и
являются постоянными материала для данных
условий температуры и скорости
деформирования.
Слайд 4Поля напряжений и перемещений можно представить в виде двух составляющих:
поля, соответствующие телу

без трещины, на которое действует заданная внешняя нагрузка;
поля, соответствующие телу с трещиной, на берегах которой действуют напряжения , представляющие собой разность между напряжениями сцепления и приложенными внешними напряжениями.
Коэффициент интенсивности напряжений подобной модели можно получить, используя принцип наложения:
где - коэффициент интенсивности напряжений, связанный с внешней нагрузкой; - коэффициент интенсивности напряжений, связанный с силами сцепления
Слайд 5Модель Дагдейла.
Модель Дагдейла представляет действительную трещину длиной , от вершины которой физически
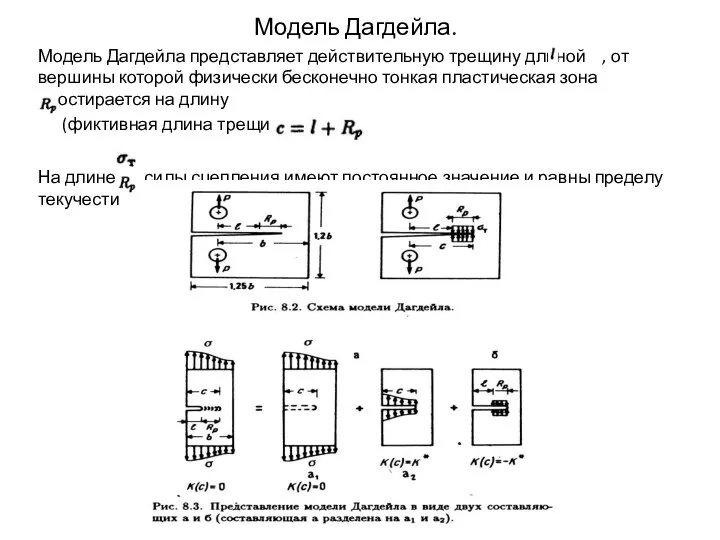
бесконечно тонкая пластическая зона простирается на длину
(фиктивная длина трещины).
На длине силы сцепления имеют постоянное значение и равны пределу текучести .
Слайд 6Коэффициент интенсивности напряжений в случае «а» равен:
Коэффициент интенсивности напряжений в случае «б»

составляет:
Требование, чтобы перемещения были равны нулю в вершине трещины длиной с, определяется соотношением
Это условие приводит к соотношению
откуда . Размер пластической зоны можно представить в форме ряда:
Здесь - челны числовой последовательности Эйлера. В случае можно использовать
где -коэффициент интенсивности напряжений для трещины длиной 2l.
Слайд 7
Для расчёта перемещений вычисляется функция Вестергардера для случая «а» и для случая
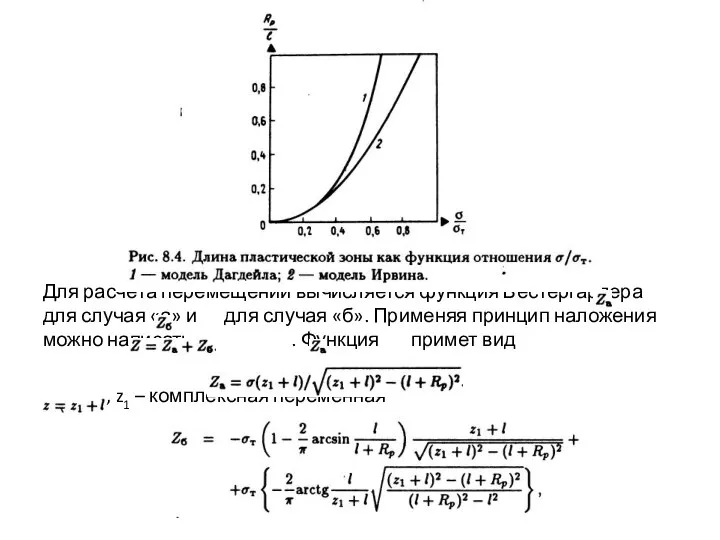
«б». Применяя принцип наложения можно написать . Функция примет вид
, z1 – комплексная переменная






 Практическая №3
Практическая №3 Состав и строение атома
Состав и строение атома Потужність
Потужність Особенности частотного планирования сотовых сетей цифровой радиосвязи
Особенности частотного планирования сотовых сетей цифровой радиосвязи Классификация тепловых двигателей
Классификация тепловых двигателей Электрический ток. Частицы ядра (протоны и нейтроны)
Электрический ток. Частицы ядра (протоны и нейтроны) Презентация на тему Электромагнит
Презентация на тему Электромагнит  Творческое объединение авиаторы
Творческое объединение авиаторы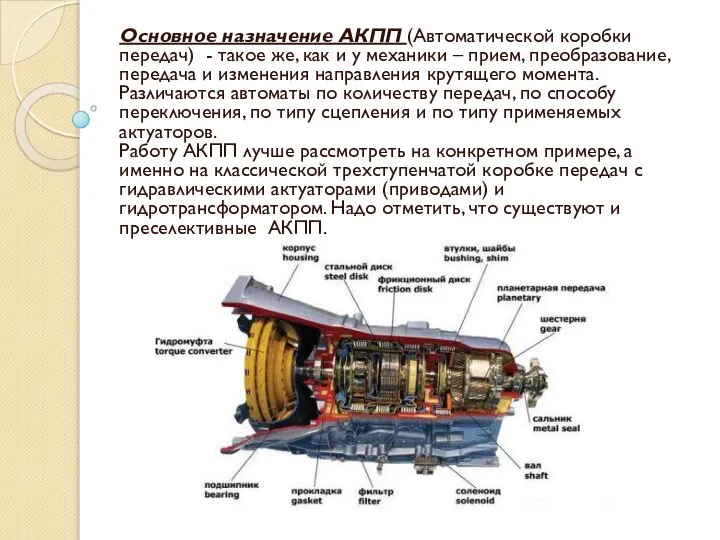 obshchee-ustroystvo-i-printsip-raboty-akpp
obshchee-ustroystvo-i-printsip-raboty-akpp Механические волны. Лекция 9
Механические волны. Лекция 9 Презентация на тему Строение вещества
Презентация на тему Строение вещества  Обобщение курса физики
Обобщение курса физики Работа в электростатическом поле
Работа в электростатическом поле Непрерывные модели
Непрерывные модели Презентация (1)
Презентация (1) Звуковые волны
Звуковые волны Шлифовальные станки
Шлифовальные станки Магнитное поле
Магнитное поле Сила Лоренца
Сила Лоренца 2Методы расчетов электрических нагрузок и выбор сечения проводников
2Методы расчетов электрических нагрузок и выбор сечения проводников Материаловедение и технологии конструкционных материалов
Материаловедение и технологии конструкционных материалов 1-ая лекция
1-ая лекция Динамика. Масса и сила
Динамика. Масса и сила Расчет средней энергии нормальных колебаний кристаллической решетки
Расчет средней энергии нормальных колебаний кристаллической решетки Как заставить тела двигаться?
Как заставить тела двигаться? Квантовая теория электромагнитного излучения и вещества
Квантовая теория электромагнитного излучения и вещества Молекулярная физика
Молекулярная физика Электростатика. Электрические схемы. Проверочный тест
Электростатика. Электрические схемы. Проверочный тест