Содержание
- 2. Существует и другой способ описания поля – с помощью потенциала. Однако для этого необходимо сначала доказать,
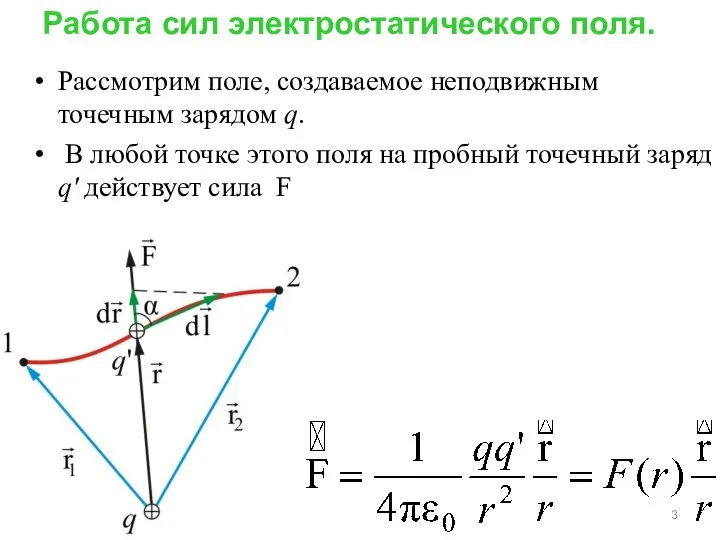
- 3. Рассмотрим поле, создаваемое неподвижным точечным зарядом q. В любой точке этого поля на пробный точечный заряд
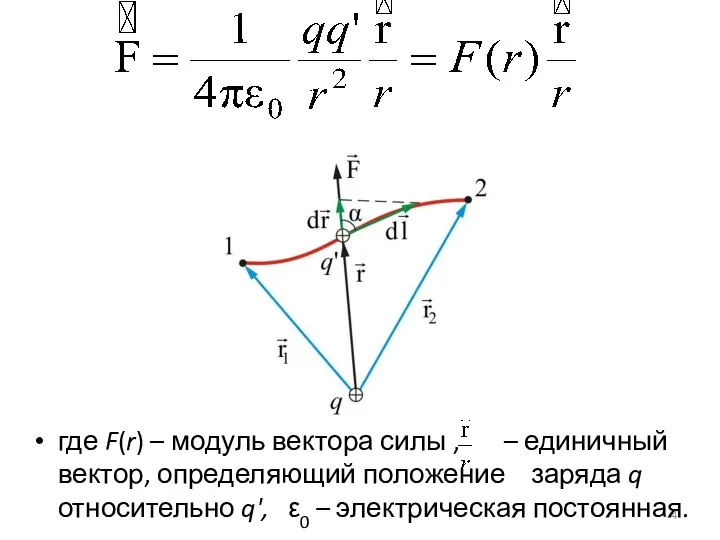
- 4. где F(r) – модуль вектора силы , – единичный вектор, определяющий положение заряда q относительно q',
- 5. Для того, чтобы доказать, что электростатическое поле потенциально, нужно доказать, что силы электростатического поля консервативны. Из
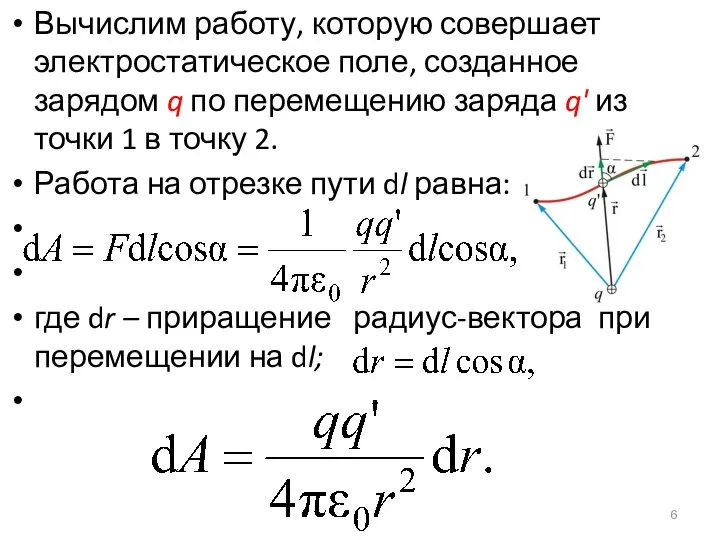
- 6. Вычислим работу, которую совершает электростатическое поле, созданное зарядом q по перемещению заряда q' из точки 1
- 7. Полная работа при перемещении из точки 1 в точку 2 равна интегралу:
- 8. Работа электростатических сил не зависит от формы пути, а только лишь от координат начальной и конечной
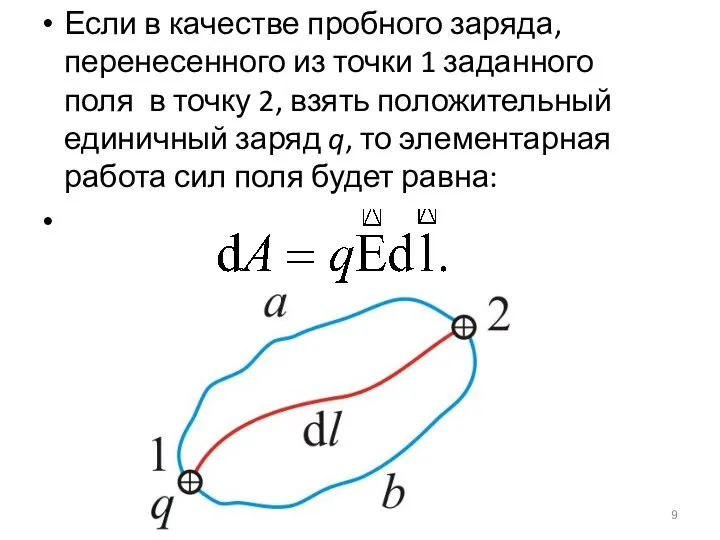
- 9. Если в качестве пробного заряда, перенесенного из точки 1 заданного поля в точку 2, взять положительный
- 10. Тогда вся работа равна: Такой интеграл по замкнутому контуру называется циркуляцией вектора Из независимости линейного интеграла
- 11. Для доказательства теоремы разобьем произвольно замкнутый путь на две части: 1а2 и 2b1. Из сказанного выше
- 12. Теорема о циркуляции позволяет сделать ряд важных выводов, практически не прибегая к расчетам. Рассмотрим простой пример,
- 13. Работа и потенциальная энергия электростатическое поле потенциально. Следовательно, можно ввести функцию состояния, зависящую от координат –
- 14. Исходя из принципа суперпозиции сил , можно показать, что общая работа А будет равна сумме работ
- 15. Работу сил электростатического поля можно выразить через убыль потенциальной энергии – разность двух функций состояний: Это
- 16. Потенциал. Разность потенциалов Разные пробные заряды q',q'',… будут обладать в одной и той же точке поля
- 17. Подставив в выражение для потенциала значение потенциальной энергии , получим выражение для потенциала точечного заряда: Потенциал,
- 18. физический смысл имеет не потенциал, а разность потенциалов, поэтому договорились считать, что потенциал точки, удаленной в
- 19. Другое определение потенциала: т.е. потенциал численно равен работе, которую совершают силы поля над единичным положительным зарядом
- 20. Если поле создается системой зарядов, то, используя принцип суперпозиции, получаем: Тогда и для потенциала или т.е.
- 21. Выразим работу сил электростатического поля через разность потенциалов между начальной и конечной точками: Таким образом, работа
- 22. Формулу можно использовать для установления единиц потенциала: за единицу потенциала принимают потенциал в такой точке поля,
- 23. Производными единицами эВ являются МэВ, ГэВ и ТэВ: 1 МэВ = 106 эВ = 1,60⋅10−13 Дж,
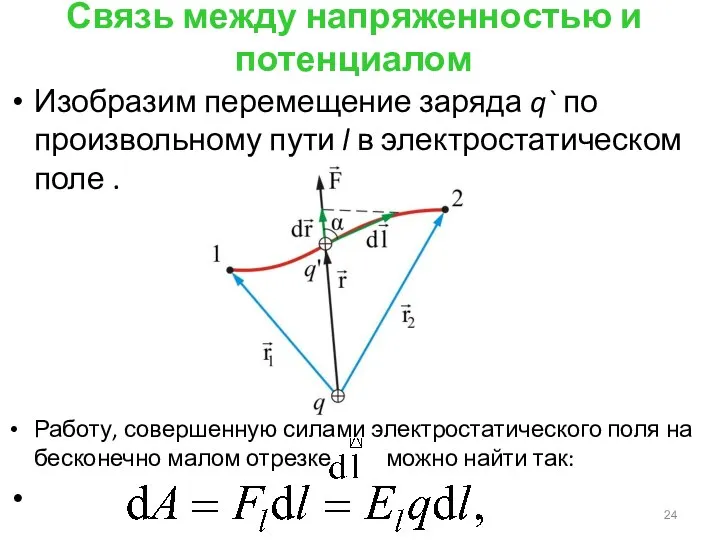
- 24. Связь между напряженностью и потенциалом Изобразим перемещение заряда q` по произвольному пути l в электростатическом поле
- 25. С другой стороны, эта работа, равна убыли потенциальной энергии заряда, перемещенного на расстоянии dl: отсюда
- 26. Для ориентации dl (направление перемещения) в пространстве, надо знать проекции на оси координат: Определение градиента: сумма
- 27. Коротко связь между и φ записывается так: или так: где (набла) означает символический вектор, называемый оператором
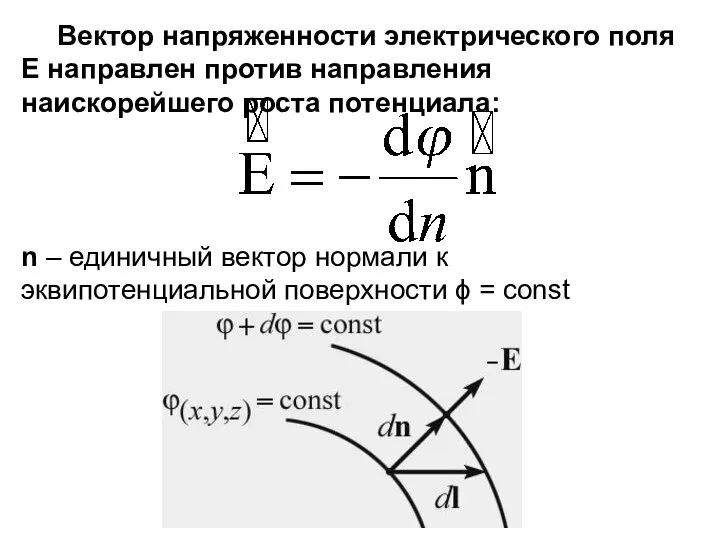
- 28. Вектор напряженности электрического поля Е направлен против направления наискорейшего роста потенциала: n – единичный вектор нормали
- 29. Безвихревой характер электростатического поля Из условия следует одно важное соотношение, а именно, величина, векторного произведения для
- 30. Величина называется ротором или вихрем Мы получаем важнейшее уравнение электростатики: электростатическое поле – безвихревое.
- 31. Согласно теореме Стокса, присутствует следующая связь между контурным и поверхностным интегралами: где контур L ограничивающий поверхность
- 32. Силовые линии и эквипотенциальные поверхности Направление силовой линии (линии напряженности) в каждой точке совпадает с направлением
- 33. Воображаемая поверхность, все точки которой имеют одинаковый потенциал, называется эквипотенциальной поверхностью. Уравнение этой поверхности
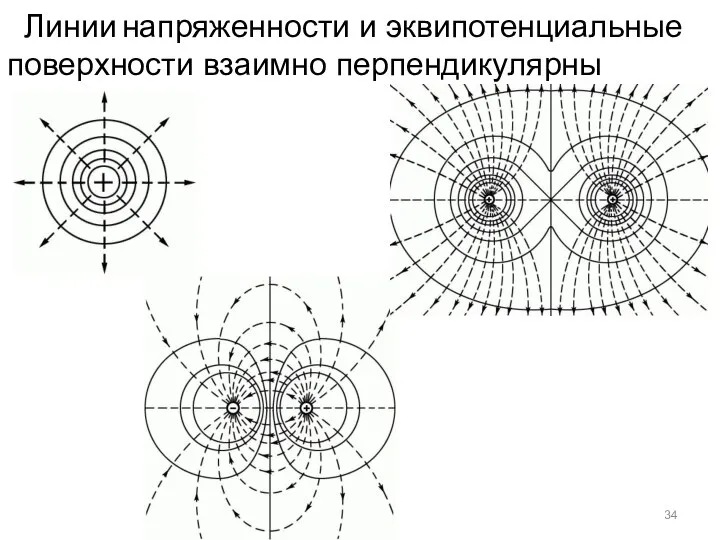
- 34. Линии напряженности и эквипотенциальные поверхности взаимно перпендикулярны
- 35. Формула выражает связь потенциала с напряженностью и позволяет по известным значениям φ найти напряженность поля в
- 36. Интеграл можно брать по любой линии, соединяющие точку 1 и точку 2, ибо работа сил поля
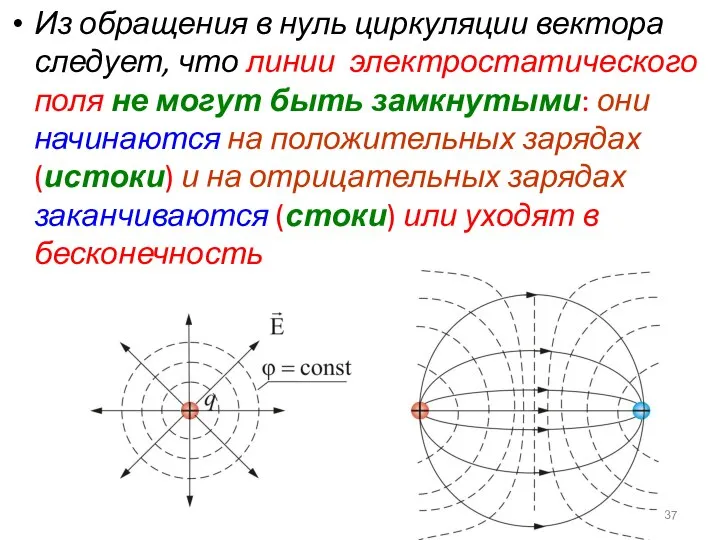
- 37. Из обращения в нуль циркуляции вектора следует, что линии электростатического поля не могут быть замкнутыми: они
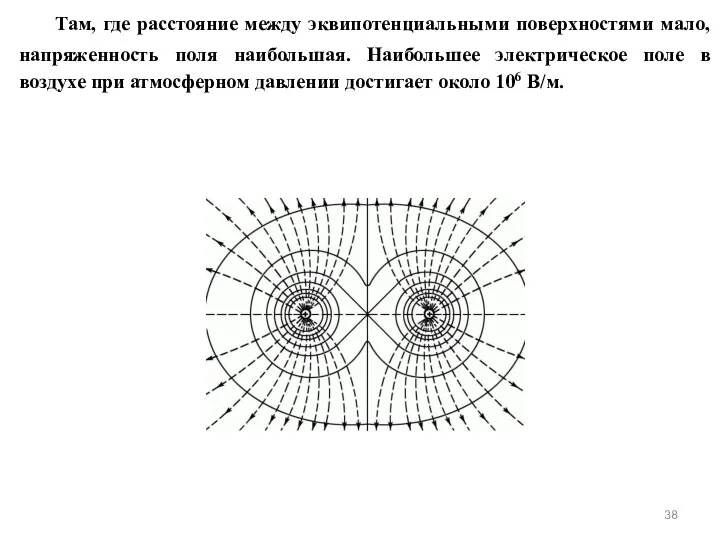
- 38. Там, где расстояние между эквипотенциальными поверхностями мало, напряженность поля наибольшая. Наибольшее электрическое поле в воздухе при
- 39. Расчет потенциалов простейших электростатических полей Рассмотрим несколько примеров вычисления разности потенциалов между точками поля, созданного некоторыми
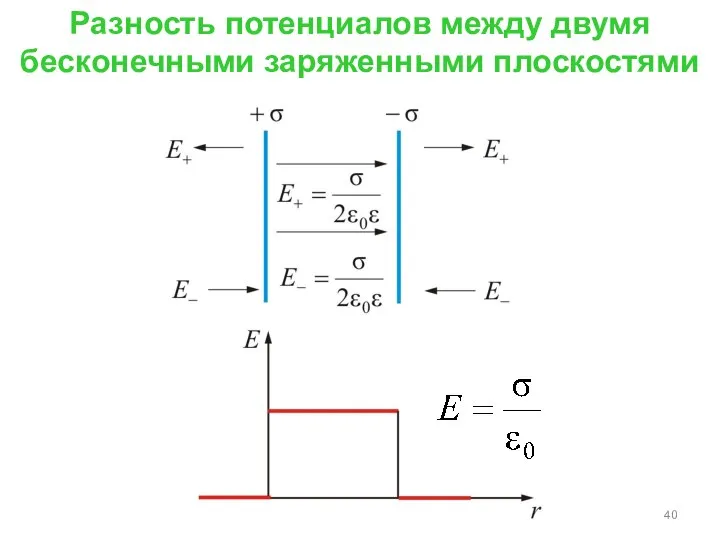
- 40. Разность потенциалов между двумя бесконечными заряженными плоскостями
- 41. Мы показали, что напряженность связана с потенциалом отсюда где – напряженность электростатического поля между заряженными плоскостями
- 42. Чтобы получить выражение для потенциала между плоскостями, проинтегрируем выражение При x1 = 0 и x2 =
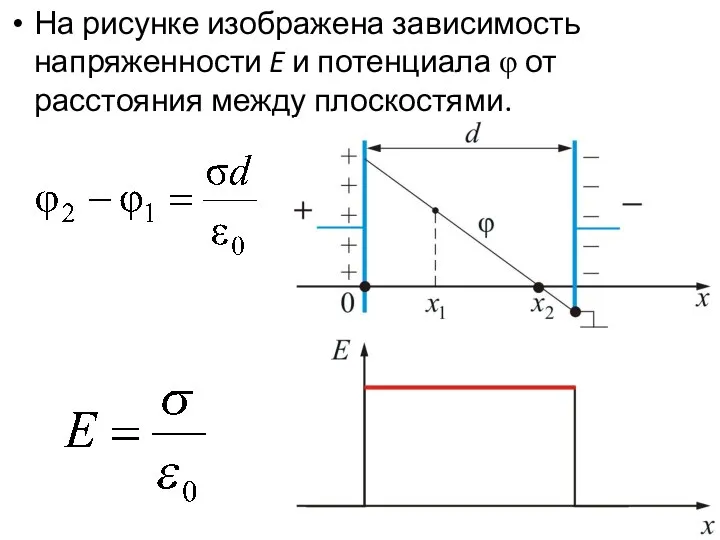
- 43. На рисунке изображена зависимость напряженности E и потенциала φ от расстояния между плоскостями.
- 44. Разность потенциалов между точками поля, образованного бесконечно длинной цилиндрической поверхностью С помощью теоремы Остроградского-Гаусса мы показали,
- 45. Тогда,т.к. отсюда следует, что разность потенциалов в произвольных точках 1 и 2 будет равна:
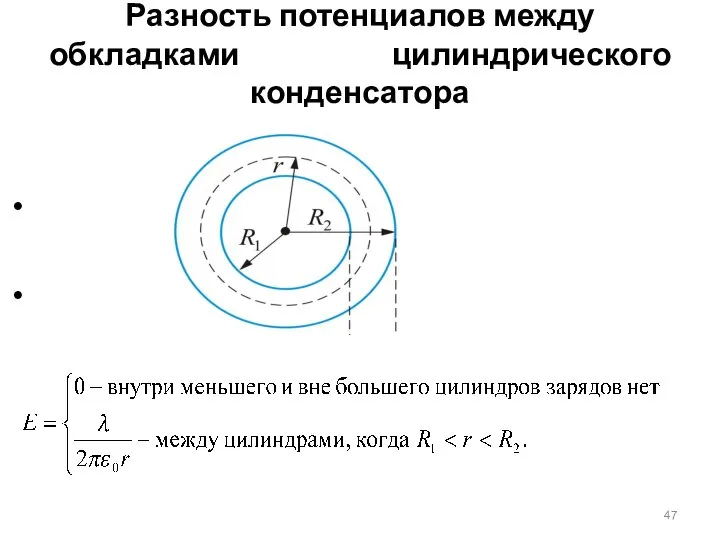
- 47. Разность потенциалов между обкладками цилиндрического конденсатора
- 48. Т.к. , то
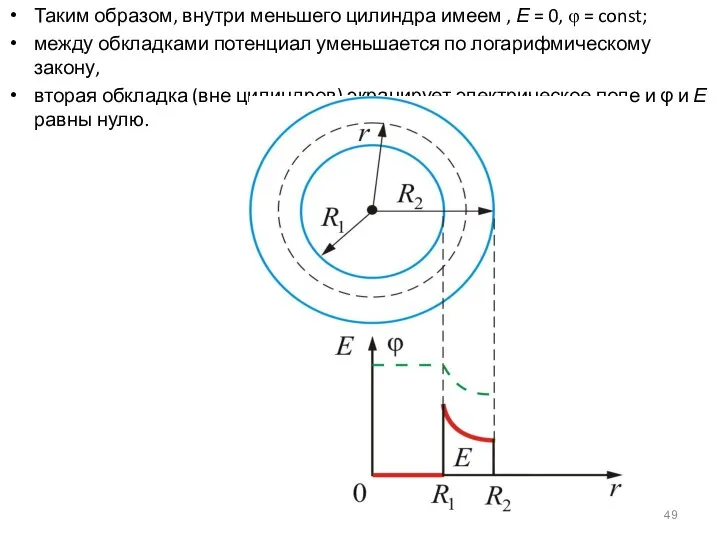
- 49. Таким образом, внутри меньшего цилиндра имеем , Е = 0, φ = const; между обкладками потенциал
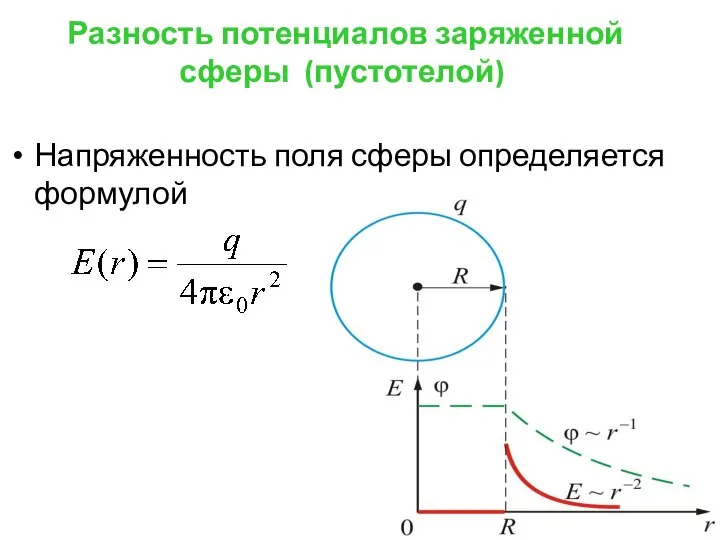
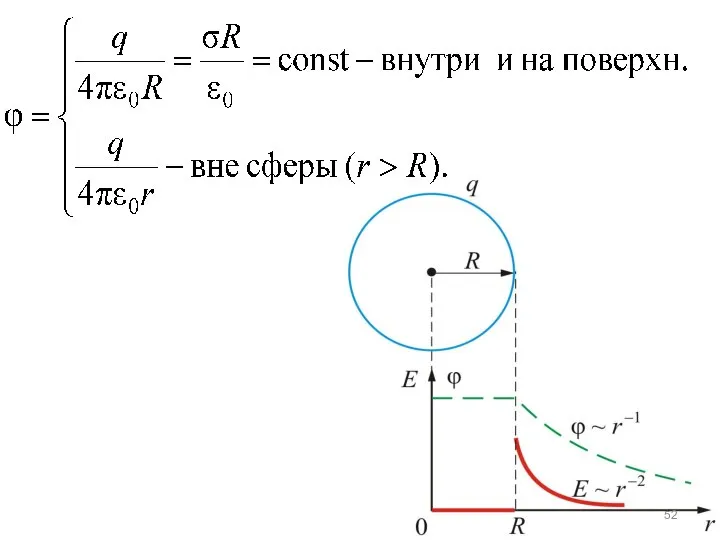
- 50. Разность потенциалов заряженной сферы (пустотелой) Напряженность поля сферы определяется формулой
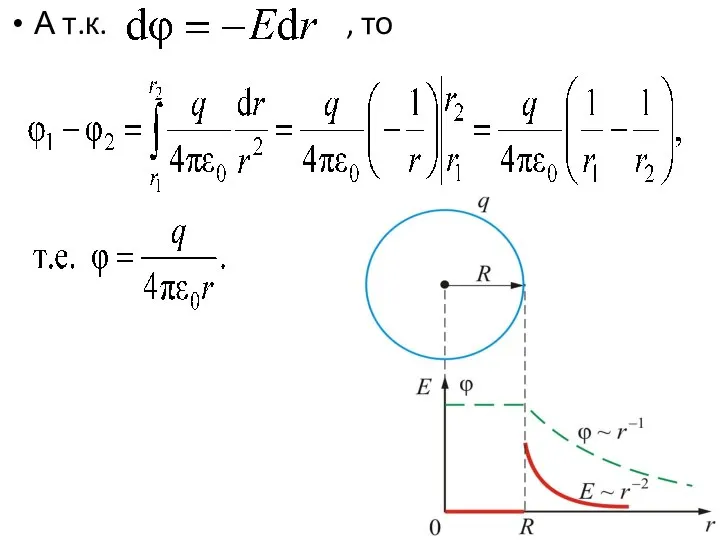
- 51. А т.к. , то
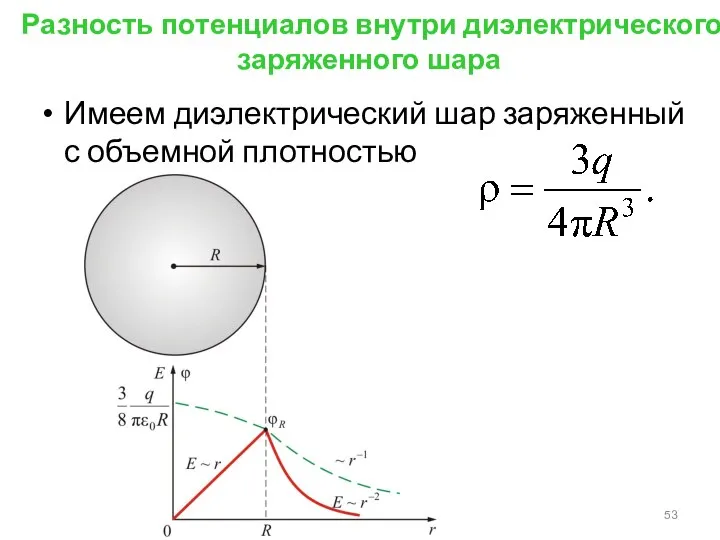
- 53. Разность потенциалов внутри диэлектрического заряженного шара Имеем диэлектрический шар заряженный с объемной плотностью
- 54. Напряженность поля шара, вычисленная с помощью теоремы Остроградского-Гаусса:
- 55. Отсюда найдем разность потенциалов шара: или
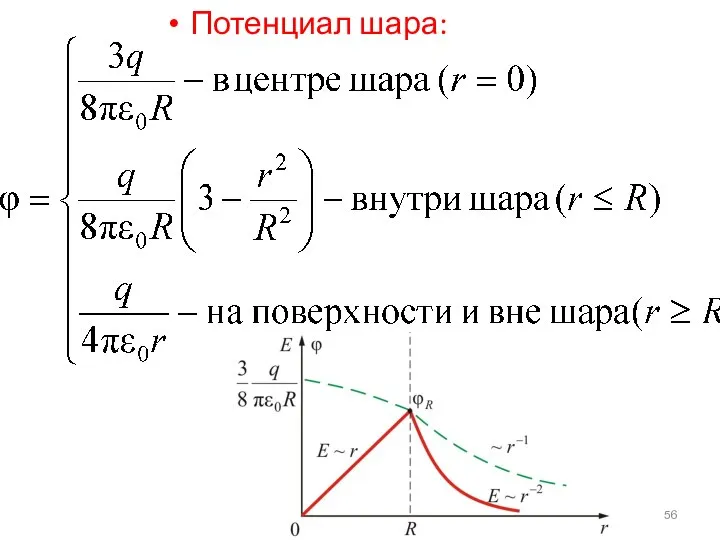
- 56. Потенциал шара:
- 58. Скачать презентацию


















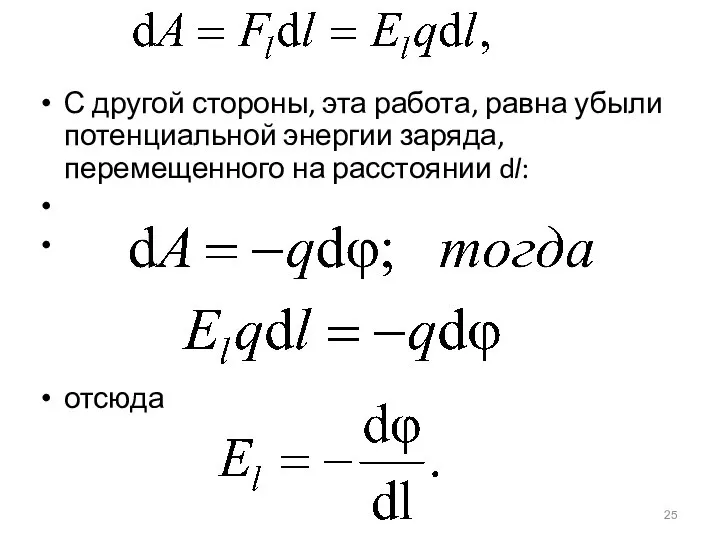


















 Презентация на тему Давление твёрдых тел, жидкостей и газов
Презентация на тему Давление твёрдых тел, жидкостей и газов  Презентация на тему Поле чудес Галилео Галилей
Презентация на тему Поле чудес Галилео Галилей  Кинематические характеристики движения
Кинематические характеристики движения Плавание тел. Условие плавания тел
Плавание тел. Условие плавания тел Радиоактивный распад. Алгоритм скорости распада
Радиоактивный распад. Алгоритм скорости распада Молекулярная физика. Основные положения молекулярно-кинетической теории
Молекулярная физика. Основные положения молекулярно-кинетической теории Методы измерения фокусных расстояний
Методы измерения фокусных расстояний Выпускная квалификационная работа: Проектирование шиномонтажного участка АТП
Выпускная квалификационная работа: Проектирование шиномонтажного участка АТП Первые предсказания погоды. Отто фон Герике. Барометр
Первые предсказания погоды. Отто фон Герике. Барометр Второй закон Ньютона. Динамика материальной точки
Второй закон Ньютона. Динамика материальной точки Машины и оборудование, инженерные системы и энергосберегающие технологии в городском хозяйстве и сфере услуг
Машины и оборудование, инженерные системы и энергосберегающие технологии в городском хозяйстве и сфере услуг Презентация на тему Снег
Презентация на тему Снег  Радиоволны. История открытия
Радиоволны. История открытия Методы исследования частиц
Методы исследования частиц Электрические цели. Работа тока
Электрические цели. Работа тока Давление
Давление III Инженерная олимпиада им.Н.А.Зайцева
III Инженерная олимпиада им.Н.А.Зайцева Ремонт ходовой части. Ремонт электрооборудования
Ремонт ходовой части. Ремонт электрооборудования Аэрогель
Аэрогель Почему летает бумажный самолетик и как сделать, чтобы он летал еще лучше?
Почему летает бумажный самолетик и как сделать, чтобы он летал еще лучше? Конструкторско-технологическое обеспечение машиностроительных производств профиль технология машиностроения
Конструкторско-технологическое обеспечение машиностроительных производств профиль технология машиностроения Электрическая цепь и ее составные
Электрическая цепь и ее составные Потенциальная энергия заряженного тела
Потенциальная энергия заряженного тела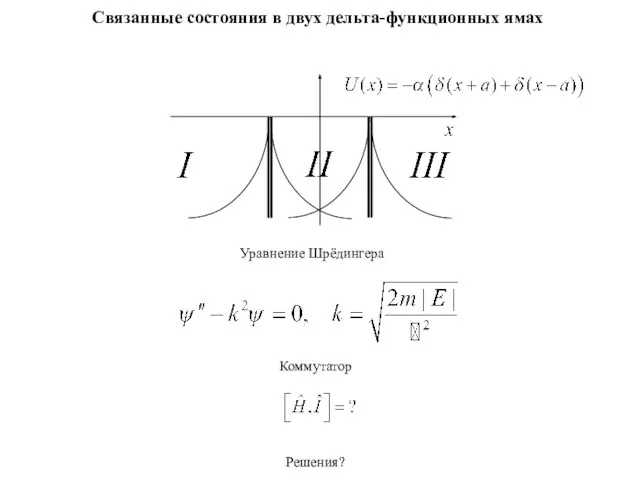 Связанные состояния в двух дельта - функционных ямах
Связанные состояния в двух дельта - функционных ямах Физические явления. Наблюдения и опыт
Физические явления. Наблюдения и опыт Введение. Кинематика
Введение. Кинематика Звуковые волны
Звуковые волны Фізичні основи оптикоелектронних систем. Тема 2
Фізичні основи оптикоелектронних систем. Тема 2