Содержание
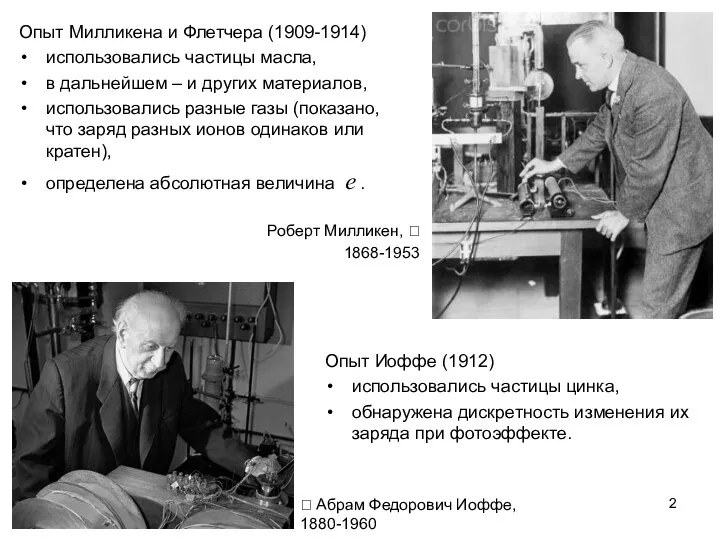
- 2. Опыт Милликена и Флетчера (1909-1914) использовались частицы масла, в дальнейшем – и других материалов, использовались разные
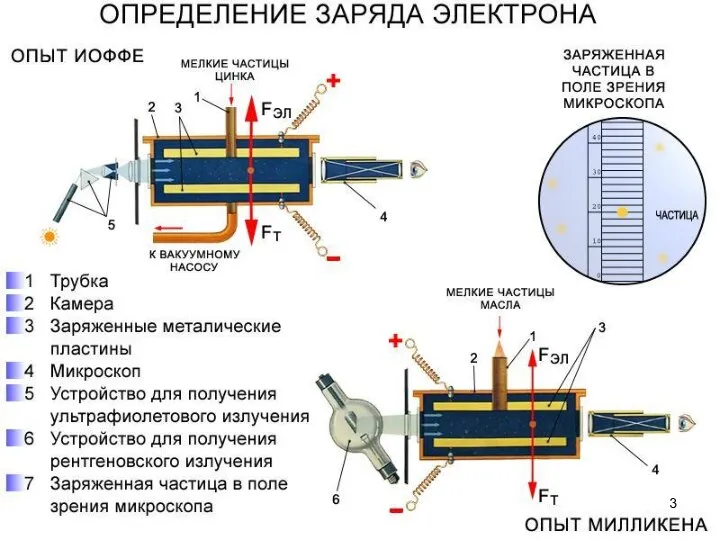
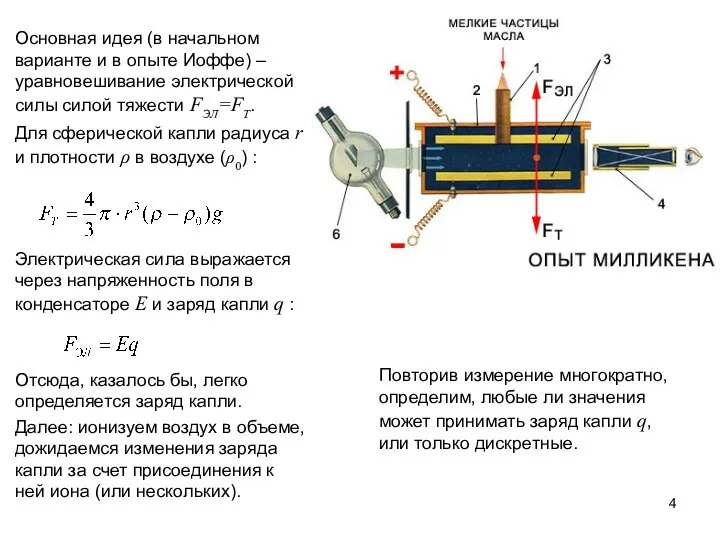
- 4. Основная идея (в начальном варианте и в опыте Иоффе) – уравновешивание электрической силы силой тяжести FЭЛ=FT.
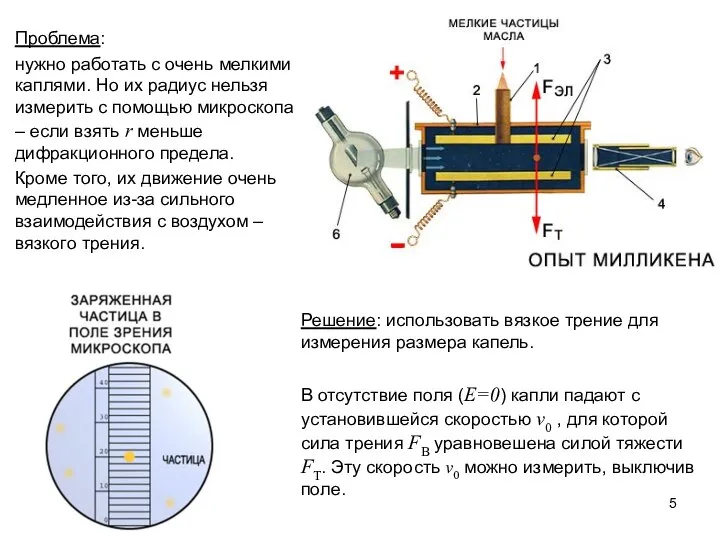
- 5. Проблема: нужно работать с очень мелкими каплями. Но их радиус нельзя измерить с помощью микроскопа –
- 6. Формула Стокса для сферы радиуса r , движущейся со скоростью v в среде с вязкостью η:
- 7. Подставив (*) и (**), получим выражение в окончательном виде: Все величины в правой части были известны
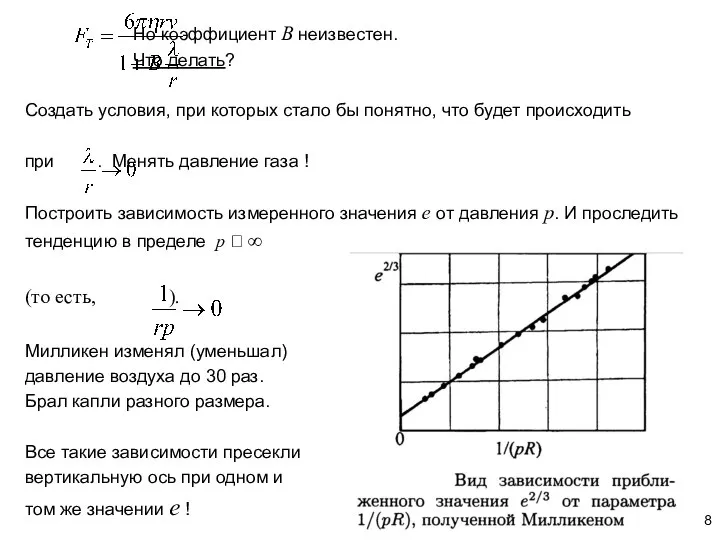
- 8. Но коэффициент B неизвестен. Что делать? Создать условия, при которых стало бы понятно, что будет происходить
- 10. Скачать презентацию


 Тормозное управление
Тормозное управление Петля КМПЦ
Петля КМПЦ Векторная физическая величина сила
Векторная физическая величина сила Занимательная физика. Задачи
Занимательная физика. Задачи Проектирование зоны ТО-2 для парка автомобилей Volvo FM 6730
Проектирование зоны ТО-2 для парка автомобилей Volvo FM 6730 Магнитное взаимодействие
Магнитное взаимодействие Постоянные магниты
Постоянные магниты Дви́гатель вну́треннего сгора́ния (ДВС)
Дви́гатель вну́треннего сгора́ния (ДВС) Глубокая яма
Глубокая яма ОМиУОИ_л1
ОМиУОИ_л1 Презентация на тему Шкала электромагнитных волн
Презентация на тему Шкала электромагнитных волн  Физика вокруг нас Подготовили: обучающиеся 10 класса
Физика вокруг нас Подготовили: обучающиеся 10 класса Технология обработки на металлорежущих станках. Элементы резьбы
Технология обработки на металлорежущих станках. Элементы резьбы Балочные системы. Определение реакций опор. (Тема 1.4.1)
Балочные системы. Определение реакций опор. (Тема 1.4.1) Техническое обслуживание и ремонт электрических машин постоянного и переменного тока. Тест
Техническое обслуживание и ремонт электрических машин постоянного и переменного тока. Тест Логические элементы
Логические элементы Основные законы электрической цепи постоянного тока
Основные законы электрической цепи постоянного тока Применение зондовых методов для локальной модификации поверхности
Применение зондовых методов для локальной модификации поверхности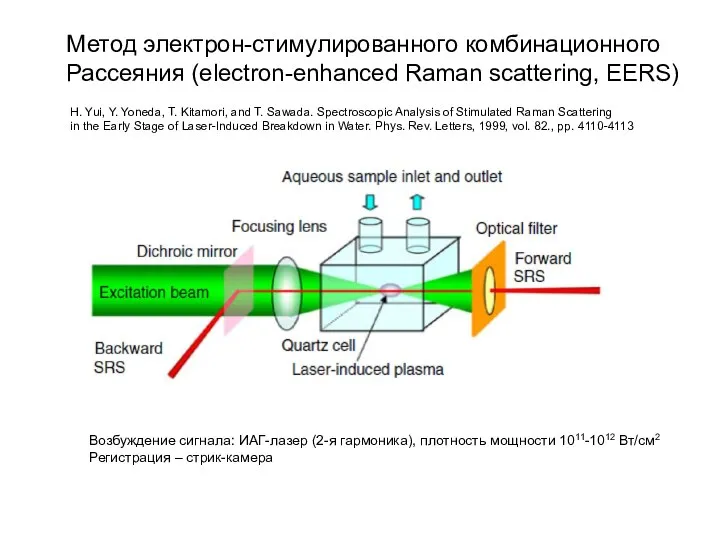 Метод электрон-стимулированного комбинационного Рассеяния (electron-enhanced Raman scattering, EERS)
Метод электрон-стимулированного комбинационного Рассеяния (electron-enhanced Raman scattering, EERS) Принципы радиосвязи
Принципы радиосвязи Электромагнетизм
Электромагнетизм Модель атома Томсона
Модель атома Томсона Центр тяжести тел. Условия равновесия тел
Центр тяжести тел. Условия равновесия тел Плоская система пар сил и условие её равновесия
Плоская система пар сил и условие её равновесия Диффузия газов 2.2.1
Диффузия газов 2.2.1 Презентация на тему Магнитное поле катушки с током. Электромагниты
Презентация на тему Магнитное поле катушки с током. Электромагниты  Механические передачи. Цепные передачи. (Лекция 3)
Механические передачи. Цепные передачи. (Лекция 3) Управляющие процессы и их формализованное описание
Управляющие процессы и их формализованное описание