Разветвленные цепи переменного тока

Для анализа и расчета разветвленных цепей переменного тока используют проводимости, с помощью которых разветвленную цепь можно преобразовать в простейшую цепь и аналитически рассчитать токи и напряжения всех ее участков.

В цепях переменного тока существуют три проводимости
Полная;
активная;
и реактивная. причем только полная проводимость является величиной, обратной полному сопротивлению последовательного участка цепи.

Выражения проводимостей в цепях переменного тока:
Ток в каждом неразветвленном участке цепи раскладывают на две составляющие, одна из которых есть проекция на вектор напряжения (активная составляющая тока Ia ), а другая - на линию, перпендикулярную вектору напряжения (реактивная составляющая тока Iр ).
Активная составляющая тока определяет активную мощность
P = UI cos φ = UIa ;
реактивная составляющая тока - реактивную мощность
Q = UI sin φ = UIр.

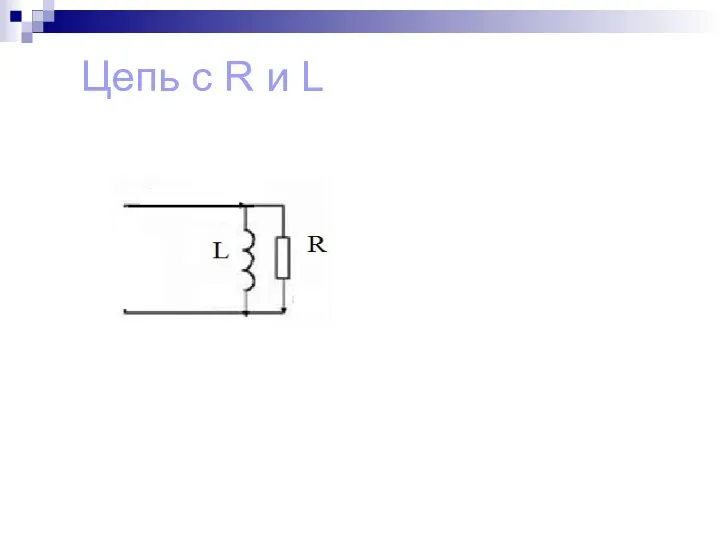
Активная проводимость
активная составляющая тока I1 равна
I1a = I1 cos φ1= Ur1/z12 = Ug1
Величина g1 = r1/z12 называется активной проводимостью ветви

Реактивная проводимость
Реактивная составляющая тока I1 равна
Ilp = I1 sin φ1 = UxL/z12 = Ub1.
Величина b1 = xL/z12 называется реактивной проводимостью ветви

Полная проводимость
Выразив составляющие тока через напряжение и проводимости, получим
I1 = √(Ug1)2 + (UbL1)2 = U √g12 + bL12 = Uу1 = U/z1,
где у1 = 1/z1 = √g12 + bL12 — полная проводимость ветви.

Определение типа нагрузки
Необходимо отметить, что если
ΣbL > ΣbC, то эквивалентное сопротивление хэ будет индуктивным, если ΣbC > ΣbL —емкостным.

Цепь с R и L

Ток в ветви с индуктивностью
Ток Ilp = I1 sin φ1 = UxL/z12 = UbL1
Проводимость bL1 = xL/z12 =1/ХL1

Ток в ветви с активным сопротивлением
Ток I2а = I2cos φ2 = Ug2 ;
Проводимость g2 =r /z22 =1/R ;

Вектор общего тока цепи
равен геометрической сумме векторов токов Ī1 и Ī2:
Ī = Ī1 + Ī2
Ī = Īа + Īр =ŪgR + ŪbL

Цепь с R и C

Ток в ветви с активным сопротивлением
Ток I1a = I1 cos φ1 = Ur1/z12 = Ug1
Проводимость g1 = r1/z12 =1/R

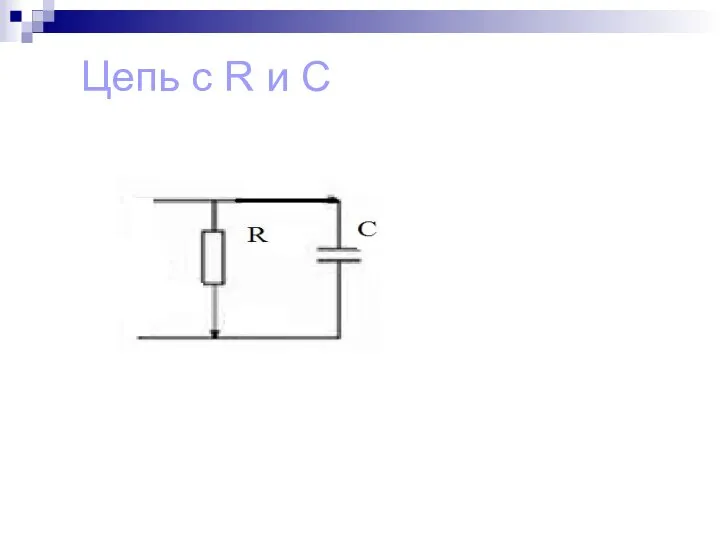
Ток в ветви с емкостью
Ток I2p = I2 sin φ2 = U b2 ;
Проводимость b2 = bC2 = xC2 /z22=1/ Xc

Вектор общего тока цепи равен геометрической сумме векторов токов Ī1 и Ī2:
Ī = Ī1 + Ī2
Īа + Īр = ŪgR + Ūbc

Задача

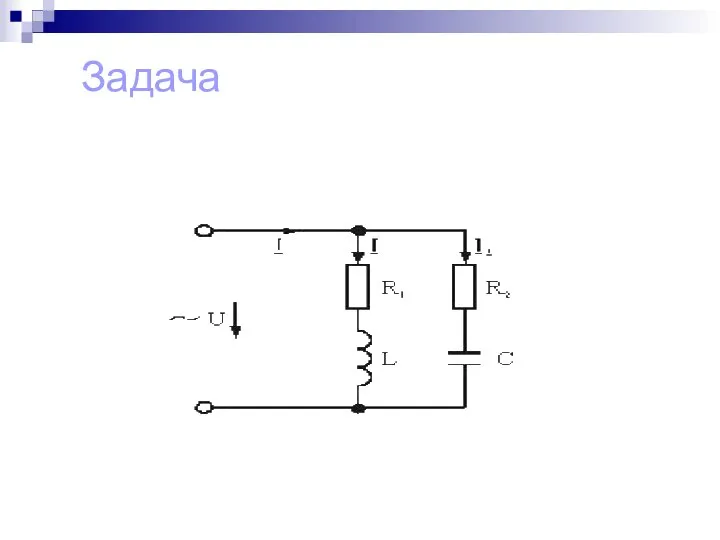
Расчет цепи при смешанном соединении может быть произведен путем замены ее простейшей эквивалентной цепью. Для этого вначале определяют активные, реактивные и полные проводимости параллельно включенных ветвей: g1, g2, b1, b2, у1, у2.

Затем находят эквивалентные активную, реактивную и полную проводимости параллельного участка цепи:
gэ = g1+ g2;
bэ = b1 + b2;
уэ = √gэ2 + bэ2.

Далее определяют эквивалентные активное, реактивное и полное сопротивления параллельного участка цепи:
rэ = gэzэ2; xэ = bэzэ2; zэ = 1/уэ.
В результате расчетов цепь может быть заменена эквивалентной цепью, где все сопротивления включены последовательно.

Общие активное, реактивное и полное сопротивления цепи равны
rоб = rэ + r.
xоб = x ± xэ,
zоб = √rоб2 + xоб2.
Цепь приобретает простейший вид. Общий ток цепи определяют по закону Ома:
I = U/zоб

Напряжение между точками а и b
Uab = Izэ = I/уэ .
Токи в параллельных ветвях равны I1 = Uab у1, I2 = Uab у2.