Содержание
- 2. Сечения реакции При прохождении через вещество частицы взаимодействуют с атомами, из которых оно состоит, т. е.
- 3. Сечения реакций Когда сталкиваются две субатомные частицы (например, α-частица и ядро золота в опыте Резерфорда), между
- 4. Сечения реакций Основной величиной, которой оперируют физики, исследующие столкновение микрообъектов, является эффективное сечение или просто сечение
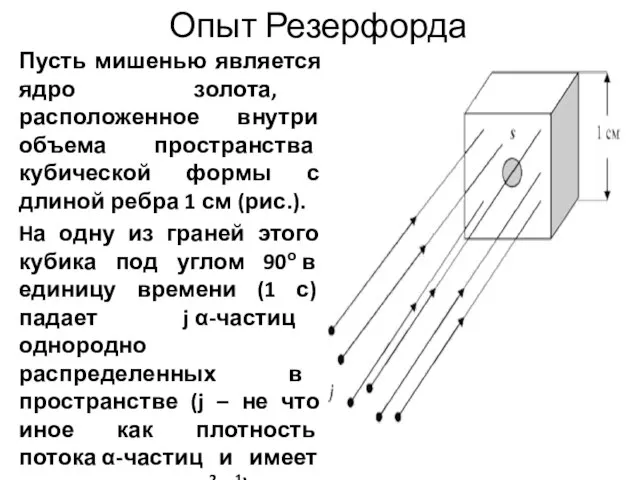
- 5. Опыт Резерфорда Пусть мишенью является ядро золота, расположенное внутри объема пространства кубической формы с длиной ребра
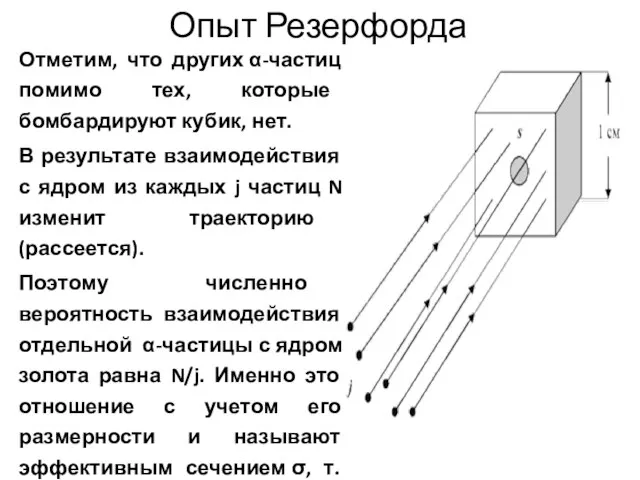
- 6. Опыт Резерфорда Отметим, что других α-частиц помимо тех, которые бомбардируют кубик, нет. В результате взаимодействия с
- 7. Опыт Резерфорда Происхождение словосочетания “поперечное эффективное сечение” можно пояснить следующим примером. При механическом соударении двух шаров,
- 8. Сечение реакции Для взаимодействий, не являющихся механическими (контактными), σ - эффективная площадь, характеризующая вероятность конкретного процесса.
- 9. Сечение реакции N = j n S l σ = j M σ, (2) где σ
- 10. Сечение реакции Понятие σ используют как для характеристики вероятности реакции между частицами a + b →
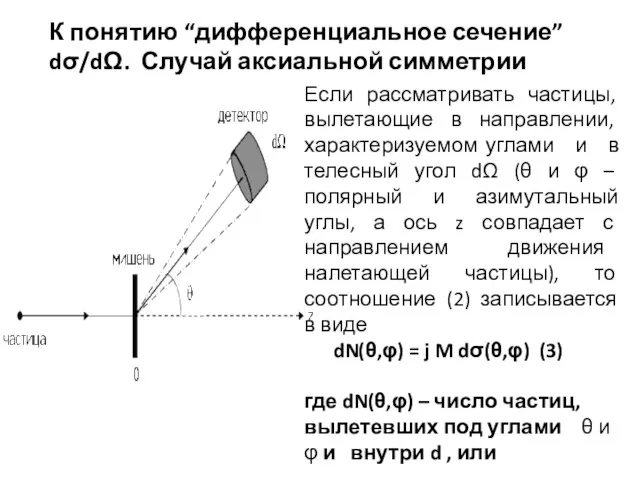
- 11. К понятию “дифференциальное сечение” dσ/dΩ. Случай аксиальной симметрии Если рассматривать частицы, вылетающие в направлении, характеризуемом углами
- 12. К понятию “дифференциальное сечение” dσ/dΩ. Случай аксиальной симметрии (4) Величина dσ/dΩ = σ(θ,φ) называется дифференциальным сечением,
- 13. Сечение реакции В случае кулоновского рассеяния частицы с энергией E и зарядом Z1 на тяжелом точечном
- 14. Сечение реакции Если, помимо углов вылета продуктов реакции, определять их энергию, то можно найти вероятность процесса,
- 15. Сечение реакции Очевидно, ещё большая детализация наших знаний о реакции требует использования понятий трижды, четырежды и
- 16. Эта величина с одной стороны имеет тот же физический смысл, что и в классической механике, то
- 17. ни в пределах объёма ядра, ни вблизи элементарной частицы нет такой области, при пересечении которой другой
- 18. эффективные сечения определяются не столько геометрическими размерами сложных микрочастиц или радиусами действия сил, сколько волновыми свойствами
- 19. Поскольку λ обратно пропорциональна скорости, сечение возрастает при убывании энергии. Однако связанные состояния образуются при строгих
- 20. Единицы измерения В СИ – м2. В СГС – см2. Внесистемная единица – барн (б) 1
- 21. Макроскопическое сечение Макроскопическое сечение Σij i-го процесса для j-го нуклида в среде можно определить как произведение
- 22. Макроскопическое сечение σij — это число взаимодействий i-го типа в единицу времени в единице объёма j-го
- 23. Макроскопическое сечение Если вещество представляет собой гомогенную смесь различных ядер, то макроскопическое сечение смеси определяют как
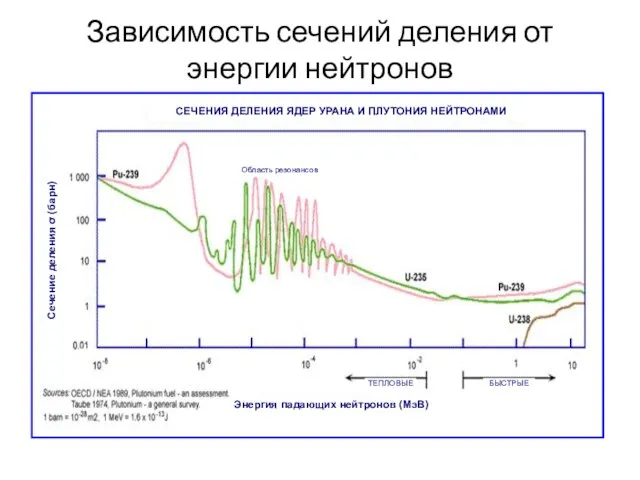
- 24. Зависимость сечений деления от энергии нейтронов
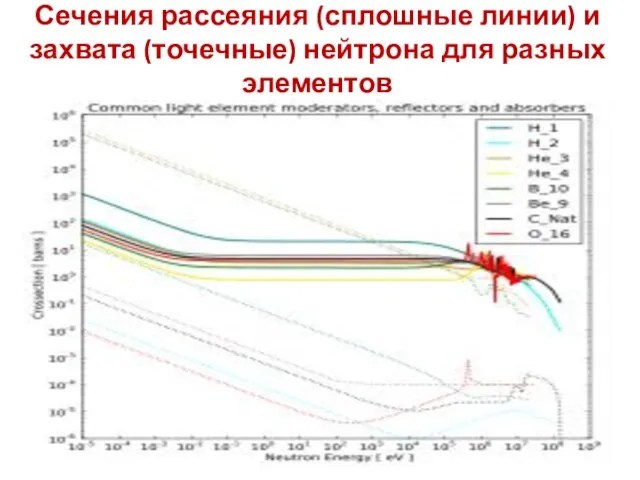
- 25. Сечения рассеяния (сплошные линии) и захвата (точечные) нейтрона для разных элементов
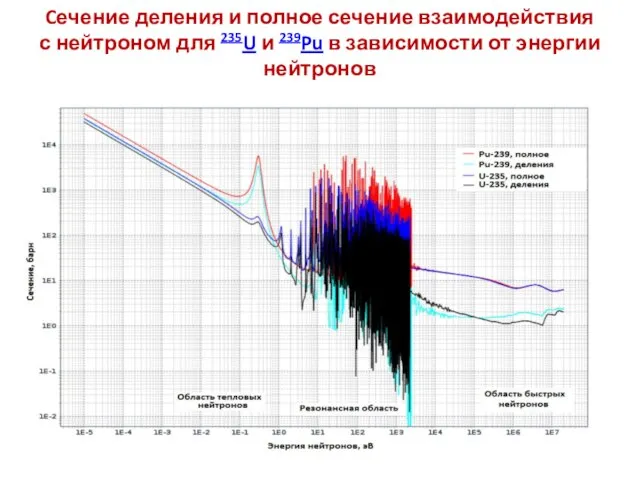
- 26. Cечение деления и полное сечение взаимодействия с нейтроном для 235U и 239Pu в зависимости от энергии
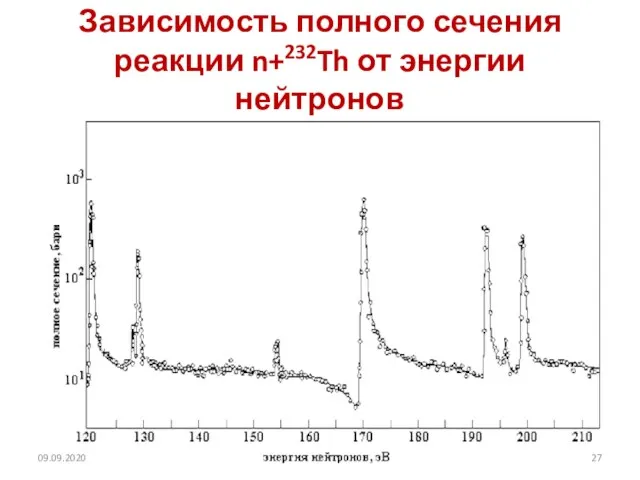
- 27. Зависимость полного сечения реакции n+232Th от энергии нейтронов 09.09.2020 2
- 28. Базы экспериментальных сечений и библиотеки оцененных ядерных NEA — Nuclear Data Services — Evaluated Nuclear Data
- 29. Боровская теория ядерных реакций. Сечение ядерной реакции, идущей через составное ядро Многие реакции взаимодействия ядер с
- 30. Боровская теория ядерных реакций. Сечение ядерной реакции, идущей через составное ядро a + A → C
- 31. Боровская теория ядерных реакций. Сечение ядерной реакции, идущей через составное ядро Превращения составного ядра С могут
- 32. Радиационный захват Если энергия возбуждения составного ядра меньше энергии отделения от него какой-либо частицы, то происходит
- 33. Другие каналы Другим каналом «распада» 236U* является его деление на осколки. Многообразие вариантов деления с испусканием
- 34. Вероятность протекания реакции Каждый канал превращения составного ядра, находящегося в возбужденном состоянии, характеризуется своей вероятностью wb.
- 35. Вероятность протекания реакции Если обозначить σaC сечение образования составного ядра C, то сечение σab реакции по
- 36. Вероятность протекания реакции Тогда σb′b = wbσb′C Это значит, что отношения сечений по каждому из каналов
- 37. Угловое распределение продуктов реакции Угловое распределение продуктов реакции в системе центра инерции симметрично относительно угла χ
- 39. Скачать презентацию





























 Организация технического обслуживания и ремонта системы питания дизельного двигателя Mitsubishi L200
Организация технического обслуживания и ремонта системы питания дизельного двигателя Mitsubishi L200 Методы наблюдения и регистрации элементарных частиц
Методы наблюдения и регистрации элементарных частиц Влияние накипи на энергетические и денежные затраты
Влияние накипи на энергетические и денежные затраты Явление инерция. Инерция покоя. Инерция движения
Явление инерция. Инерция покоя. Инерция движения Навигация по геофизическим полям
Навигация по геофизическим полям Ламповый генератор
Ламповый генератор Теория функционала плотности: война с бесконечностью
Теория функционала плотности: война с бесконечностью Досліди Фарадея. Явище електромагнітної індукції. 9кл
Досліди Фарадея. Явище електромагнітної індукції. 9кл ЭДС индукции в движущихся проводниках. Решение задач
ЭДС индукции в движущихся проводниках. Решение задач Работа и мощность электрического тока. Закон Джоуля-Ленца. КПД источника тока
Работа и мощность электрического тока. Закон Джоуля-Ленца. КПД источника тока Презентация на тему Изменение агрегатного состояния вещества
Презентация на тему Изменение агрегатного состояния вещества  Презентация на тему Действие магнитного поля на проводники с током (11 класс)
Презентация на тему Действие магнитного поля на проводники с током (11 класс)  Методы наблюдения и регистрации элементарных частиц
Методы наблюдения и регистрации элементарных частиц Изображения, даваемые линзой
Изображения, даваемые линзой Задачи по ТМ. Сложение ускорений
Задачи по ТМ. Сложение ускорений Электромагнитные колебания
Электромагнитные колебания Дифракция световых волн
Дифракция световых волн Простые механизмы. Момент силы. Золотое правило механики. 7 класс
Простые механизмы. Момент силы. Золотое правило механики. 7 класс Инструменты и приборы
Инструменты и приборы Следствия из преобразований Лоренца. Сложение скоростей в специальной теории относительности. Релятивистская динамика
Следствия из преобразований Лоренца. Сложение скоростей в специальной теории относительности. Релятивистская динамика Принцип Гюйгенса. Дифракция механических волн
Принцип Гюйгенса. Дифракция механических волн Фізика. Запитання для оцінювання
Фізика. Запитання для оцінювання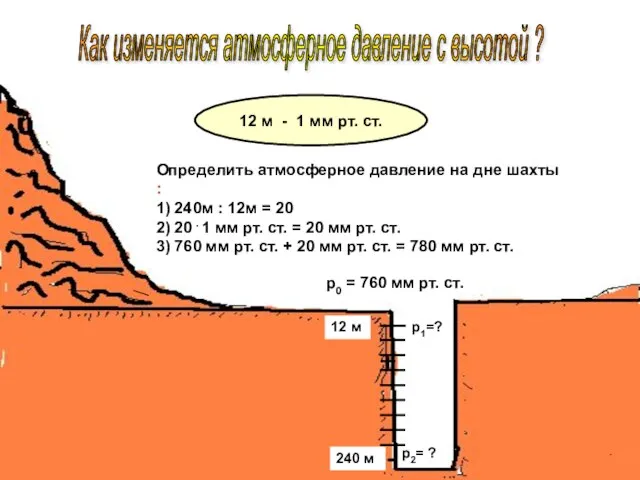 Презентация по физике "Как изменяется атмосферное давление с высотой ?" -
Презентация по физике "Как изменяется атмосферное давление с высотой ?" -  Классификация связей в динамике
Классификация связей в динамике Ядерное оружие
Ядерное оружие Закон Ома для участка цепи. Сопротивление. Последовательное и параллельное соединение проводников
Закон Ома для участка цепи. Сопротивление. Последовательное и параллельное соединение проводников Электромагнитная природа света
Электромагнитная природа света Физическая викторина. Игра
Физическая викторина. Игра