Содержание
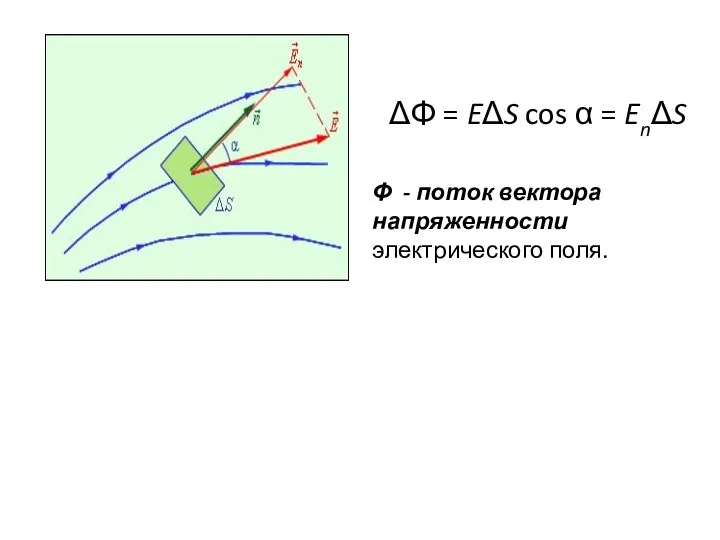
- 2. ΔΦ = EΔS cos α = EnΔS Φ - поток вектора напряженности электрического поля.
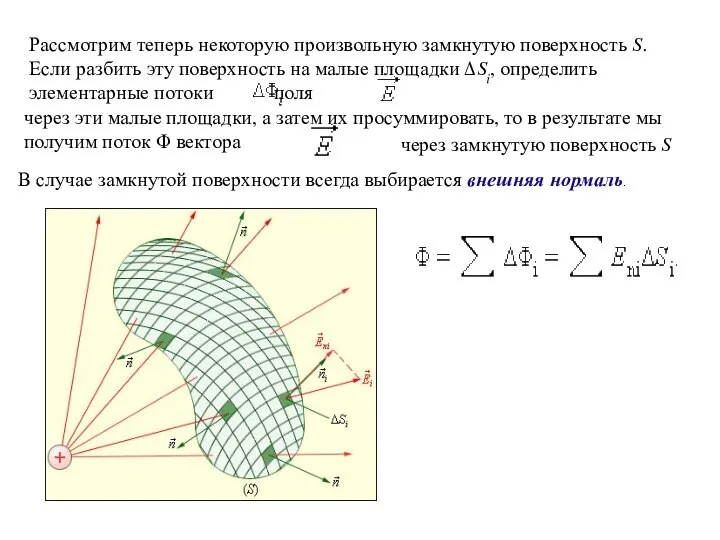
- 3. Рассмотрим теперь некоторую произвольную замкнутую поверхность S. Если разбить эту поверхность на малые площадки ΔSi, определить
- 4. Теорема Гаусса утверждает: Поток вектора напряженности электростатического поля через произвольную замкнутую поверхность равен алгебраической сумме зарядов,
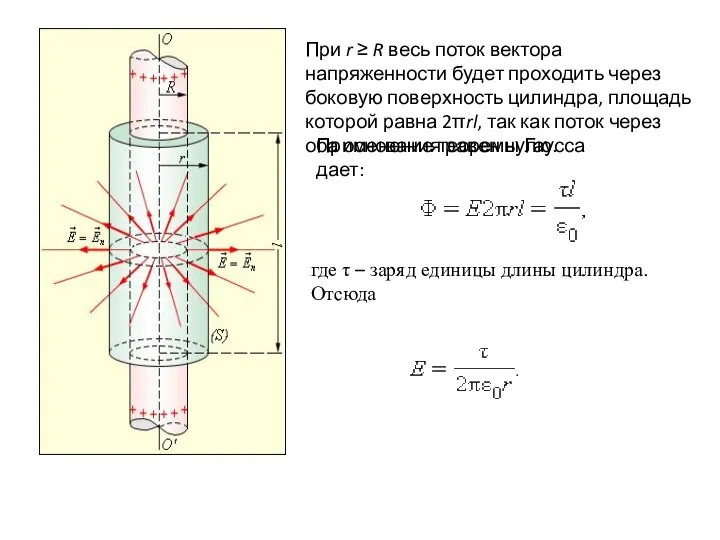
- 5. Используя теорему Гаусса, можно в ряде случаев легко вычислить напряженность электрического поля вокруг заряженного тела, если
- 6. При r ≥ R весь поток вектора напряженности будет проходить через боковую поверхность цилиндра, площадь которой
- 8. Скачать презентацию


 Частицы
Частицы Оптические приборы
Оптические приборы Работа локомотивной бригады
Работа локомотивной бригады Презентация на тему Физика в картинках
Презентация на тему Физика в картинках  Электрическое поле. Однородное и неоднородное электрическое поле. Напряженность электрического поля
Электрическое поле. Однородное и неоднородное электрическое поле. Напряженность электрического поля Электрическая система. Процесс
Электрическая система. Процесс Опыт Резерфорда по рассеянию альфа-частиц. Постулаты Бора. Опыты Франка и Герца. Понятие о нелинейной оптике. Лазеры. Волновые
Опыт Резерфорда по рассеянию альфа-частиц. Постулаты Бора. Опыты Франка и Герца. Понятие о нелинейной оптике. Лазеры. Волновые zamena_t_kolodok
zamena_t_kolodok Сила тяжести
Сила тяжести Лекция 5. Флуорофоры для оптического имиджинга
Лекция 5. Флуорофоры для оптического имиджинга Физика. 10 класс
Физика. 10 класс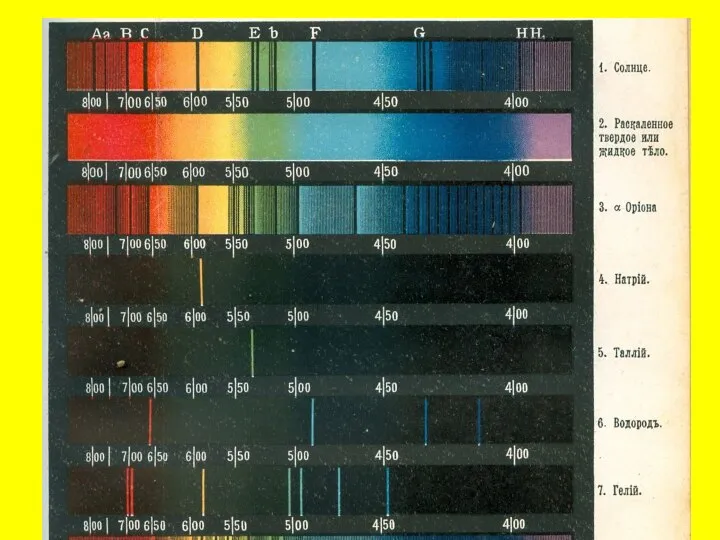 Radiation (излучения)
Radiation (излучения) Условия плавания тел
Условия плавания тел c38d9b8
c38d9b8 Анализ ЭМВ Н- И Е--типов в круглом волноводе
Анализ ЭМВ Н- И Е--типов в круглом волноводе Исследовательская работа по физике на тему: Искусственные источники света и их практическая ценность. Автор: Дуров Лев 9б класс Н
Исследовательская работа по физике на тему: Искусственные источники света и их практическая ценность. Автор: Дуров Лев 9б класс Н Электричество и магнетизм. Лекция № 3
Электричество и магнетизм. Лекция № 3 Измерение физических величин
Измерение физических величин Взаимодействие проводников с током
Взаимодействие проводников с током Кинематика. Занятие 4
Кинематика. Занятие 4 Работа измерительного прибора ИРК-ПРО
Работа измерительного прибора ИРК-ПРО Сцепление ГАЗ 53-12. Урок №70
Сцепление ГАЗ 53-12. Урок №70 Нелинейные эффекты в средах с квадратичной нелинейностью. Лекция 2
Нелинейные эффекты в средах с квадратичной нелинейностью. Лекция 2 Резка металла слесарной ножовкой
Резка металла слесарной ножовкой Поиск эффективных способов преобразования энергии морских волн в энергию поступательного движения судна
Поиск эффективных способов преобразования энергии морских волн в энергию поступательного движения судна Своя игра на тему: Физика и химия в медицине
Своя игра на тему: Физика и химия в медицине Энергия - основа мироздания. Солнечные батареи
Энергия - основа мироздания. Солнечные батареи Уход за швейной машиной
Уход за швейной машиной