Содержание
- 2. ДИНАМИКА ТОЧКИ 14.2 ОБЩИЕ СВЕДЕНИЯ Динамика - это раздел механики, в котором изучается движение материальных точек,
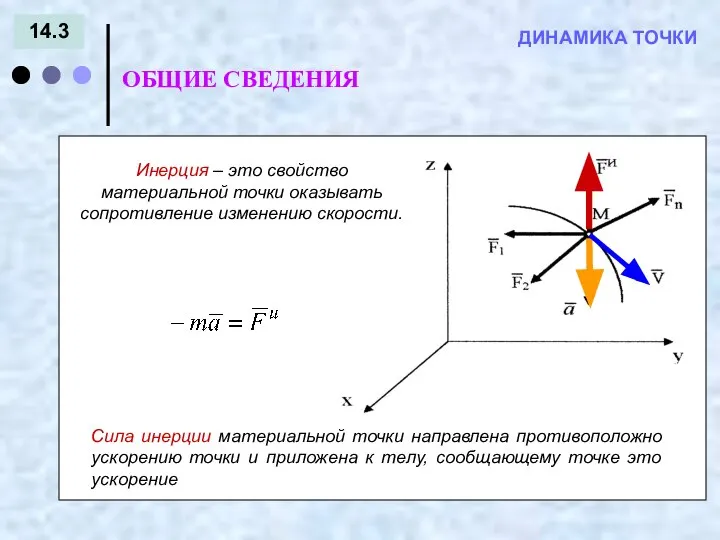
- 3. 14.3 ОБЩИЕ СВЕДЕНИЯ ДИНАМИКА ТОЧКИ
- 4. 14.4 Дифференциальные уравнения движения материальной точки Дифференциальные уравнения движения точки в проекциях на декартовые оси: ДИНАМИКА
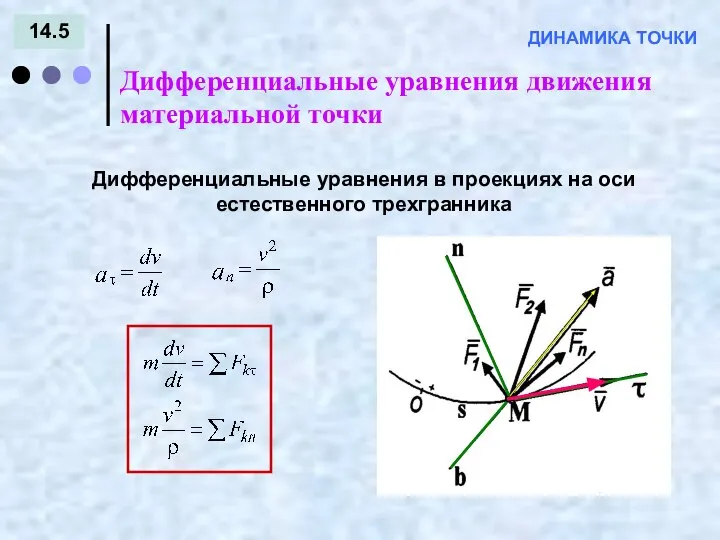
- 5. 14.5 Дифференциальные уравнения движения материальной точки ДИНАМИКА ТОЧКИ Дифференциальные уравнения в проекциях на оси естественного трехгранника
- 6. 15.2 Дифференциальные уравнения движения материальной точки ДИНАМИКА ТОЧКИ ДВЕ ЗАДАЧИ ДИНАМИКИ Первая задача динамики: по известному
- 7. 15.3 Дифференциальные уравнения движения материальной точки ДИНАМИКА ТОЧКИ Решение задач динамики точки: Первая задача динамики: Вторая
- 8. 15.4 Дифференциальные уравнения движения материальной точки ДИНАМИКА ТОЧКИ Лифт весом Р начинает подъем по закону: y
- 9. 15.5 Дифференциальные уравнения движения материальной точки ДИНАМИКА ТОЧКИ Найти: закон движения точки при начальных условиях: t=0,
- 10. 16.2 Дифференциальные уравнения движения материальной точки ДИНАМИКА ТОЧКИ Свободные прямолинейные колебания материальной точки Сила сопротивления R,
- 11. 16.3 Дифференциальные уравнения движения материальной точки ДИНАМИКА ТОЧКИ Свободные прямолинейные колебания материальной точки если c/m =
- 12. 16.4 Дифференциальные уравнения движения материальной точки ДИНАМИКА ТОЧКИ Характеристическое уравнение: x = ent Свободные прямолинейные колебания
- 13. 16.5 Дифференциальные уравнения движения материальной точки ДИНАМИКА ТОЧКИ Свободные прямолинейные колебания материальной точки A - амплитуда
- 14. 16.6 Дифференциальные уравнения движения материальной точки ДИНАМИКА ТОЧКИ Влияние постоянной силы на свободные колебания точки P=
- 15. 17.2 ТЕОРЕМА О ДВИЖЕНИИ ЦЕНТРА МАСС ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ Введение в динамику системы Механическая система -
- 16. 17.3 ТЕОРЕМА О ДВИЖЕНИИ ЦЕНТРА МАСС ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ Центр масс механической системы Центром масс (центром
- 17. 17.4 ТЕОРЕМА О ДВИЖЕНИИ ЦЕНТРА МАСС ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ Дифференциальные уравнения движения центра масс в проекциях
- 18. 17.5 ТЕОРЕМА О ДВИЖЕНИИ ЦЕНТРА МАСС ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ Закон сохранения движения центра масс 1. Пусть
- 19. 17.6 ТЕОРЕМА О ДВИЖЕНИИ ЦЕНТРА МАСС ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ Примеры применения теоремы о движении центра масс
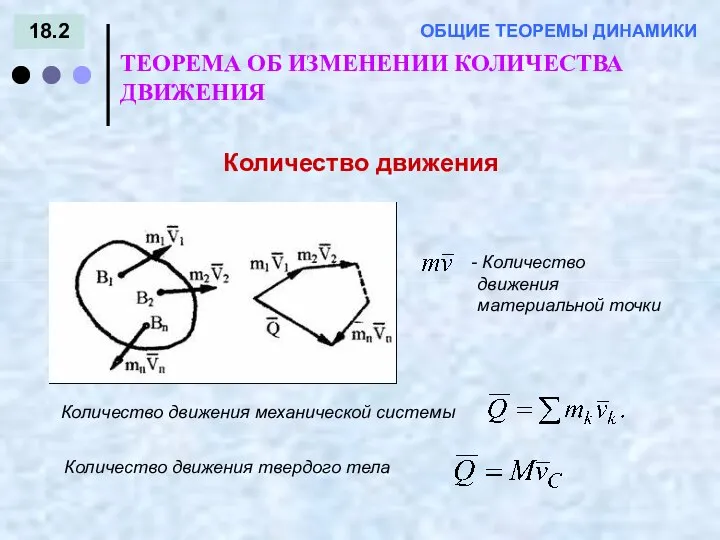
- 20. 18.2 ТЕОРЕМА ОБ ИЗМЕНЕНИИ КОЛИЧЕСТВА ДВИЖЕНИЯ ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ Количество движения Количество движения механической системы Количество
- 21. 18.3 ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ Импульс силы ТЕОРЕМА ОБ ИЗМЕНЕНИИ КОЛИЧЕСТВА ДВИЖЕНИЯ Единицей измерения импульса силы в
- 22. 18.4 ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ ТЕОРЕМА ОБ ИЗМЕНЕНИИ КОЛИЧЕСТВА ДВИЖЕНИЯ Дифференциальное уравнение движения точки
- 23. 18.5 ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ ТЕОРЕМА ОБ ИЗМЕНЕНИИ КОЛИЧЕСТВА ДВИЖЕНИЯ Для всех точек механической системы Теорема об
- 24. 17.10 ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ Закон сохранения количества движения ТЕОРЕМА ОБ ИЗМЕНЕНИИ КОЛИЧЕСТВА ДВИЖЕНИЯ
- 25. 19.2 ТЕОРЕМА ОБ ИЗМЕНЕНИИ КИНЕТИЧЕСКОГО МОМЕНТА ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ Осевые моменты инерции тела Iz=∑mkhk2 ρ -
- 26. 19.3 ТЕОРЕМА ОБ ИЗМЕНЕНИИ КИНЕТИЧЕСКОГО МОМЕНТА ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ Момент количества движения материальной точки
- 27. 19.4 ТЕОРЕМА ОБ ИЗМЕНЕНИИ КИНЕТИЧЕСКОГО МОМЕНТА ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ Теорема об изменении момента количества движения точки
- 28. 20.2 ТЕОРЕМА ОБ ИЗМЕНЕНИИ КИНЕТИЧЕСКОГО МОМЕНТА ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ Кинетический момент системы Кинетический момент вращающегося тела
- 29. 20.3 ТЕОРЕМА ОБ ИЗМЕНЕНИИ КИНЕТИЧЕСКОГО МОМЕНТА ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ Теорема об изменении кинетического момента механической системы
- 30. 20.4 ТЕОРЕМА ОБ ИЗМЕНЕНИИ КИНЕТИЧЕСКОГО МОМЕНТА ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ следствия из теоремы:
- 31. 20.5 ТЕОРЕМА ОБ ИЗМЕНЕНИИ КИНЕТИЧЕСКОГО МОМЕНТА ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ Дифференциальное уравнение вращения тела вокруг неподвижной оси
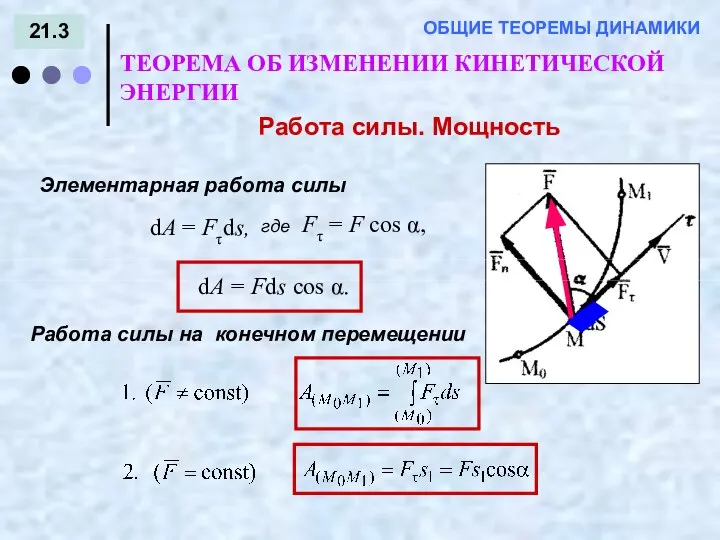
- 32. 21.3 ТЕОРЕМА ОБ ИЗМЕНЕНИИ КИНЕТИЧЕСКОЙ ЭНЕРГИИ ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ Работа силы. Мощность Элементарная работа силы Работа
- 33. 21.4 ТЕОРЕМА ОБ ИЗМЕНЕНИИ КИНЕТИЧЕСКОЙ ЭНЕРГИИ ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ Работа силы. Мощность Если вектор силы спроецировать
- 34. 21.5 ТЕОРЕМА ОБ ИЗМЕНЕНИИ КИНЕТИЧЕСКОЙ ЭНЕРГИИ ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ Примеры вычисления работы Работа силы тяжести z0
- 35. 21.6 ТЕОРЕМА ОБ ИЗМЕНЕНИИ КИНЕТИЧЕСКОЙ ЭНЕРГИИ ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ Работа силы. Мощность Работа силы упругости F
- 36. 21.7 ТЕОРЕМА ОБ ИЗМЕНЕНИИ КИНЕТИЧЕСКОЙ ЭНЕРГИИ ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ Работа силы. Мощность Работа силы, приложенной к
- 37. 22.2 ТЕОРЕМА ОБ ИЗМЕНЕНИИ КИНЕТИЧЕСКОЙ ЭНЕРГИИ ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ для материальной точки Кинетическая энергия Единица измерения
- 38. 22.3 ТЕОРЕМА ОБ ИЗМЕНЕНИИ КИНЕТИЧЕСКОЙ ЭНЕРГИИ ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ Кинетическая энергия для твердого тела Поступательное движение
- 39. 22.4 ТЕОРЕМА ОБ ИЗМЕНЕНИИ КИНЕТИЧЕСКОЙ ЭНЕРГИИ ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ maτ = ∑Fkτ. Рассмотрим материальную точку с
- 41. Скачать презентацию


































 Основы обеспечения микроклимата
Основы обеспечения микроклимата Сила трения. Викторина
Сила трения. Викторина Презентация на тему Равновесие тел
Презентация на тему Равновесие тел  Применение фотоэффекта
Применение фотоэффекта Электротехника. Практические работы. 6 класс
Электротехника. Практические работы. 6 класс Поляризация. Лекция 29
Поляризация. Лекция 29 Повторение. Физика атомного ядра
Повторение. Физика атомного ядра Законы сохранения в механике
Законы сохранения в механике Основы термодинамики
Основы термодинамики Презентация по физике "Техника безопасности в кабинете физики" -
Презентация по физике "Техника безопасности в кабинете физики" -  Электромагнитное поле
Электромагнитное поле Фотоэффект. Опыты А.Г. Столетова (1888-1889)
Фотоэффект. Опыты А.Г. Столетова (1888-1889) Внедрение гибридных солнечно-ветровых систем электропитания для развития ИКТ в предгорных населенных пунктах и регионах
Внедрение гибридных солнечно-ветровых систем электропитания для развития ИКТ в предгорных населенных пунктах и регионах Условия плавания тел
Условия плавания тел Динамика. Масса и сила
Динамика. Масса и сила Электростатика вакуума и проводников
Электростатика вакуума и проводников zakony_Nyutona
zakony_Nyutona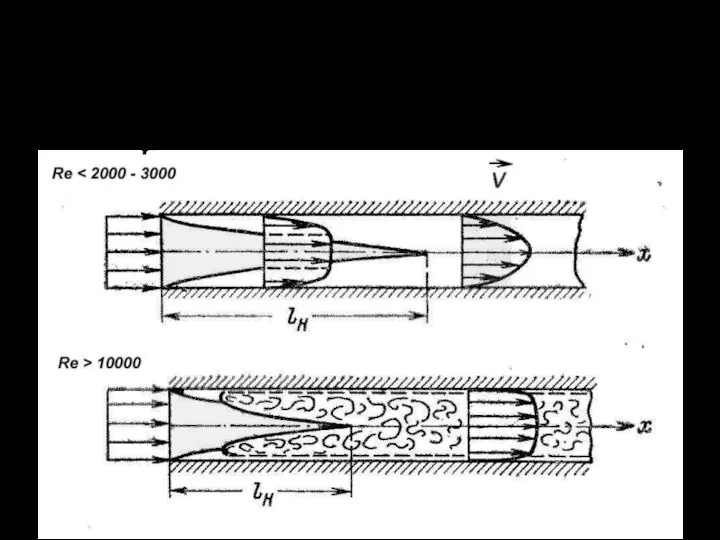 Установившееся течение газа через длинный трубопровод
Установившееся течение газа через длинный трубопровод Задача №16 Магнитная пушка
Задача №16 Магнитная пушка Движение материальной точки. Задачи
Движение материальной точки. Задачи Общий курс железных дорог. ОКЖД. Лекция 1
Общий курс железных дорог. ОКЖД. Лекция 1 Электромагнитное поле. Решение задач
Электромагнитное поле. Решение задач Реактивное движение
Реактивное движение Материалы для практических занятий экспертов по проверке и оценке заданий
Материалы для практических занятий экспертов по проверке и оценке заданий Электромагнитные колебания
Электромагнитные колебания Парообразование
Парообразование Дифференциальный подход
Дифференциальный подход Презентация на тему Телескоп
Презентация на тему Телескоп