Содержание
- 2. Определение силовых факторов с помощью линий влияния Определение с помощью линии влияния значения силового фактора от
- 3. ЗАГРУЖЕНИЕ ЛИНИЙ ВЛИЯНИЯ НЕПОДВИЖНЫМИ НАГРУЗКАМИ 1. Сосредоточенная нагрузка F F yF Л.В. S SF = F*
- 4. ЗАГРУЖЕНИЕ ЛИНИЙ ВЛИЯНИЯ НЕПОДВИЖНЫМИ НАГРУЗКАМИ 2. Сосредоточенный момент М F yF Л.В. S SM = M*
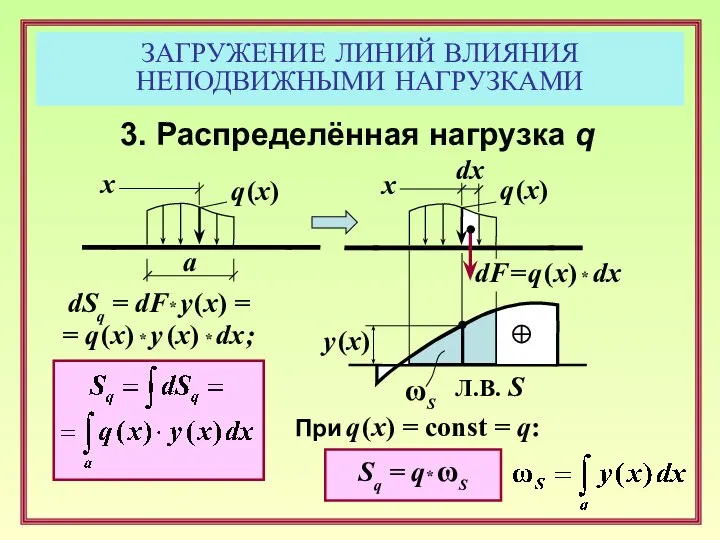
- 5. ЗАГРУЖЕНИЕ ЛИНИЙ ВЛИЯНИЯ НЕПОДВИЖНЫМИ НАГРУЗКАМИ y (x) Л.В. S Sq = q* ωS q (x) dx
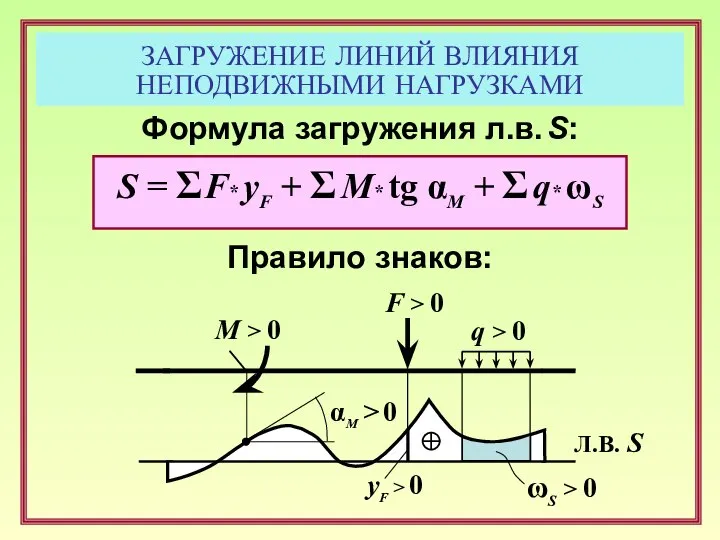
- 6. ЗАГРУЖЕНИЕ ЛИНИЙ ВЛИЯНИЯ НЕПОДВИЖНЫМИ НАГРУЗКАМИ Формула загружения л.в. S: Правило знаков: F > 0 yF >
- 7. ЗАГРУЖЕНИЕ ЛИНИЙ ВЛИЯНИЯ НЕПОДВИЖНЫМИ НАГРУЗКАМИ F1 y1 Л.В. S Использование статически эквивалентных преобразований нагрузок Статически эквивалентное
- 8. ЗАГРУЖЕНИЕ ЛИНИЙ ВЛИЯНИЯ НЕПОДВИЖНЫМИ НАГРУЗКАМИ F1 y1 Л.В. S Использование статически эквивалентных преобразований нагрузок Статически эквивалентное
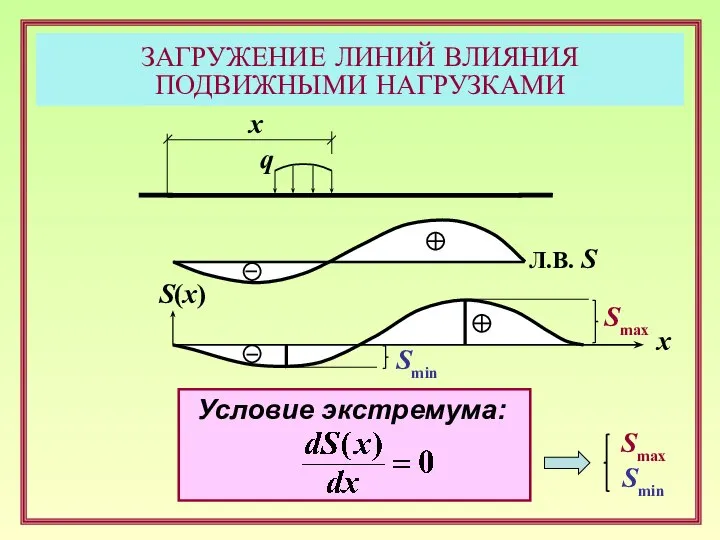
- 9. ЗАГРУЖЕНИЕ ЛИНИЙ ВЛИЯНИЯ ПОДВИЖНЫМИ НАГРУЗКАМИ q Л.В. S Smax x Условие экстремума: S(x) x Smin Smax
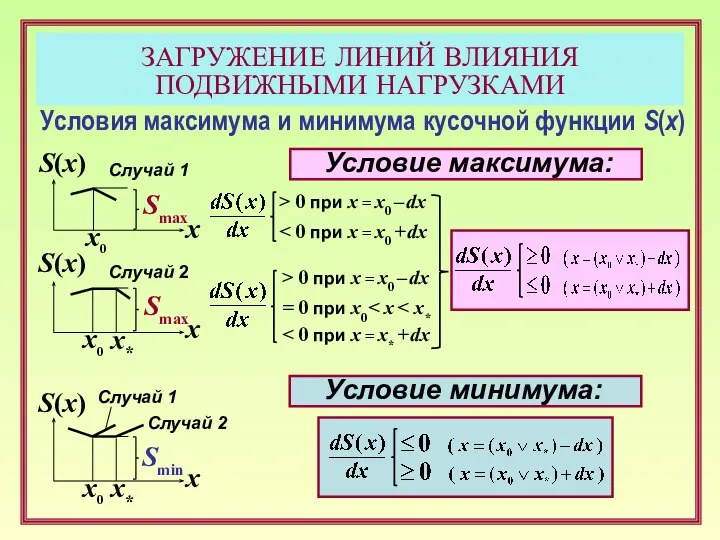
- 10. Smax Условие максимума: S(x) x Smin Условия максимума и минимума кусочной функции S(x) S(x) x Smax
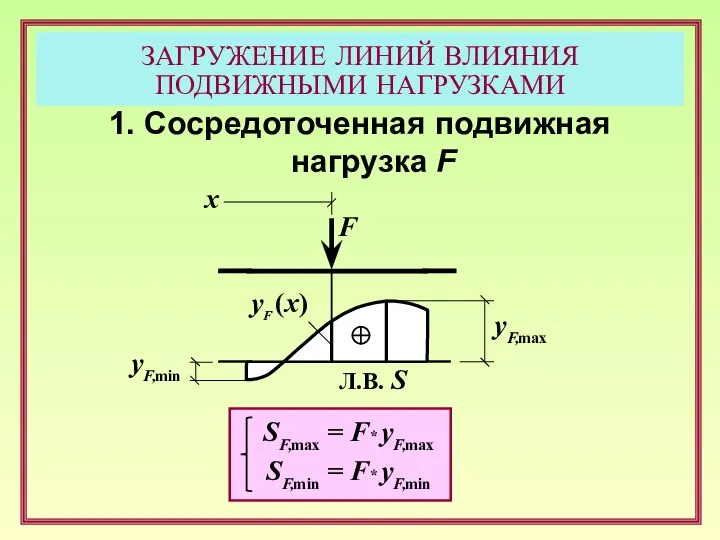
- 11. 1. Сосредоточенная подвижная нагрузка F F yF (x) Л.В. S yF,max yF,min x SF,max = F*
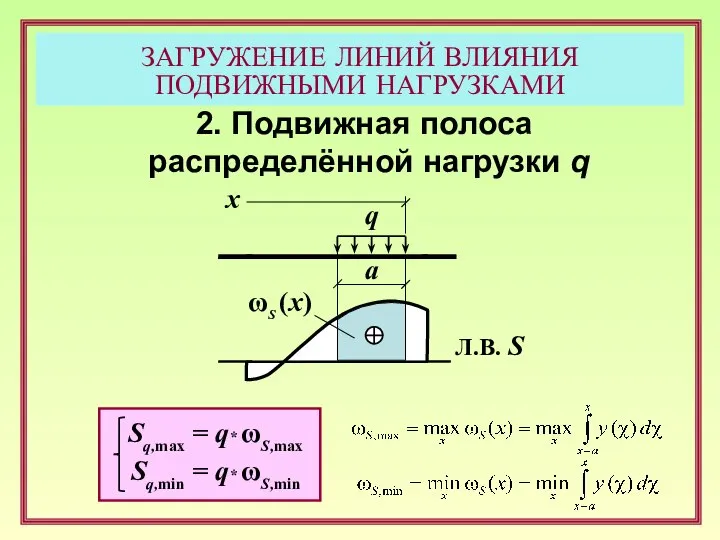
- 12. 2. Подвижная полоса распределённой нагрузки q q ωS (x) Л.В. S x а Sq,max = q*
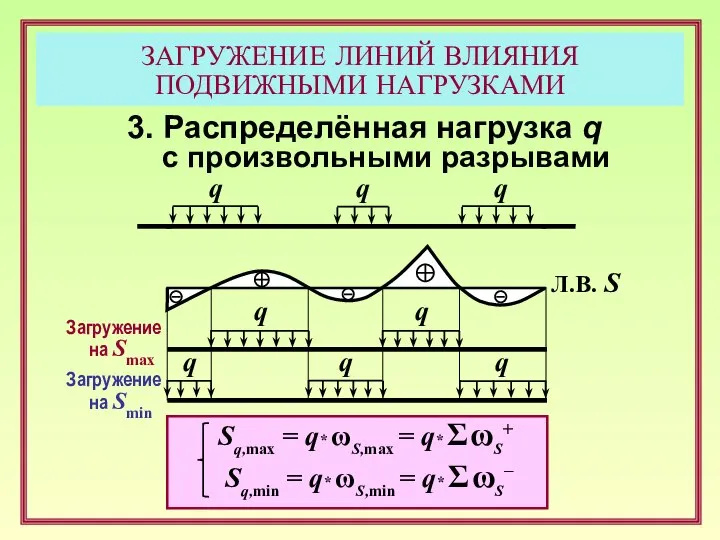
- 13. ЗАГРУЖЕНИЕ ЛИНИЙ ВЛИЯНИЯ ПОДВИЖНЫМИ НАГРУЗКАМИ 3. Распределённая нагрузка q с произвольными разрывами q Sq,max = q*
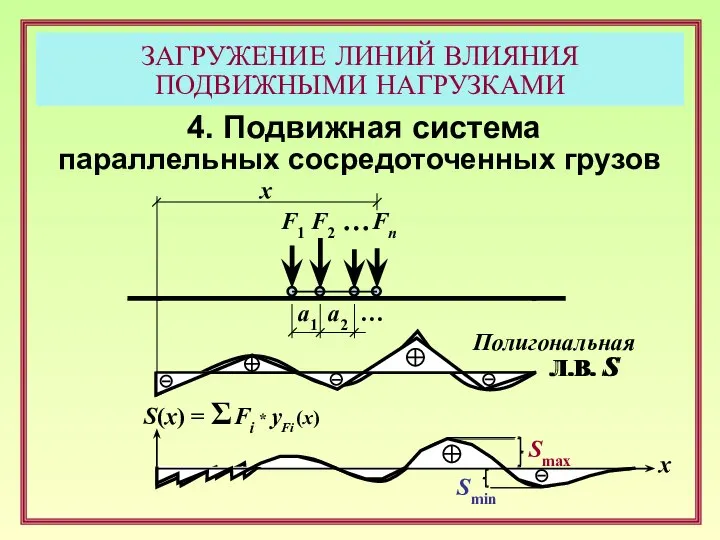
- 14. ЗАГРУЖЕНИЕ ЛИНИЙ ВЛИЯНИЯ ПОДВИЖНЫМИ НАГРУЗКАМИ 4. Подвижная система параллельных сосредоточенных грузов Л.В. S F1 F2 …
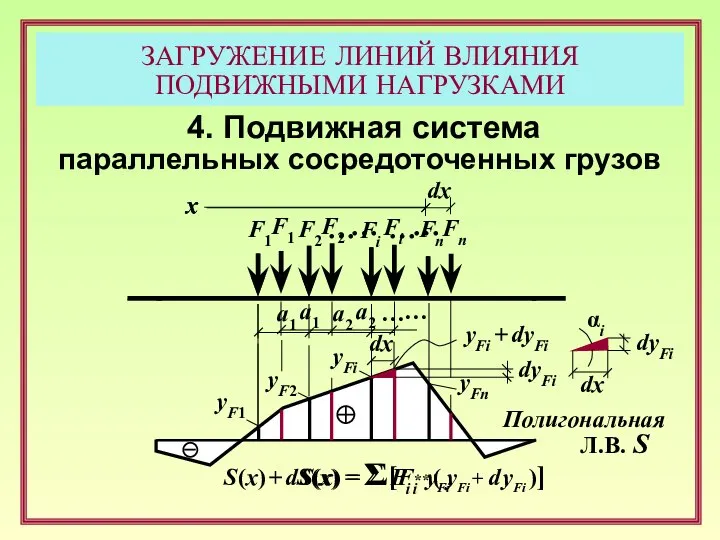
- 15. ЗАГРУЖЕНИЕ ЛИНИЙ ВЛИЯНИЯ ПОДВИЖНЫМИ НАГРУЗКАМИ 4. Подвижная система параллельных сосредоточенных грузов Полигональная Л.В. S F1 F2
- 16. ЗАГРУЖЕНИЕ ЛИНИЙ ВЛИЯНИЯ ПОДВИЖНЫМИ НАГРУЗКАМИ 4. Подвижная система параллельных сосредоточенных грузов dyFi dx αi Σ Fi
- 17. ЗАГРУЖЕНИЕ ЛИНИЙ ВЛИЯНИЯ ПОДВИЖНЫМИ НАГРУЗКАМИ 4. Подвижная система параллельных сосредоточенных грузов Полигональная Л.В. S F1 F2
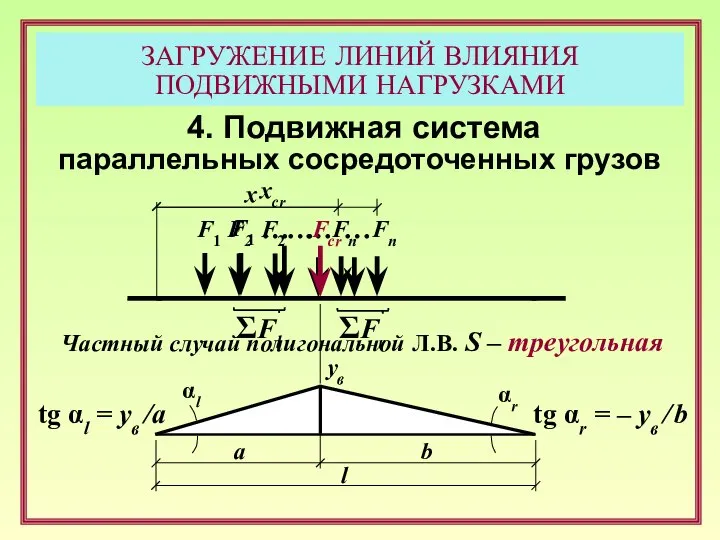
- 18. ЗАГРУЖЕНИЕ ЛИНИЙ ВЛИЯНИЯ ПОДВИЖНЫМИ НАГРУЗКАМИ 4. Подвижная система параллельных сосредоточенных грузов Частный случай полигональной Л.В. S
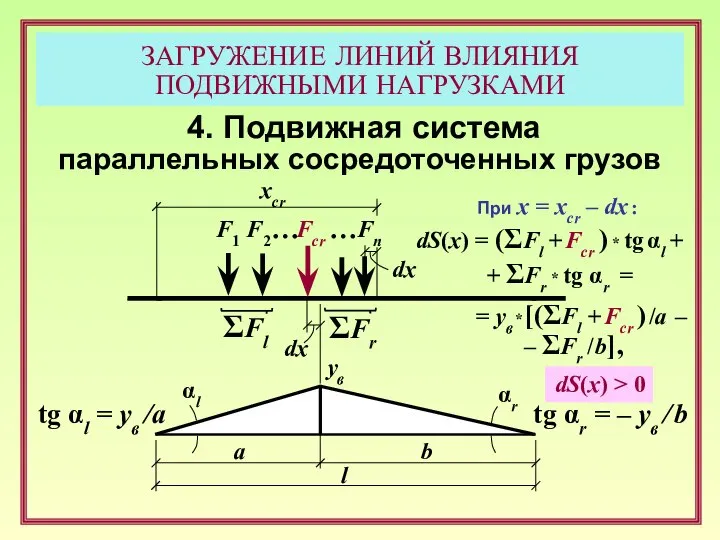
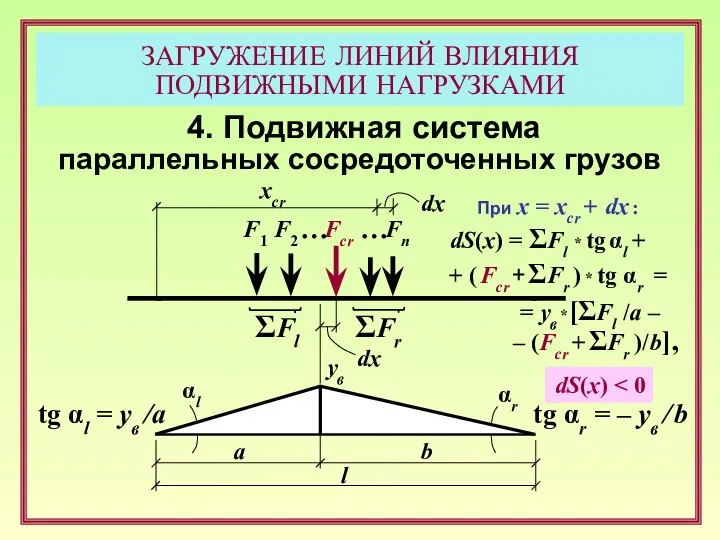
- 19. ЗАГРУЖЕНИЕ ЛИНИЙ ВЛИЯНИЯ ПОДВИЖНЫМИ НАГРУЗКАМИ 4. Подвижная система параллельных сосредоточенных грузов F1 F2 … Fn a
- 20. ЗАГРУЖЕНИЕ ЛИНИЙ ВЛИЯНИЯ ПОДВИЖНЫМИ НАГРУЗКАМИ 4. Подвижная система параллельных сосредоточенных грузов F1 F2 … Fn a
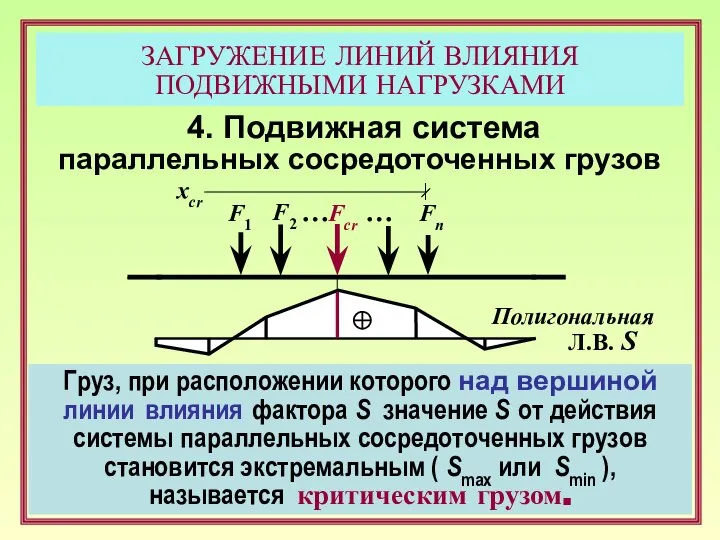
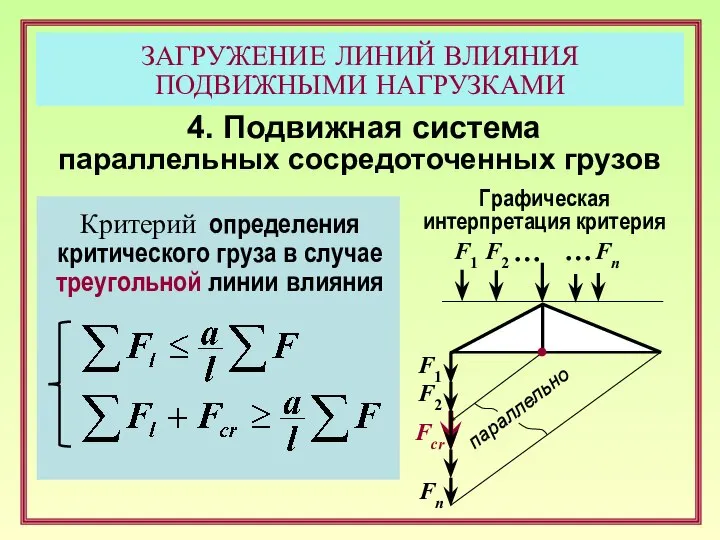
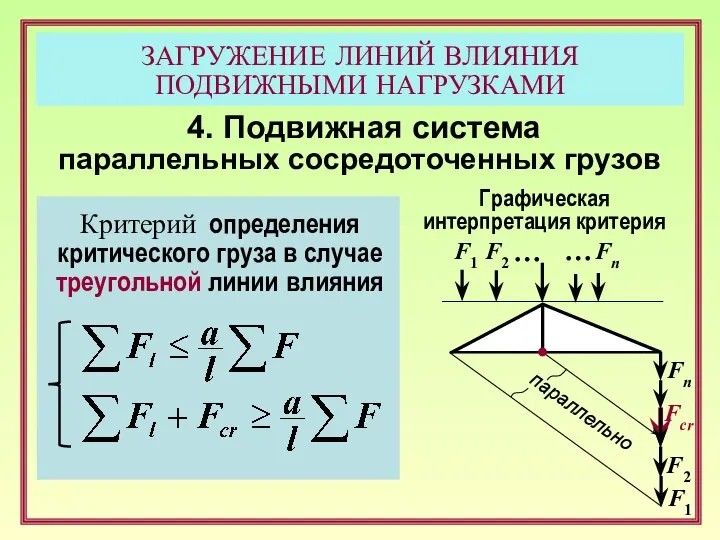
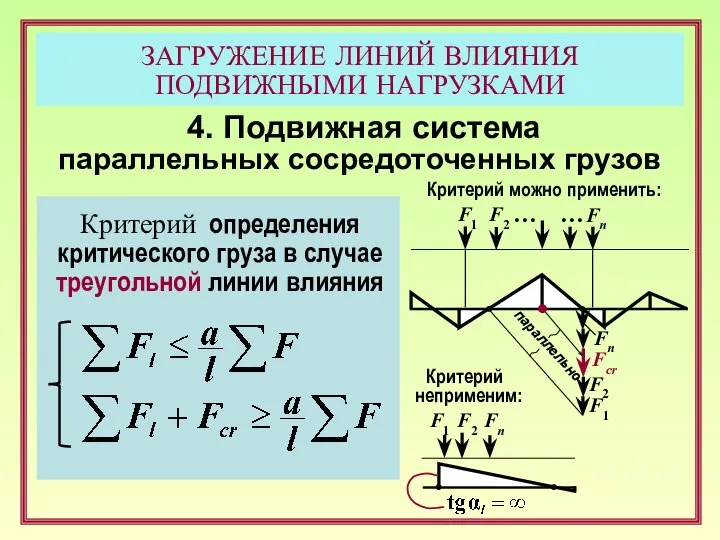
- 21. ЗАГРУЖЕНИЕ ЛИНИЙ ВЛИЯНИЯ ПОДВИЖНЫМИ НАГРУЗКАМИ 4. Подвижная система параллельных сосредоточенных грузов Критерий определения критического груза в
- 22. ЗАГРУЖЕНИЕ ЛИНИЙ ВЛИЯНИЯ ПОДВИЖНЫМИ НАГРУЗКАМИ 4. Подвижная система параллельных сосредоточенных грузов Критерий определения критического груза в
- 23. ЗАГРУЖЕНИЕ ЛИНИЙ ВЛИЯНИЯ ПОДВИЖНЫМИ НАГРУЗКАМИ 4. Подвижная система параллельных сосредоточенных грузов Критерий определения критического груза в
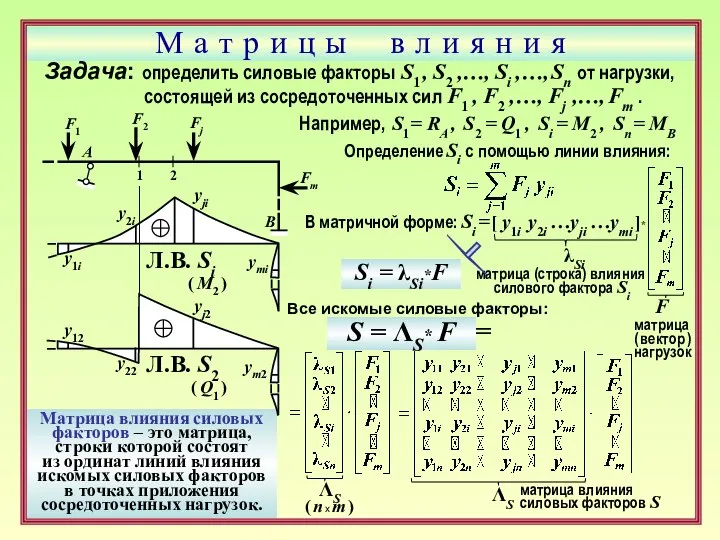
- 24. М а т р и ц ы в л и я н и я Задача: определить
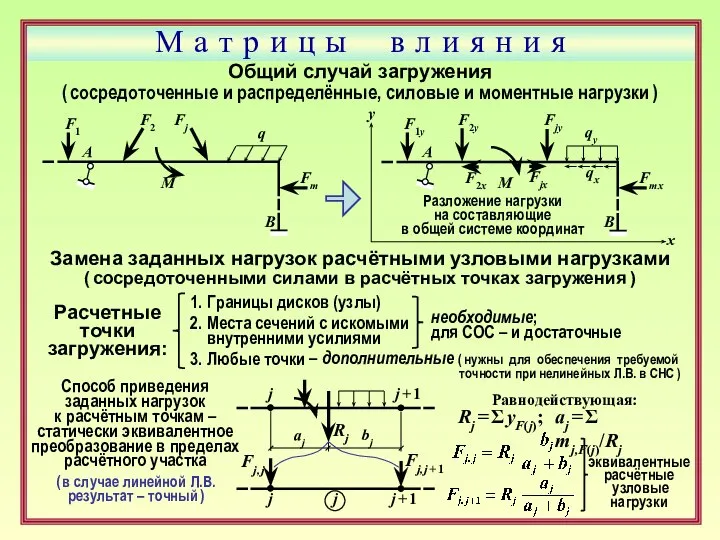
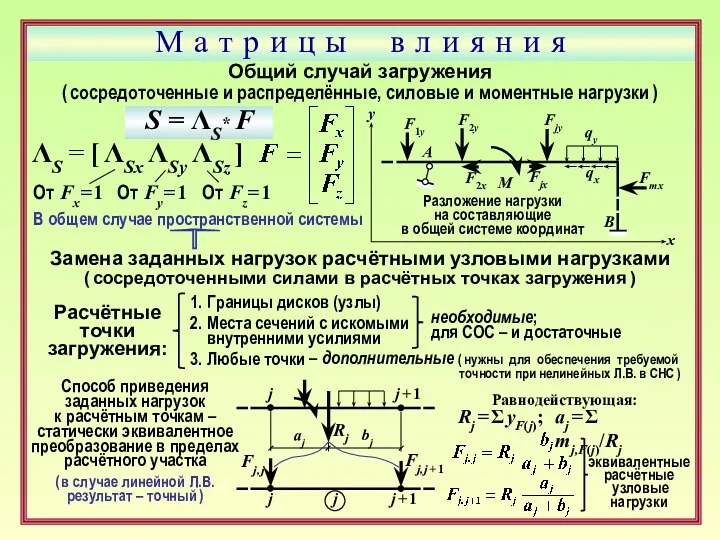
- 25. М а т р и ц ы в л и я н и я Общий случай
- 26. М а т р и ц ы в л и я н и я Общий случай
- 27. М а т р и ц ы в л и я н и я Замена заданных
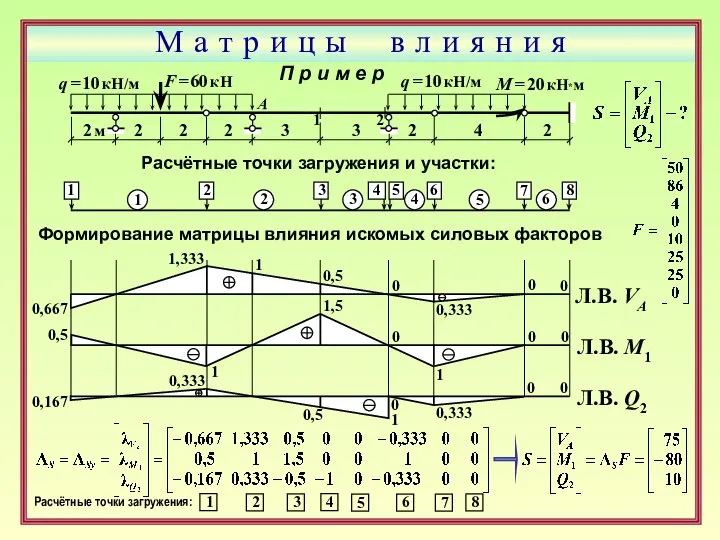
- 28. М а т р и ц ы в л и я н и я Формирование матрицы
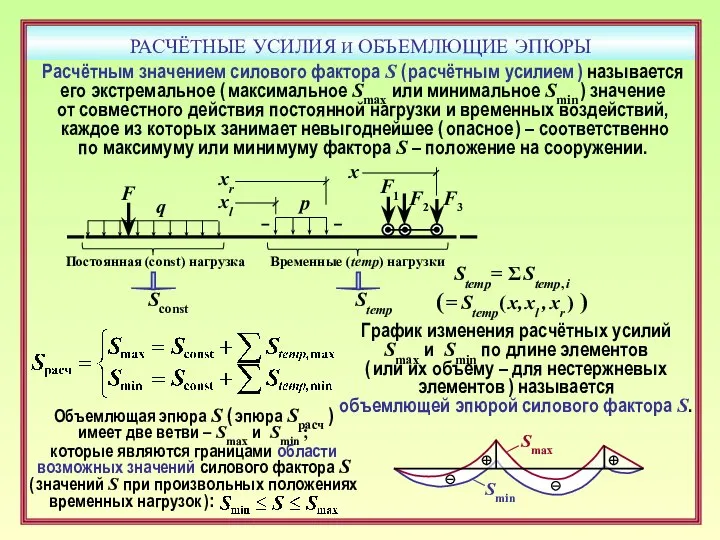
- 29. РАСЧЁТНЫЕ УСИЛИЯ И ОБЪЕМЛЮЩИЕ ЭПЮРЫ F Расчётным значением силового фактора S ( расчётным усилием ) называется
- 30. РАСЧЁТНЫЕ УСИЛИЯ И ОБЪЕМЛЮЩИЕ ЭПЮРЫ Расчётным значением силового фактора S ( расчётным усилием ) называется его
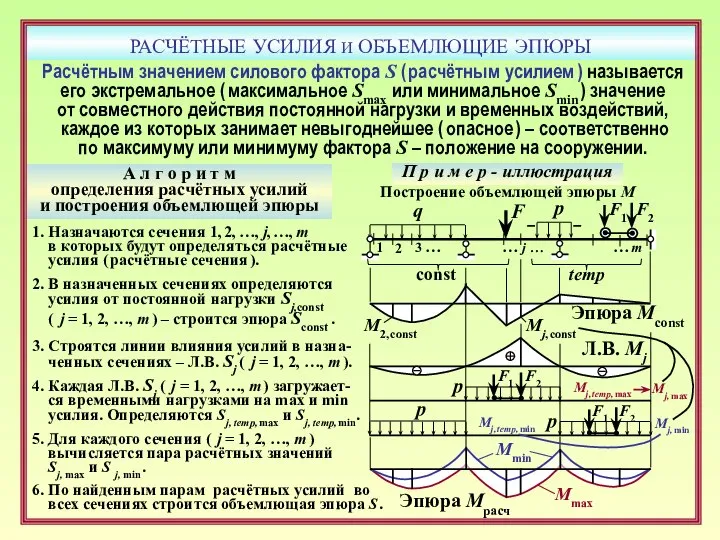
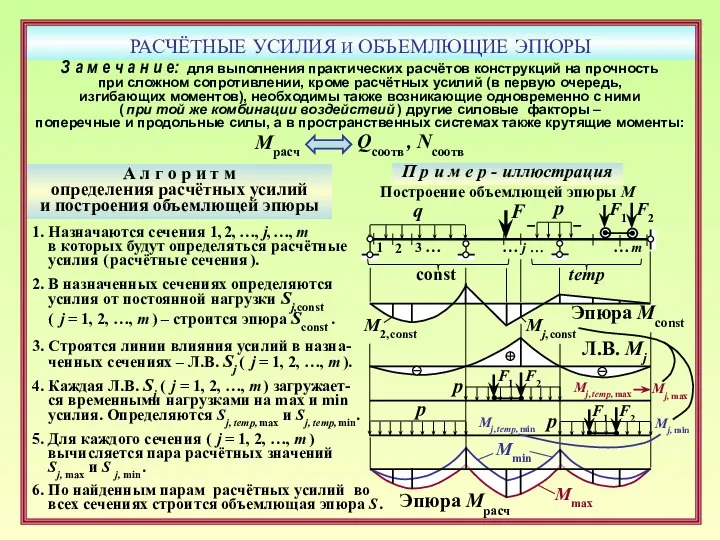
- 31. РАСЧЁТНЫЕ УСИЛИЯ И ОБЪЕМЛЮЩИЕ ЭПЮРЫ Mmax Mmin А л г о р и т м определения
- 32. К о н т р о л ь н ы е в о п р о
- 34. Скачать презентацию








 Магнитное поле. Примеры магнитных полей
Магнитное поле. Примеры магнитных полей Примеры решения задач на цепи с взаимной индукцией
Примеры решения задач на цепи с взаимной индукцией Магнитное поле тока
Магнитное поле тока Электрический заряд
Электрический заряд Электрическое поле. Тест. 10 класс
Электрическое поле. Тест. 10 класс Вращение шестеренки
Вращение шестеренки Презентация _Механические передачи. 5 класс_
Презентация _Механические передачи. 5 класс_ О времени и пространстве
О времени и пространстве Расчет и выбор посадок подшипников качения на валы и в отверстия корпусов
Расчет и выбор посадок подшипников качения на валы и в отверстия корпусов 2_kurs_lektsia_1_2
2_kurs_lektsia_1_2 Основы электричества. Электрическая цепь
Основы электричества. Электрическая цепь OVZ_L2_L3 (2)
OVZ_L2_L3 (2) Презентация на тему Энергосбережение в быту (8 класс)
Презентация на тему Энергосбережение в быту (8 класс)  Методы и приборы для измерения влажности газовых сред
Методы и приборы для измерения влажности газовых сред Волновая оптика
Волновая оптика Измерение мощности и работы тока в электрической лампе. Лабораторная работа
Измерение мощности и работы тока в электрической лампе. Лабораторная работа Средства измерений и их основные элементы
Средства измерений и их основные элементы Беседа Понятие об источниках тока
Беседа Понятие об источниках тока Сельскохозяйственные машины
Сельскохозяйственные машины Электрические силы
Электрические силы Движение небесных тел под действием сил тяготения
Движение небесных тел под действием сил тяготения Расчет силы тока и напряжения в электрических цепях
Расчет силы тока и напряжения в электрических цепях Формирование и развитие физических понятий
Формирование и развитие физических понятий Давление твёрдых тел, жидкостей и газов
Давление твёрдых тел, жидкостей и газов Устройство, с помощью которого человек выполняет физическую работу, или подвижная часть более сложного устройства
Устройство, с помощью которого человек выполняет физическую работу, или подвижная часть более сложного устройства Амплитудная цилиндрическая дифракционная линза. Расчет, изготовление с помощью фотолитографии и жидкостного травления
Амплитудная цилиндрическая дифракционная линза. Расчет, изготовление с помощью фотолитографии и жидкостного травления Дефекты и наноструктурные материалы
Дефекты и наноструктурные материалы Презентация на тему Оптические явления в атмосфере
Презентация на тему Оптические явления в атмосфере