Содержание
- 2. Оглавление Кинематика точки. Дифференцирование вектора постоянного модуля…………………………………………………………………………….……………………..3 Кинематика точки в декартовой системе координат.……………………………………………………………………………………………...9 Кинематика точки в
- 3. Понятие вектора и производной Рис. 1.1.1 Графическое изображение вектора и его обозначение
- 4. Вектор-функции
- 5. Пространственная линия – годограф радиуса-вектора Рис. 1.1.2 Пример вектор-функций (вверху слева) и изображений годографа
- 6. Геометрический и физический смысл Рис. 1.1.3 К геометрическому смыслу производной S M y x z
- 7. Рис. 1.1.4
- 9. Материальная точка – идеализированная физическая модель, обладающее массой тело, размерами, формой, вращением и внутренней структурой которого
- 10. Кинематика в ДСК Рис. 1.2.3
- 11. Формулы скорости и ускорения в ДСК Рис. 1.2.4
- 12. Выводы Иногда производить описание движения тела проще в декартовых координатах. Таким образом, мы получаем удобный аппарат
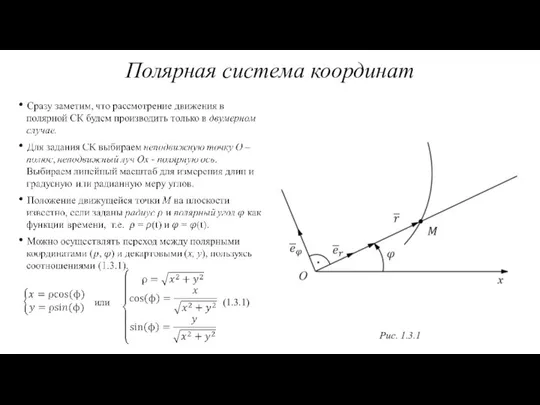
- 13. Полярная система координат Рис. 1.3.1 или (1.3.1)
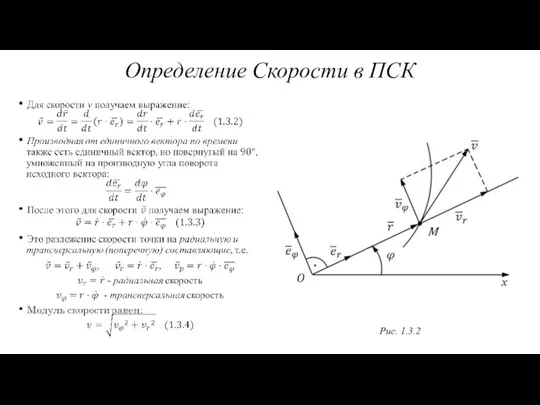
- 14. Рис. 1.3.2 Определение Скорости в ПСК
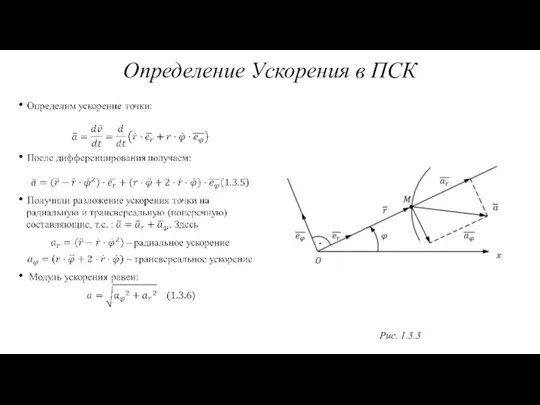
- 15. Определение Ускорения в ПСК Рис. 1.3.3
- 16. Для определения закона движения точки в естественной системе координат нам необходимо: Знать траекторию движения точки Установить
- 17. Касательная, главная нормаль и радиус кривизны
- 18. Кривизна и радиус кривизны плоской кривой
- 19. Определение скорости и ускорения Рис. 1.4.3
- 20. Определение скорости и ускорения Рис. 1.4.4
- 21. Определение сложного движения Рис. 1.5.1
- 22. Движение точки M по отношению к неподвижной системе отсчета – абсолютное движение. Её скорость и ускорение
- 23. Теорема о сложении скоростей Рис. 1.5.2
- 24. Теорема о сложении скоростей
- 25. Рис. 1.5.3 Теорема о сложении ускорений
- 26. Теорема о сложении ускорений
- 27. Твёрдое тело (ТТ) – система материальных точек. Абсолютно твёрдое тело – идеализированная механическая система материальных точек,
- 28. Рис. 2.1.1 К доказательству основной теоремы кинематики ТТ Основная теорема кинематики твёрдого тела
- 29. Поступательное движение ТТ – такое движение твердого тела, при котором любая прямая, проведенная в этом теле,
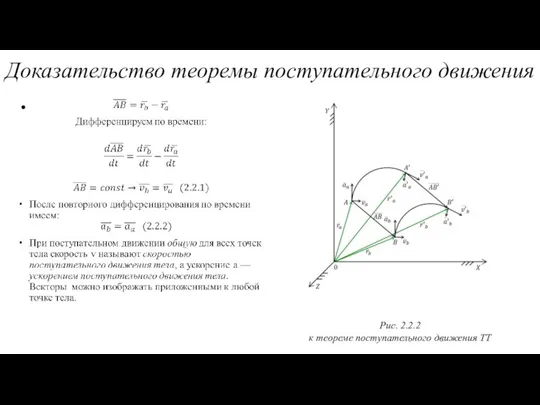
- 30. Рис. 2.2.2 к теореме поступательного движения ТТ Доказательство теоремы поступательного движения
- 31. Вращение твердого тела вокруг неподвижной оси
- 32. Рис. 2.3.1 вращательное движение тела Вращение твердого тела вокруг неподвижной оси
- 33. Рис. 2.3.2 к определению направления углового ускорения (вращение вокруг неподвижной оси) Вращение твердого тела вокруг неподвижной
- 34. Рис. 2.3.3 Кинематика точки ТТ в ЕСК Вращение твердого тела вокруг неподвижной оси
- 35. Рис. 2.3.4 к векторному представлению кинематических характеристик точки ТТ Вращение твердого тела вокруг неподвижной оси
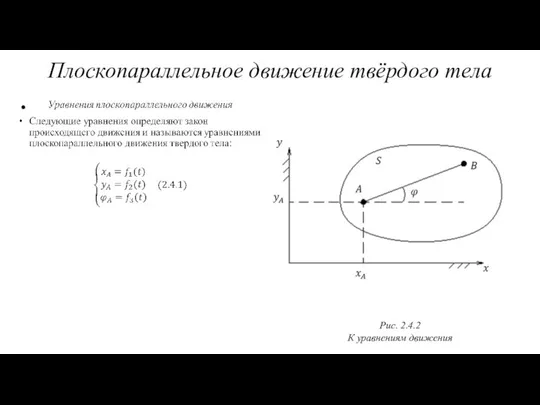
- 36. Определение Плоскопараллельным (или просто плоским) движением твёрдого тела называют такое движение, при котором все точки перемещаются
- 37. Рис. 2.4.2 К уравнениям движения Плоскопараллельное движение твёрдого тела
- 38. Рис. 2.4.3 Плоское движение как сумма поступательного и вращательного Плоскопараллельное движение твёрдого тела
- 39. Рис. 2.4.4 К кинематике плоского движения Плоскопараллельное движение твёрдого тела
- 40. Рис. 2.4.5 К теореме о представлении скоростей Плоскопараллельное движение твёрдого тела
- 41. Плоскопараллельное движение твёрдого тела
- 42. Мгновенный центр скоростей Рис. 2.4.6
- 43. Мгновенный центр ускорений Так, ускорение любой точки тела есть векторная сумма ускорения полюса и ускорения точки
- 44. Мгновенный центр ускорений Рис. 2.4.7 Мгновенный центр ускорений
- 45. Основные понятия ТММ Теория механизмов и машин занимается созданием и изучением высокопроизводительных механизмов и машин. Механизм
- 46. Разновидности звеньев Звено – либо одна деталь, либо совокупность нескольких деталей, соединенных в одну кинематически неизменяемую
- 47. Кинематические пары и цепи Кинематическая пара – подвижное соединение звеньев, допускающее их относительное движение. Все кинематические
- 48. Классификация кинематических пар
- 49. Классификация кинематических пар (продолжение) Цилиндрическая пара (рис. 2.5.3, в) – двухподвижная (2 ц), низшая, допускает независимые
- 50. Классификация кинематических пар (продолжение) Таблица 2.5.1 Классификация кинематических пар
- 51. Степень подвижности Таблица 2.5.2 Классификация кинематических пар по числу степеней свободы и числу связей
- 52. Степень подвижности плоского механизма
- 53. Степень подвижности плоского механизма
- 54. Структурные группы Ассура
- 55. Классификация структурных групп Конечные звенья групп Ассура, входящие в две кинематические пары, из которых одна имеет
- 56. Структурный анализ с помощью СГ Рис. 2.6.2
- 57. Структурные формулы механизмов После отсоединения от механизма всех структурных групп останется стойка и начальные звенья, число
- 58. Структурный синтез по Ассуру Рис. 2.6.4
- 59. ДЗ №1
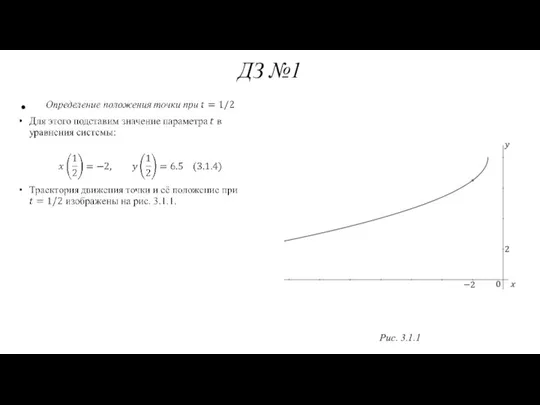
- 60. ДЗ №1 Рис. 3.1.1
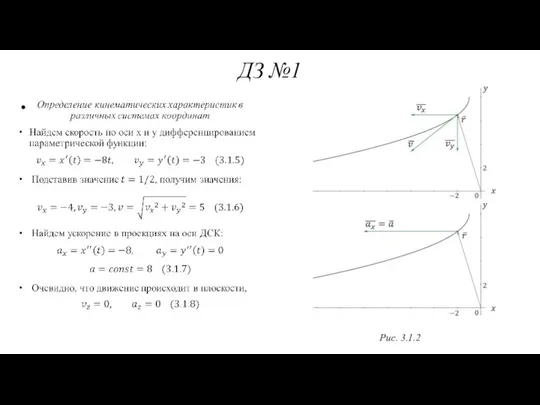
- 61. ДЗ №1 Рис. 3.1.2
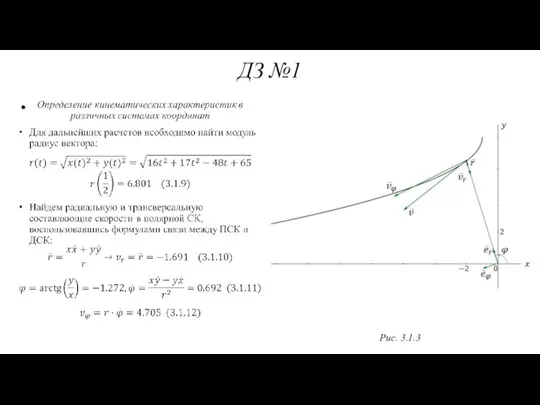
- 62. ДЗ №1 Рис. 3.1.3
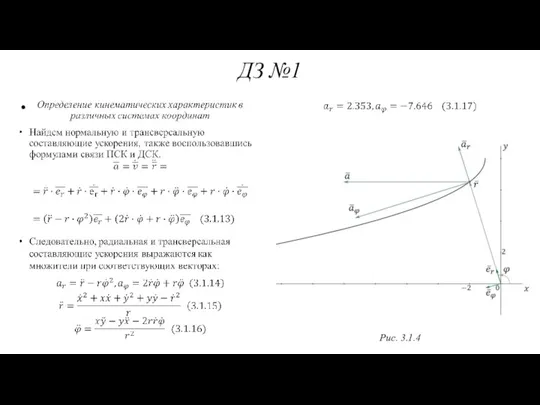
- 63. ДЗ №1 Рис. 3.1.4
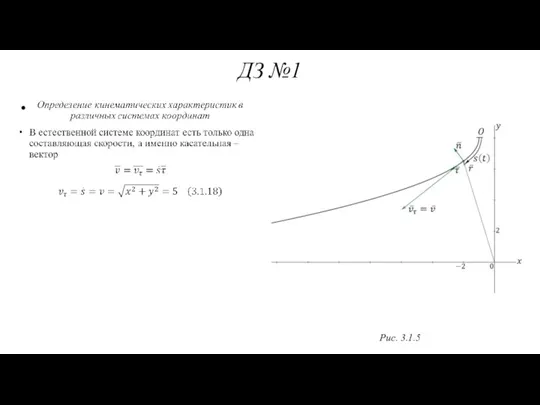
- 64. ДЗ №1 Рис. 3.1.5
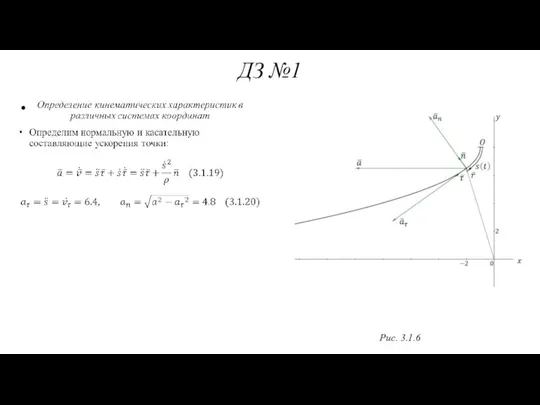
- 65. ДЗ №1 Рис. 3.1.6
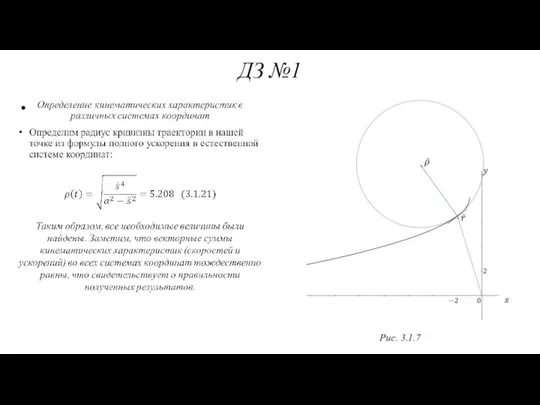
- 66. ДЗ №1 Рис. 3.1.7
- 67. ДЗ №2 Для данного механизма: Определить число звеньев и кинематических пар. Указать виды абсолютных движений, совершаемых
- 68. ДЗ №2 (1) Число звеньев имеющегося механизма – 4 (включая стойку), а именно: Коромысло 1 Шатун
- 69. ДЗ №2 (2,3) Траектории характерных точек: A – неподвижная. B – окружность. C – прямая. D
- 70. ДЗ №2 (4,5) Представленный механизм может производить различную работу по превращению движения в зависимости от выбора
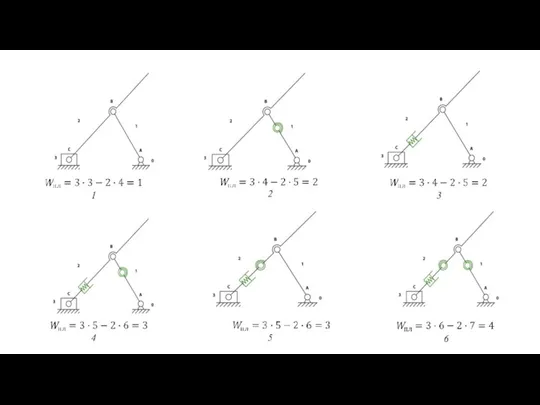
- 71. ДЗ №3 Требуется определить виды напряженно-деформированных состояний звеньев и рассмотреть все возможные их комбинации. Заметим, что
- 72. 1 2 3 4 5 6
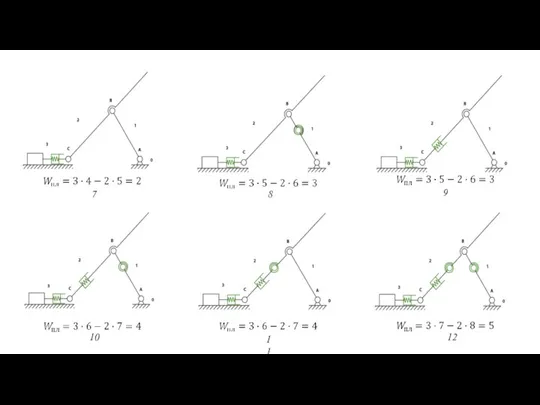
- 73. 7 8 9 10 11 12
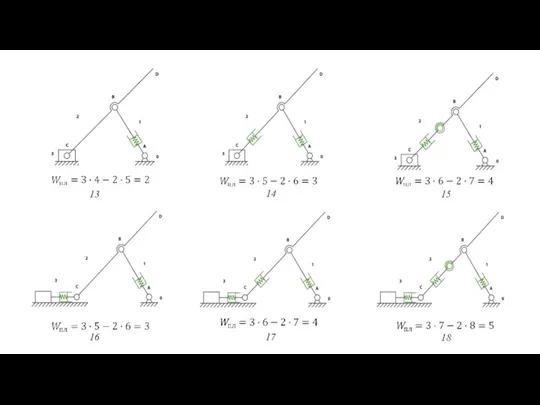
- 74. 13 14 15 16 17 18
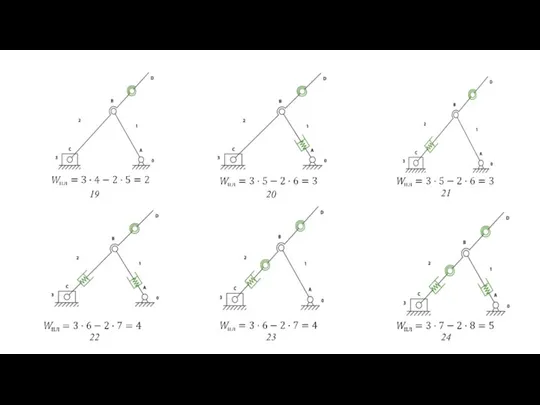
- 75. 19 20 21 22 23 24
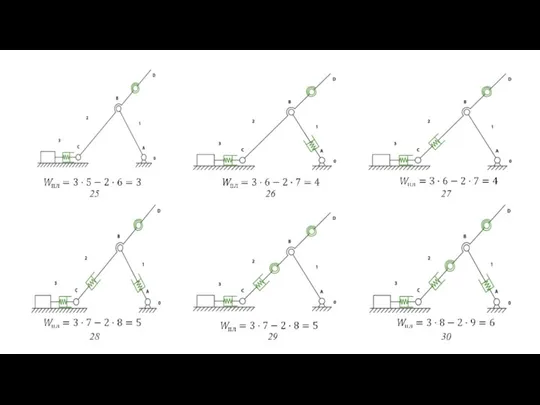
- 76. 25 26 27 28 29 30
- 77. ДЗ №3 Рис. 3.3.31 Эскиз с примерной формой звеньев для наиболее сложной конфигурации их НДС
- 79. Скачать презентацию



























































 Получение нанокапель методом сверхзвукового разшерения
Получение нанокапель методом сверхзвукового разшерения 0 гениальных изобретений Николы Тесла
0 гениальных изобретений Николы Тесла Оптика
Оптика Методы повышения конструкционной прочности деталей машин
Методы повышения конструкционной прочности деталей машин Конденсатор. Индуктивность
Конденсатор. Индуктивность Перенос графена на произвольную подложку
Перенос графена на произвольную подложку Характеристика волн
Характеристика волн Движение по окружности
Движение по окружности Сила тяжести на других планетах. Урок 27
Сила тяжести на других планетах. Урок 27 Открытие фотоэффекта
Открытие фотоэффекта Условие передачи максимума средней мощности от источника к приемнику
Условие передачи максимума средней мощности от источника к приемнику Законы геометрической оптики
Законы геометрической оптики Случайные фракталы
Случайные фракталы Применение первого закона термодинамики к изопроцессам. 10 класс
Применение первого закона термодинамики к изопроцессам. 10 класс Первый пароход 4/2 класс
Первый пароход 4/2 класс Физико-химический марафон
Физико-химический марафон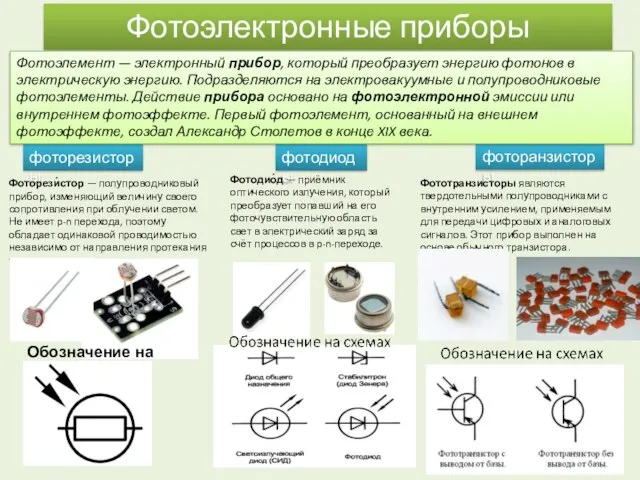 Фотоэлектронные приборы
Фотоэлектронные приборы Электромагнитная индукция
Электромагнитная индукция Познавательная игра для учащихся 9 класса Макова Л.И. МОУ Есиповская сош
Познавательная игра для учащихся 9 класса Макова Л.И. МОУ Есиповская сош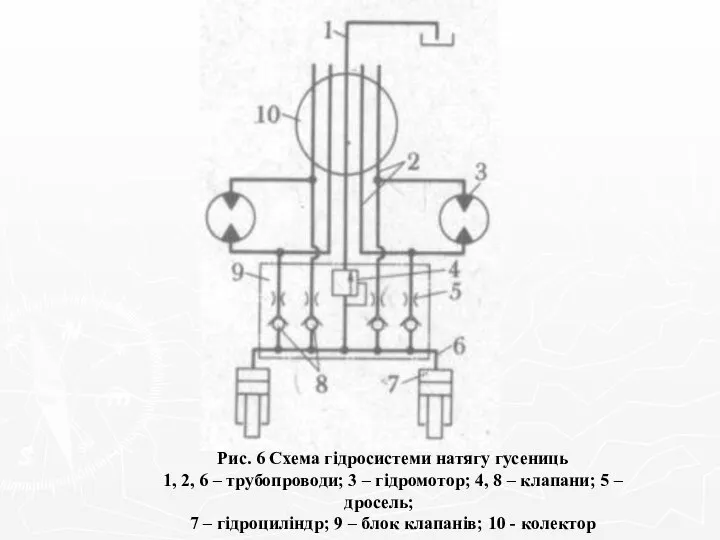 Схема гідросистеми натягу гусениць
Схема гідросистеми натягу гусениць методичка1 - Расчет тайминга движущихся предметов
методичка1 - Расчет тайминга движущихся предметов Метод переходного состояния. Классическая теория
Метод переходного состояния. Классическая теория Судостроение. Что общего у предметов?
Судостроение. Что общего у предметов? Количество вщства. Решение задач
Количество вщства. Решение задач Теория вероятностей в задачах ЕГЭ
Теория вероятностей в задачах ЕГЭ Решение задач
Решение задач Механическое движение
Механическое движение Обратимые и необратимые процессы. Энтропия. Второй закон термодинамики
Обратимые и необратимые процессы. Энтропия. Второй закон термодинамики