Слайд 2Условия обучения
По итогам изучения дисциплины проводится экзамен
В течение семестра необходимо выполнить все

задания по календарному плану, который опубликован на Учебном портале
Для допуска на сессию набрать 40 баллов
Слайд 3Список литературы
1. Бесекерский В.Л., Попов Е.П. Теория систем автоматического управления. СПб.: Профессия,

2003.
2. Теория автоматического управления. Ч. 1 Теория линейных систем автоматического управления / под ред. Академика А.А.Воронова. 2-е изд. М.: Высшая школа, 1984.
3. Босс В. Лекции по теории управления. Т.1: Автоматическое регулирование. М.: ЛЕНАНД, 2017
4. Рощин А.В. Основы теории автоматического управления. Учебное пособие. М.: МГУПИ, 2007
Слайд 4Темы дисциплины
Управление и информатика, построение модели простого объекта, общие принципы системной организации,

построение передаточной функции, формы представления моделей, инвариантность и чувствительность систем управления, уравнения в нормальной форме, задача Коши, передаточная матрица. Математические модели объектов и систем управления, переходные и частотные характеристики объекта, весовая функция, переходная функция, частотные характеристики, логарифмические частотные характеристики, асимптотические логарифмические частотные характеристики.
Слайд 5Темы дисциплины
Проблема устойчивости, типовые элементарные звенья, интегрирующее звено, апериодическое звено, колебательное звено,

дифференцирующее звено, соединение звеньев. Исследование системы автоматического управления. построение логарифмических частотных характеристик, проверка устойчивости системы, запас устойчивости по фаз, запас устойчивости по амплитуде.
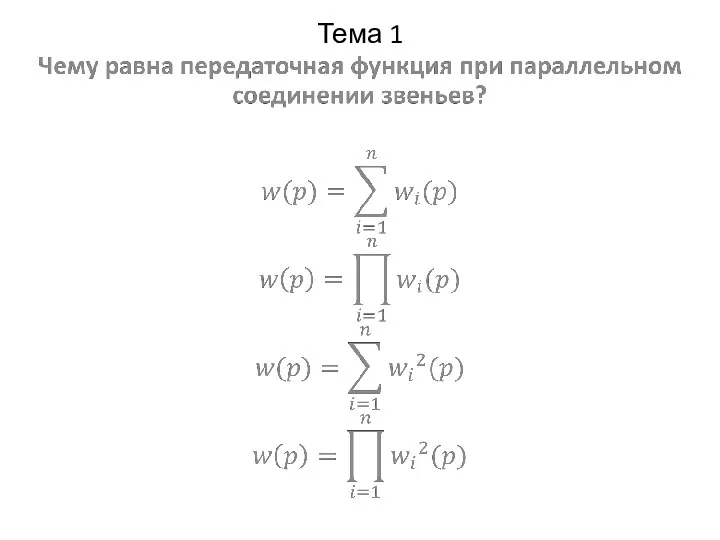
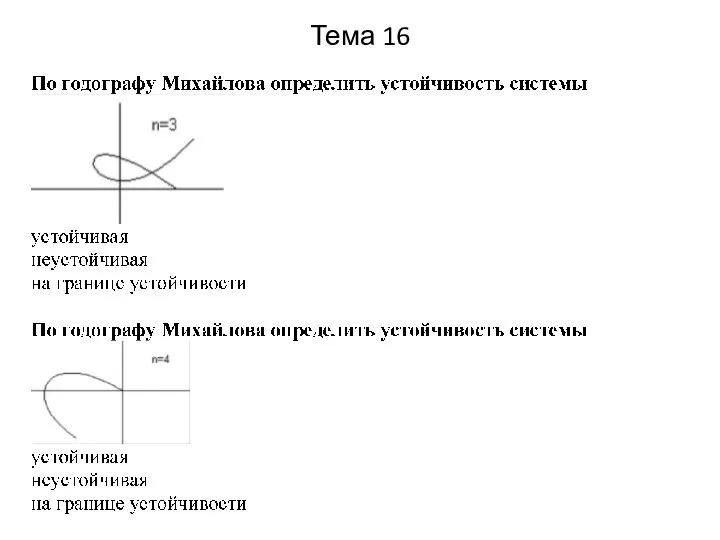
Слайд 12Тема 2
При описании объекта управления в непрерывной модели общего вида вектор-функция обозначается

буквой
х
u
f
q
w
z
При описании объекта управления в непрерывной модели общего вида вектор наблюдения обозначается буквой
х
u
f
q
w
z
При описании объекта управления в непрерывной модели общего вида вектор помехи измерения обозначается буквой
u
v
f
q
w
z
При описании объекта управления в непрерывной модели общего вида вектор состояния обозначается буквой
х
u
f
q
w
z
Слайд 13Тема 2
При описании объекта управления в непрерывной модели общего вида вектор параметров

обозначается буквой
х
u
f
q
w
z
При описании объекта управления в непрерывной модели общего вида вектор случайных возмущений обозначается буквой
х
u
f
q
w
z
При описании объекта управления в непрерывной модели общего вида вектор параметров обозначается буквой
х
u
f
q
w
z
Слайд 16Тема 3
Главным признаком задачи Коши является задание граничных условий на переменные
в

одной точке (в конце интервала).
в одной точке (в начале интервала)
в одной точке (не принципиально, в конце или в начале интервала)
в двух точках
в трех точках
в нескольких точках
Задача называется многоточечной граничной, или просто граничной,
если граничные условия для разных координат вектора состояния задаются:
в одной точке (в конце интервала).
в одной точке (в начале интервала)
в одной точке (не принципиально, в конце или в начале интервала)
в двух точках
в трех точках
в нескольких точках
Слайд 17Тема 3
В решении в форме Коши
свободное движение задано выражением:
В решении

в форме Коши
вынужденное движение задано выражением:
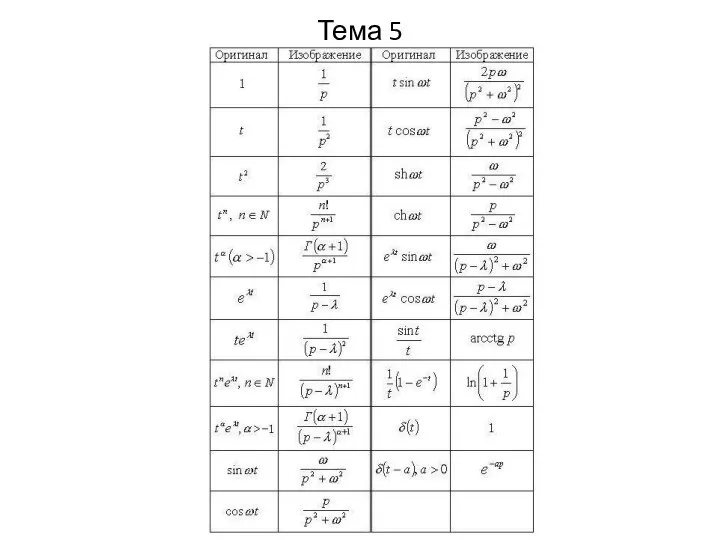
Слайд 22Тема 5
Чему равна весовая функция апериодического звена?

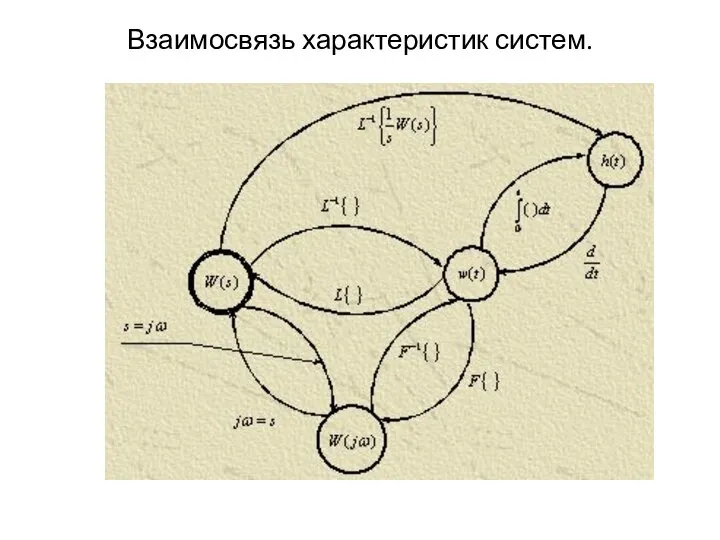
Слайд 57Взаимосвязь характеристик систем.





















































 Магнитное взаимодействие. Искусственные и естественные магниты
Магнитное взаимодействие. Искусственные и естественные магниты Законы проведения возбуждения по нервному волокну. Парабиоз. Физиологические свойства синапсов
Законы проведения возбуждения по нервному волокну. Парабиоз. Физиологические свойства синапсов Kinematika_tverdogo_tela_33__33__33
Kinematika_tverdogo_tela_33__33__33 Законы сохранения
Законы сохранения Свободное падение тел. Движение точки по окружности
Свободное падение тел. Движение точки по окружности ВКР: совершенствование сервисного обслуживания с модернизацией стенда для проверки форсунок грузовых автомобилей
ВКР: совершенствование сервисного обслуживания с модернизацией стенда для проверки форсунок грузовых автомобилей Зарядные машины для подземных работ
Зарядные машины для подземных работ ВСР №15. Голография и ее применение
ВСР №15. Голография и ее применение Закон сохранения полной механической энергии
Закон сохранения полной механической энергии СИЛА ТРЕНИЯ, ЕЕ РОЛЬ В ПРИРОДЕ, ТЕХНИКЕ И ПОВСЕДНЕВНОЙ ЖИЗНИ. Выполнил: Кишко А. 7 класс МКОУ Атамановской СОШ Учитель: Янюшкина
СИЛА ТРЕНИЯ, ЕЕ РОЛЬ В ПРИРОДЕ, ТЕХНИКЕ И ПОВСЕДНЕВНОЙ ЖИЗНИ. Выполнил: Кишко А. 7 класс МКОУ Атамановской СОШ Учитель: Янюшкина  Оптические игрушки
Оптические игрушки Спектры и спектральный анализ
Спектры и спектральный анализ Прямоугольная яма
Прямоугольная яма Потужність
Потужність Тепловая генерация энергии на основе холодного ядерного синтеза
Тепловая генерация энергии на основе холодного ядерного синтеза Уравнение состояния идеального газа
Уравнение состояния идеального газа Электромагнетический индукционный генератор-устройство
Электромагнетический индукционный генератор-устройство Mekhanizm_gazoraspredelenia
Mekhanizm_gazoraspredelenia Механический ткацкий станок
Механический ткацкий станок Магнитное_поле_в_вакууме
Магнитное_поле_в_вакууме Технологические характеристики грунтов. Определение трудности процессов разработки горных пород
Технологические характеристики грунтов. Определение трудности процессов разработки горных пород Презентация на тему Правило Ленца. Явление самоиндукции
Презентация на тему Правило Ленца. Явление самоиндукции  МотоСкороХоды
МотоСкороХоды Закон сохранения импульса
Закон сохранения импульса Презентация на тему Сила упрогости
Презентация на тему Сила упрогости  impuls_prezentatsia
impuls_prezentatsia Презентация на тему Основные положения молекулярно-кинетической теории
Презентация на тему Основные положения молекулярно-кинетической теории  изические основы микроэлектроники
изические основы микроэлектроники