Содержание
- 2. ФГБОУ ГУМРФ Овсянников Михаил Константинович доктор технических наук, профессор; Орлова Елена Геннадьевна кандидат технических наук, доцент;
- 3. Курс «Техническая термодинамика и теплопередача» предназначен для подготовки инженеров по специальности 180405 «Эксплуатация судовых энергетических установок»
- 4. Оглавление ВВЕДЕНИЕ РАЗДЕЛ I. ТЕХНИЧЕСКАЯ ТЕРМОДИНАМИКА Глава 1. ГАЗ КАК РАБОЧЕЕ ТЕЛО. ОСНОВНЫЕ ПАРАМЕТРЫ СОСТОЯНИЯ. УРАВНЕНИЕ
- 5. Оглавление Глава 8. ТЕЧЕНИЕ УПРУГОЙ СРЕДЫ Глава 9. ТЕРМОДИНАМИЧЕСКИЕ ЦИКЛЫ ХОЛОДИЛЬНЫХ УСТАНОВОК Глава 10. ГАЗОВЫЕ СМЕСИ
- 6. Часть 1 Техническая термодинамика ФГБОУ ГУМРФ
- 7. Первая часть курса «Техническая термодинамика» содержит общие сведения о параметрах, характеристиках и теплофизических свойствах рабочих сред
- 8. Глава 1. ГАЗ КАК РАБОЧЕЕ ТЕЛО. ОСНОВНЫЕ ПАРАМЕТРЫ СОСТОЯНИЯ. УРАВНЕНИЕ СОСТОЯНИЯ ФГБОУ ГУМРФ
- 9. 1.1. Идеальный газ. Параметры состояния Идеальным газом принято называть модель газа, в которой: а) общий объем
- 10. Параметры состояния Состояние любого газа характеризуется тремя основными параметрами: Удельный объем υ, м3/кг; υ = V/m,
- 11. Давление 1 бар = 105 Па; 1 атм ≈ 101325 Па; 1 МПа = 106 Па;
- 12. 1.2. Уравнение состояния (Клайперона – Менделеева) где µ, кг/(кмоль) – молекулярная масса газа. Величина R0 =
- 13. Формы записи уравнения состояния Дж/(кг ·К) - «массовая газовая постоянная» Или: pυ= RT Или : pV
- 14. 1.3. Термодинамический процесс. Графическое изображение процесса Непрерывная совокупность изменяющихся состояний рабочего тела называется термодинамическим процессом. Если
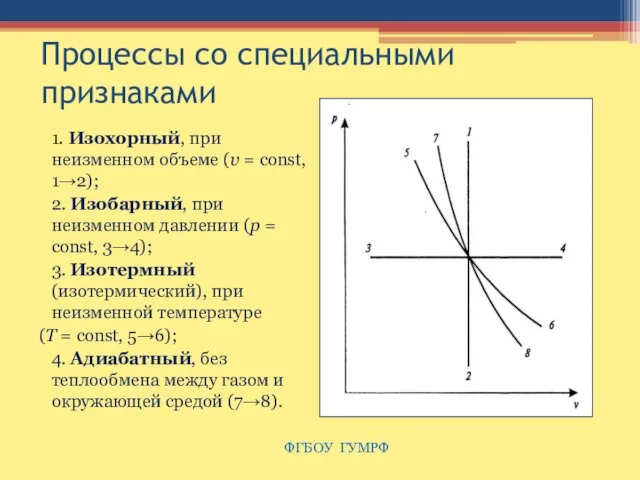
- 15. Процессы со специальными признаками 1. Изохорный, при неизменном объеме (υ = const, 1→2); 2. Изобарный, при
- 16. 1.4. Теплоемкость Количество теплоты, необходимое для изменения температуры 1 кг вещества на 1 К, называется его
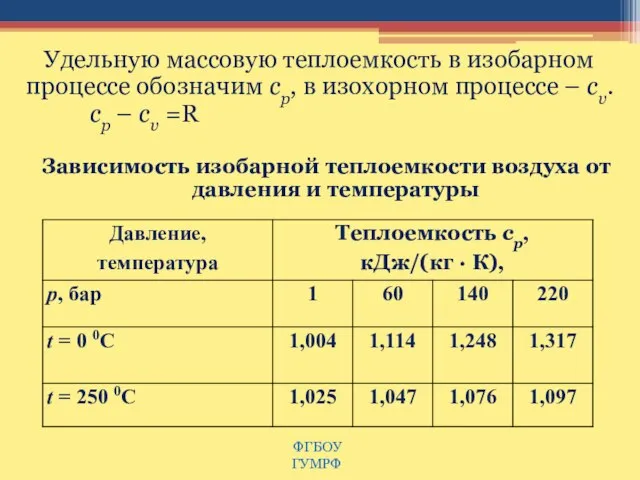
- 17. Удельную массовую теплоемкость в изобарном процессе обозначим ср, в изохорном процессе – сυ. ср – сυ
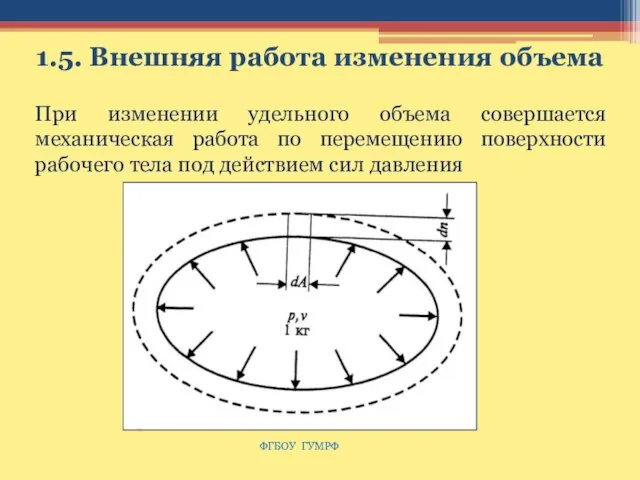
- 18. 1.5. Внешняя работа изменения объема При изменении удельного объема совершается механическая работа по перемещению поверхности рабочего
- 19. ФГБОУ ГУМРФ Удельная работа расширения газа, находящегося под давлением р при элементарном изменении объема (dυ =
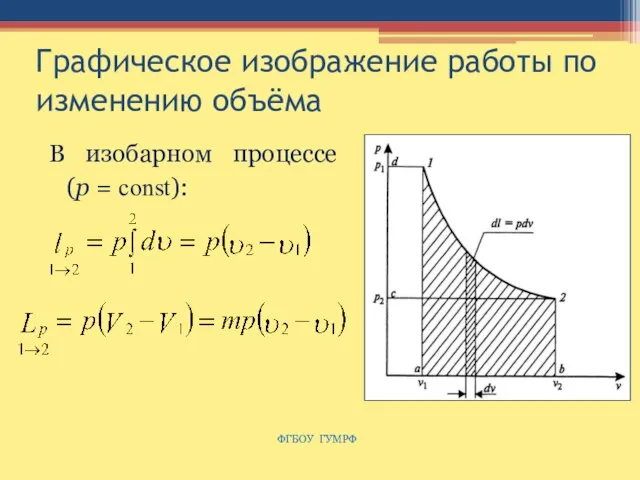
- 20. Графическое изображение работы по изменению объёма В изобарном процессе (р = const): ФГБОУ ГУМРФ
- 21. Контрольные вопросы и задания к главе 1 Какое состояние называется равновесным состоянием газа? Назвать основные термодинамические
- 22. ФГБОУ ГУМРФ 8. Что называется уравнением состояния газа? 9. Написать уравнение состояния идеального газа. 10. Какая
- 23. Глава 2. ФУНКЦИИ СОСТОЯНИЯ. ПЕРВЫЙ ЗАКОН ТЕРМОДИНАМИКИ 2.1. Функции состояния газа Функция состояния — это функция,
- 24. Функции состояния ФГБОУ ГУМРФ Дифференциал некоторой функции Z = Z(x,y): является полным дифференциалом, при условии: Состояние
- 25. 2.1.1. Внутренняя энергия ФГБОУ ГУМРФ Под внутренней энергией газа понимается суммарная энергия движения его частиц. Она
- 26. 2.1.2. Энтальпия Энтальпией называется полная энергия не перемещающегося газа, которая складывается из внутренней энергии и энергии
- 27. 2.1.3. Энтропия Удельной энтропией называется функция состояния s (Дж/(кг·К), для которой : . С учётом 1-го
- 28. Энтропия ФГБОУ ГУМРФ Величина является полным дифференциалом функции s, следовательно s является функцией состояния. Энтропия произвольной
- 29. 2.2. Первый закон термодинамики ФГБОУ ГУМРФ Первым законом термодинамики называется закон сохранения энергии применительно к термодинамической
- 30. Контрольные вопросы и задания к главе 2 Что называется внутренней энергией газа, назвать ее размерность. Что
- 31. Глава 3. ТЕРМОДИНАМИЧЕСКИЕ ПРОЦЕССЫ 3.1. Политропный процесс Термодинамический процесс, единственным отличительным признаком которого является постоянство теплоемкости
- 32. Уравнение политропного процесса - показатель политропного процесса ФГБОУ ГУМРФ
- 33. 3.2. Уравнения характерных термодинамических процессов Изохорный Изобарный Изотермический Адиабатный (где k – показатель адиабаты) cn =
- 34. 3.3. Работа изменения объема газа в политропном процессе ФГБОУ ГУМРФ Удельная работа в политропном процессе:
- 35. 3.3. Работа изменения объема газа в политропном процессе рυ = р1υ1 = р2υ2 = const В
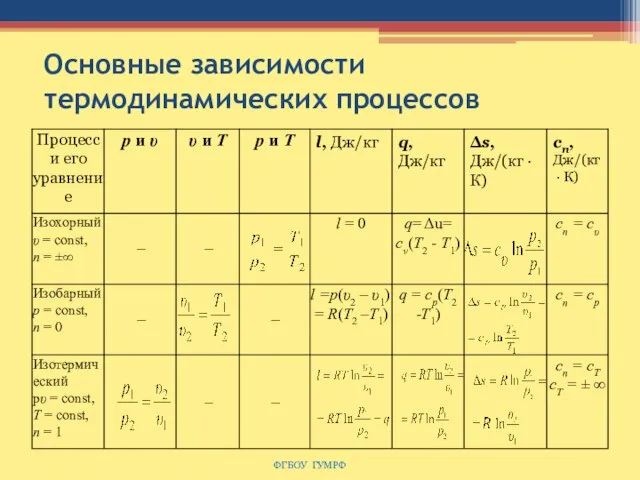
- 36. Основные зависимости термодинамических процессов ФГБОУ ГУМРФ
- 37. Основные зависимости термодинамических процессов ФГБОУ ГУМРФ
- 38. Контрольные вопросы и задания к главе 3 1. Какой процесс называется политропным? 2. Напишите уравнения политропного
- 39. Глава 4. ТЕРМОДИНАМИЧЕСКИЕ ЦИКЛЫ. ВТОРОЙ ЗАКОН ТЕРМОДИНАМИКИ 4.1. Термодинамический цикл. Тепловой двигатель. Понятие термодинамического КПД теплового
- 40. Термодинамический цикл Непрерывная замкнутая совокупность термодинамических процессов образует термодинамический цикл. ФГБОУ ГУМРФ На протяжении цикла 1
- 41. Тепловой двигатель. Устройство для многократного воспроизводства термодинамического цикла, в котором подводимая к рабочему телу теплота преобразуется
- 42. Понятие термодинамического КПД Отношение полезной механической работы цикла (l) к количеству подведенной к рабочему телу теплоты
- 43. 4.2. Второй закон термодинамики Формулировки второго закона термодинамики : природа стремится к переходу от менее вероятных
- 44. 4.3. Второй закон термодинамики для обратимого термодинамического цикла. В результате совершения термодинамического цикла рабочее тело приходит
- 45. ФГБОУ ГУМРФ Выражение (4.1) называется математической формулировкой второго закона термодинамики. Для нулевого результата суммирования выражения (4.1)
- 46. ФГБОУ ГУМРФ Следовательно, с учётом выражения для КПД, можно утверждать, что термодинамический КПД земного теплового двигателя
- 47. 4.4. Второй закон термодинамики для необратимых процессов. Согласно второму закону термодинамики природа стремится к переходу от
- 48. Второй закон термодинамики для необратимых процессов ФГБОУ ГУМРФ Для обратимых циклов интеграл Клаузиса: Общая математическая формула
- 49. Второй закон термодинамики для необратимых процессов dS≥ 0 второй закон термодинамики часто называют законом возрастания энтропии
- 50. 4.5. Цикл Карно Рассмотрим цикл, состоящий из двух изотерм и двух адиабат ФГБОУ ГУМРФ Термический КПД
- 51. Цикл Карно ФГБОУ ГУМРФ В любом другом цикле q1 ≤ q1k q2 ≥q2k Цикл Карно имеет
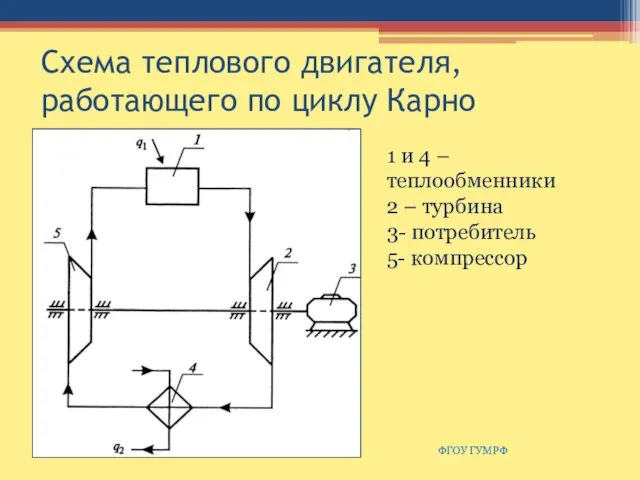
- 52. Схема теплового двигателя, работающего по циклу Карно ФГБОУ ГУМРФ 1 и 4 – теплообменники 2 –
- 53. Контрольные вопросы и задания к главе 4 1. Что называется термодинамическим циклом? 2. Что называется термодинамическим
- 54. Контрольные вопросы и задания к главе 4 7. Почему обратимый цикл Карно считается образцовым? 8. Сформулировать
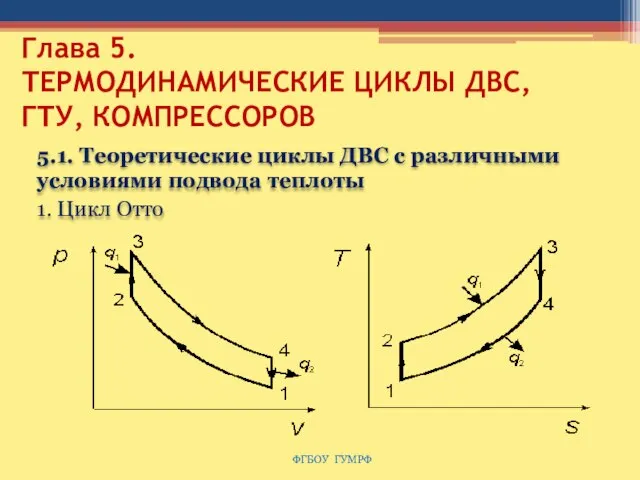
- 55. Глава 5. ТЕРМОДИНАМИЧЕСКИЕ ЦИКЛЫ ДВС, ГТУ, КОМПРЕССОРОВ 5.1. Теоретические циклы ДВС с различными условиями подвода теплоты
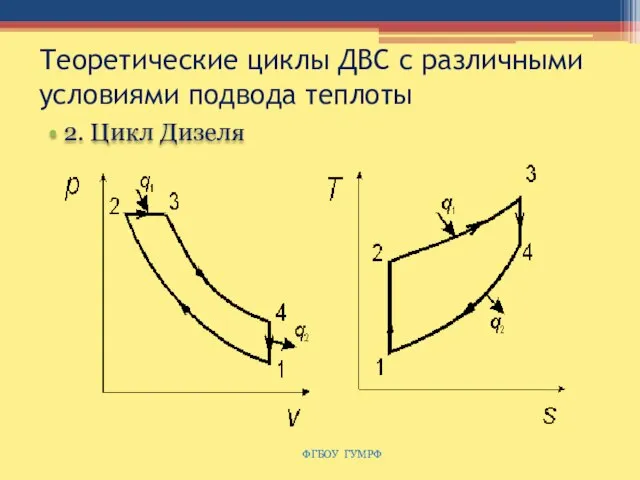
- 56. Теоретические циклы ДВС с различными условиями подвода теплоты 2. Цикл Дизеля ФГБОУ ГУМРФ
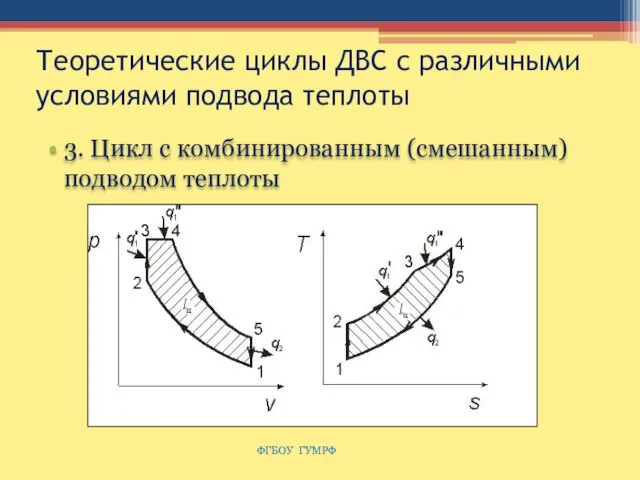
- 57. Теоретические циклы ДВС с различными условиями подвода теплоты 3. Цикл с комбинированным (смешанным) подводом теплоты ФГБОУ
- 58. Характеристики циклов степень сжатия степень повышения давления степень предварительного расширения термический КПД цикла ФГБОУ ГУМРФ
- 59. Термический КПД циклов ДВС Общая формула в цикле Дизеля, λ = 1 в цикле Отто, ρ
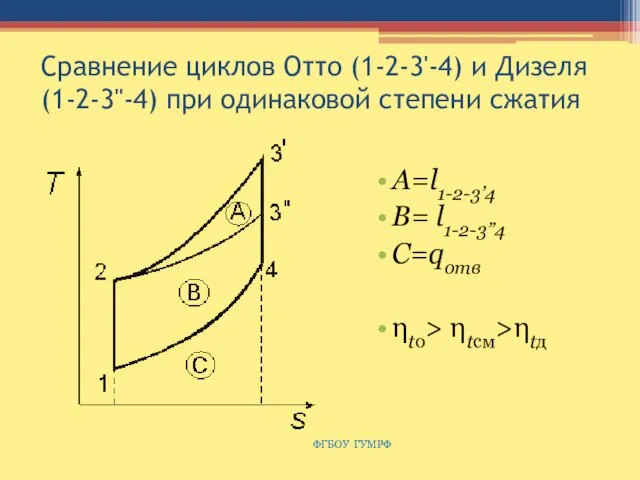
- 60. Сравнение циклов Отто (1-2-3'-4) и Дизеля (1-2-3''-4) при одинаковой степени сжатия А=l1-2-3’4 B= l1-2-3”4 C=qотв ηtо>
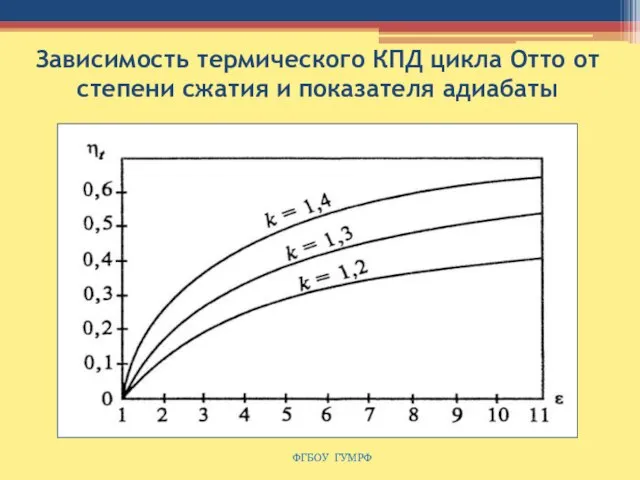
- 61. Зависимость термического КПД цикла Отто от степени сжатия и показателя адиабаты ФГБОУ ГУМРФ
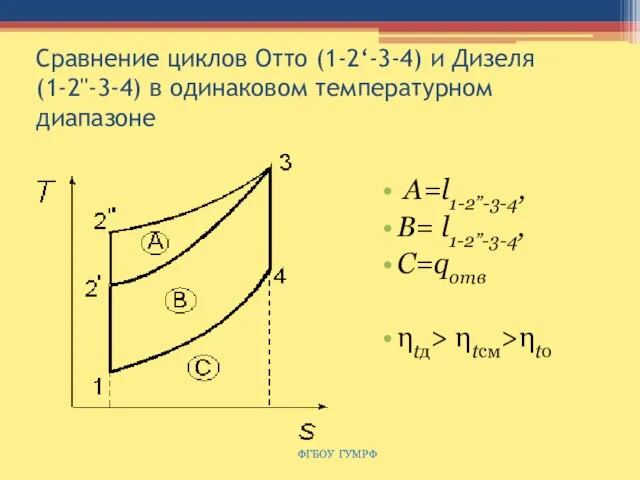
- 62. Сравнение циклов Отто (1-2‘-3-4) и Дизеля (1-2''-3-4) в одинаковом температурном диапазоне А=l1-2”-3-4, B= l1-2”-3-4, C=qотв ηtд>
- 63. 5.2. Коэффициенты полезного действия теплового двигателя Относительный внутренний КПД теплового двигателя: η0i = l i’/li где
- 64. Коэффициенты полезного действия теплового двигателя механический КПД эффективный КПД где ge= Вч/Ре – удельный эффективный расход
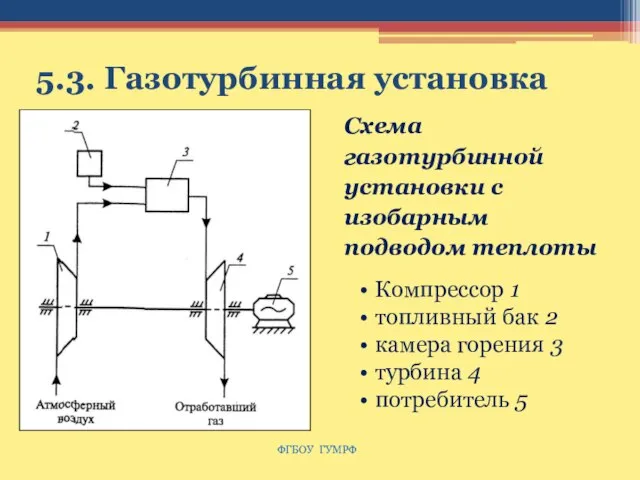
- 65. 5.3. Газотурбинная установка Схема газотурбинной установки с изобарным подводом теплоты Компрессор 1 топливный бак 2 камера
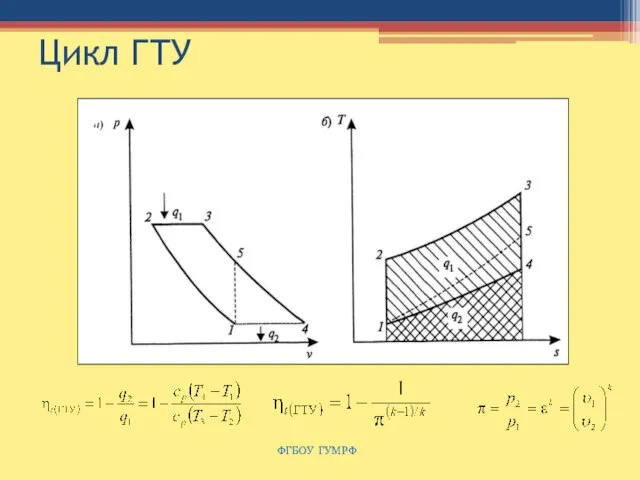
- 66. Цикл ГТУ ФГБОУ ГУМРФ
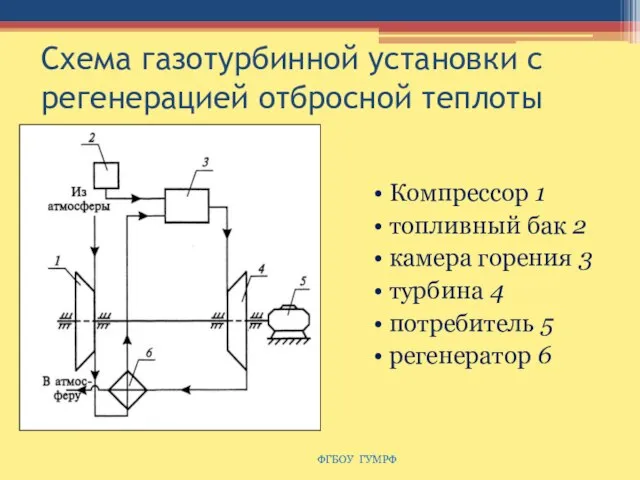
- 67. Схема газотурбинной установки с регенерацией отбросной теплоты Компрессор 1 топливный бак 2 камера горения 3 турбина
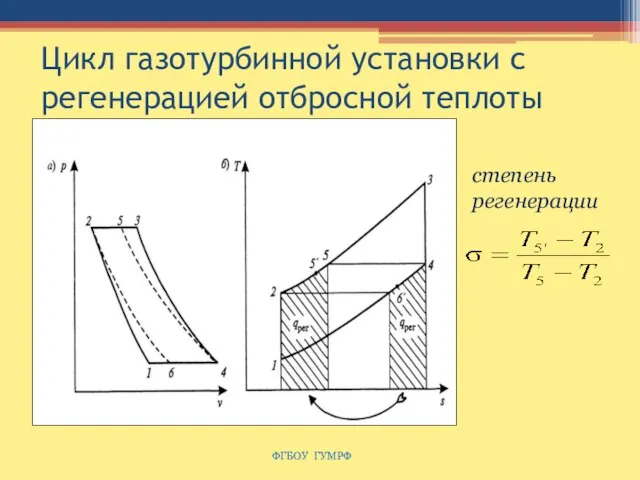
- 68. Цикл газотурбинной установки с регенерацией отбросной теплоты ФГБОУ ГУМРФ степень регенерации
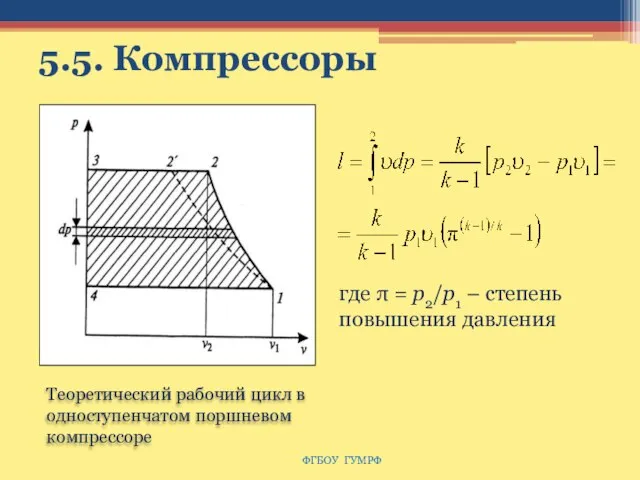
- 69. 5.5. Компрессоры где π = р2/р1 – степень повышения давления ФГБОУ ГУМРФ Теоретический рабочий цикл в
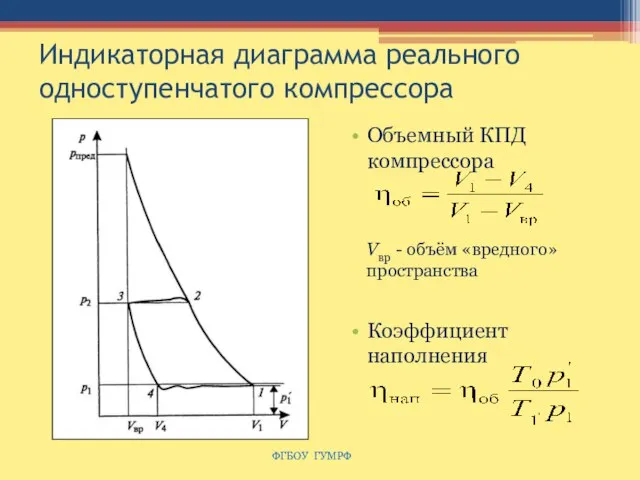
- 70. Индикаторная диаграмма реального одноступенчатого компрессора Объемный КПД компрессора Коэффициент наполнения ФГБОУ ГУМРФ Vвр - объём «вредного»
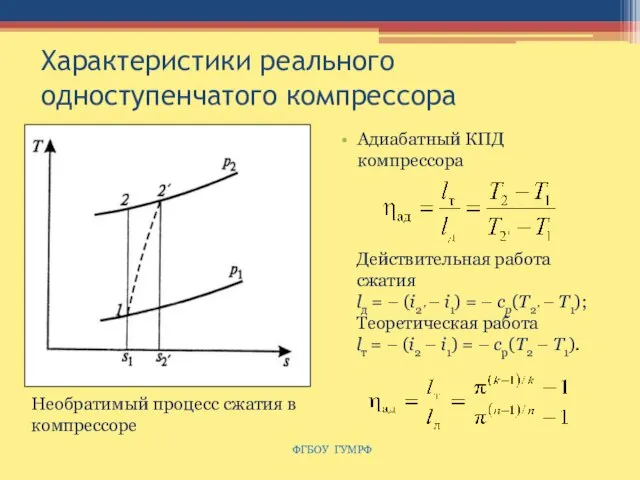
- 71. Характеристики реального одноступенчатого компрессора Адиабатный КПД компрессора ФГБОУ ГУМРФ Необратимый процесс сжатия в компрессоре Действительная работа
- 72. Характеристики реального одноступенчатого компрессора Реальная удельная работа цикла Массовая производительность одного цилиндра компрессора (кг/с) где n
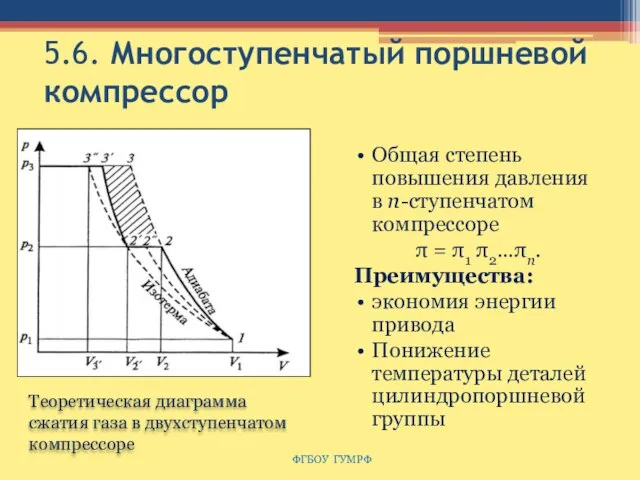
- 73. 5.6. Многоступенчатый поршневой компрессор Общая степень повышения давления в n-ступенчатом компрессоре π = π1 π2…πn. Преимущества:
- 74. Контрольные вопросы и задания к главе 5 Почему современные поршневые двигатели внутреннего сгорания (ДВС) не проектируют
- 75. Контрольные вопросы и задания к главе 5 Определить термический КПД теоретического цикла ГТУ с регенерацией отбросной
- 76. Глава 6. РЕАЛЬНЫЙ ГАЗ. ФАЗОВЫЕ ПРЕВРАЩЕНИЯ 6.1. Уравнение Ван-дер-Ваальса. Пограничные кривые агрегатных состояний ФГБОУ ГУМРФ
- 77. Реальный газ Модель идеального газа не учитывает объем, занимаемый самими молекулами газа, и силы притяжения между
- 78. Реальный газ Все частицы газа гравитационно взаимодействуют между собой. Это взаимодействие оказывается уравновешенным для всех частиц,
- 79. Уравнение Ван-дер-Ваальса Учет внутреннего давления в уравнении состояния достигается прибавлением к абсолютному давлению величины внутреннего давления.
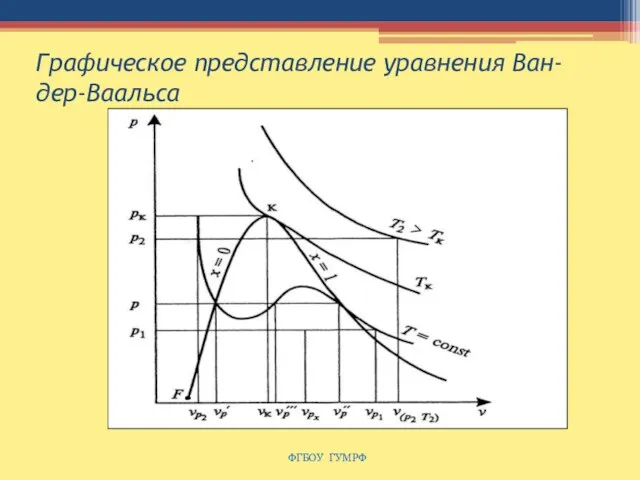
- 80. Графическое представление уравнения Ван-дер-Ваальса ФГБОУ ГУМРФ
- 81. Пограничные кривые агрегатных состояний При υp = υp" газ представляет собой сухой насыщенный пар. Точка υp
- 82. Пограничные кривые агрегатных состояний Переход из газообразного состояния в жидкое через двухфазное состояние (газ — жидкость)
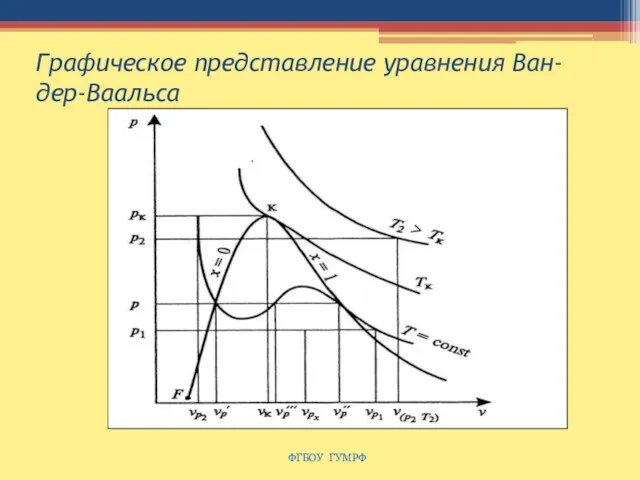
- 83. Графическое представление уравнения Ван-дер-Ваальса ФГБОУ ГУМРФ
- 84. Пограничные кривые агрегатных состояний Вещество в состоянии с параметрами υк, рк, Тк утрачивает четко выраженные свойства
- 85. Пограничные кривые агрегатных состояний Наличие критической точки на изотерме Ван-дер-Ваальса означает, что для каждой жидкости существует
- 86. Пограничные кривые агрегатных состояний Непрерывная последовательность точек на диаграммах р–υ, T–s и т. п., соответствующих состояниям
- 87. Пограничные кривые агрегатных состояний Критическая точка «к» делит ее на нижнюю (левую) пограничную кривую, точки которой
- 88. Пограничные кривые агрегатных состояний При параметрах слева от нижней пограничной кривой рабочее тело находится в жидком
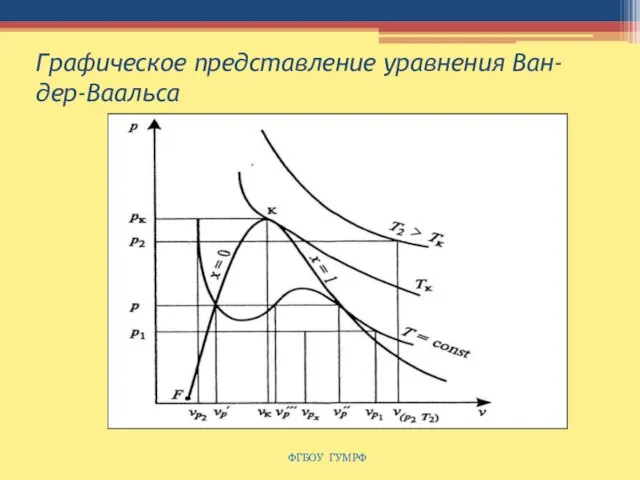
- 89. Графическое представление уравнения Ван-дер-Ваальса ФГБОУ ГУМРФ
- 90. Пограничные кривые агрегатных состояний Переход в изобарном процессе с левой ветви пограничной кривой на правую ветвь
- 91. Пограничные кривые агрегатных состояний Нижняя пограничная кривая начинается в так называемой фундаментальной или тройной критической точке
- 92. 6.2. Пар и его свойства Состоянием насыщения называется такое состояние с параметрами Ts, ps , при
- 93. Пар и его свойства Сухой пар — это пар, не содержащий капелек жидкости. Влажный пар —
- 94. Параметры влажного пара Удельный объём: υрx = xυp" + (1 – x)υp'. Энтальпия: ix = i'(1
- 95. 6.3. Термодинамические свойства воды и водяного пара В фундаментальной (тройной критической) точке вода имеет параметры: pF
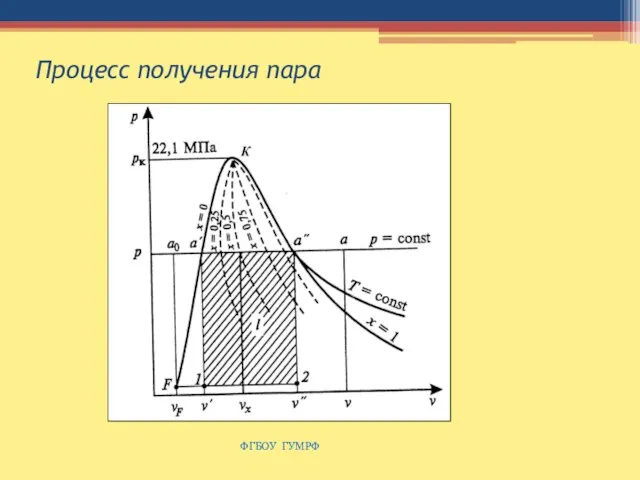
- 96. Процесс получения пара ФГБОУ ГУМРФ
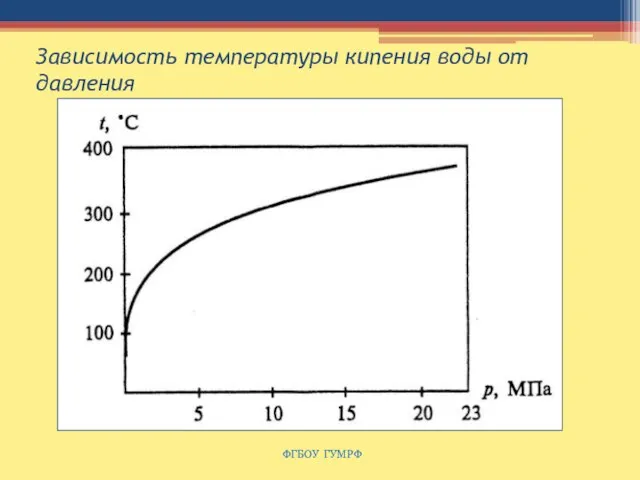
- 97. Зависимость температуры кипения воды от давления ФГБОУ ГУМРФ
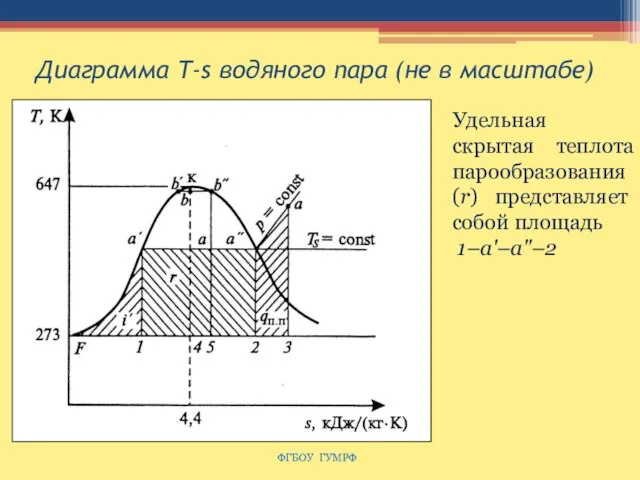
- 98. Диаграмма Т-s водяного пара (не в масштабе) ФГБОУ ГУМРФ Удельная скрытая теплота парообразования (r) представляет собой
- 99. Термодинамические свойства воды и водяного пара Энтальпия сухого насыщенного пара,: i" = i' + r Энтальпия
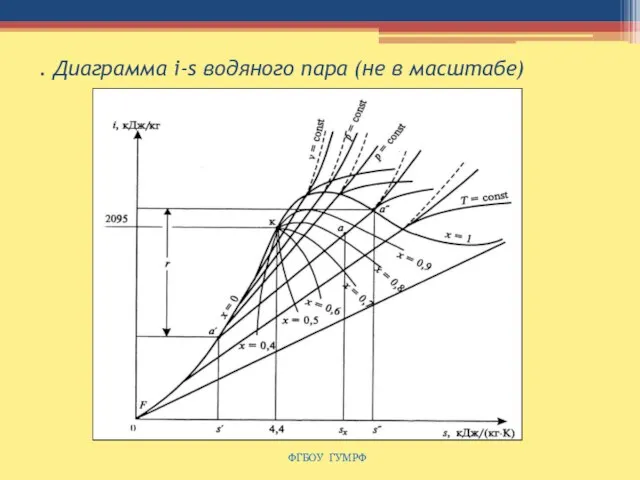
- 100. . Диаграмма i-s водяного пара (не в масштабе) ФГБОУ ГУМРФ
- 101. Контрольные вопросы и задания к главе 6 Назвать основные отличия реального газа от идеального. Написать уравнение
- 102. Глава 7. ЦИКЛЫ ПАРОТУРБИННЫХ УСТАНОВОК 7.1. ЦИКЛЫ ПАРОТУРБИННЫХ УСТАНОВОК. Цикл Ренкина ФГБОУ ГУМРФ
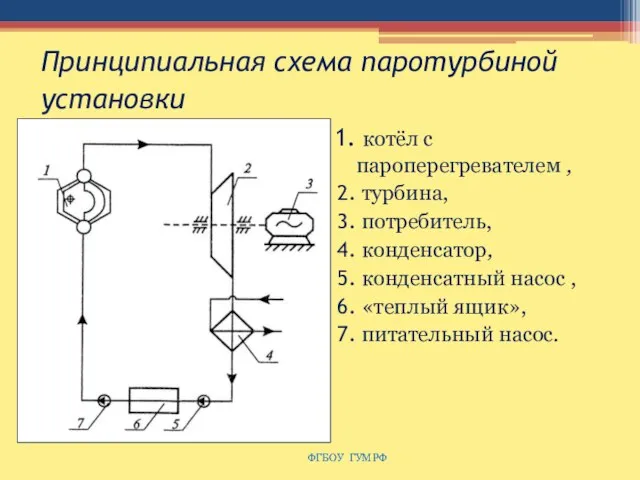
- 103. Принципиальная схема паротурбиной установки котёл с пароперегревателем , турбина, потребитель, конденсатор, конденсатный насос , «теплый ящик»,
- 104. Циклы Ренкина в координатах Т–s 1–2 адиабатическое расширение пара в турбине 2–3 процесс конденсации пара 3-4
- 105. 7.2. Влияние параметров пара на КПД цикла Ренкина h = i1 – i2 полезная работа, q
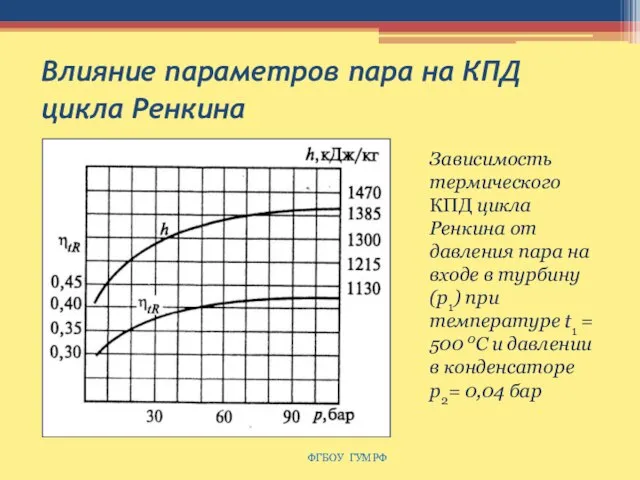
- 106. Влияние параметров пара на КПД цикла Ренкина ФГБОУ ГУМРФ Зависимость термического КПД цикла Ренкина от давления
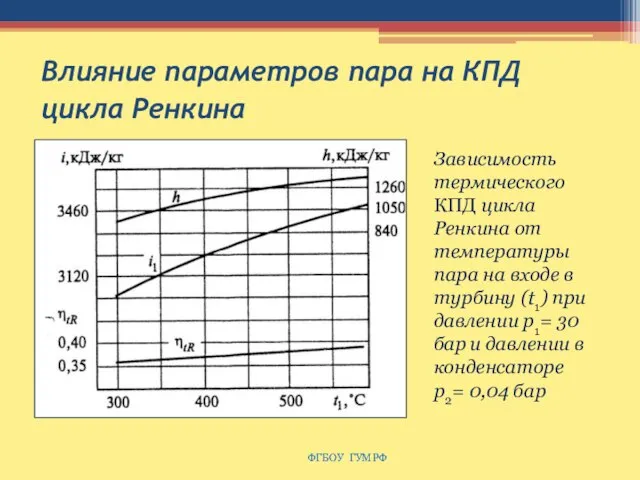
- 107. Влияние параметров пара на КПД цикла Ренкина ФГБОУ ГУМРФ Зависимость термического КПД цикла Ренкина от температуры
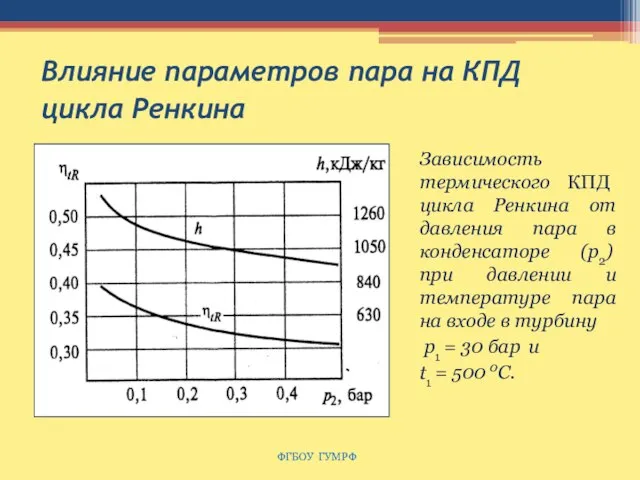
- 108. Влияние параметров пара на КПД цикла Ренкина ФГБОУ ГУМРФ Зависимость термического КПД цикла Ренкина от давления
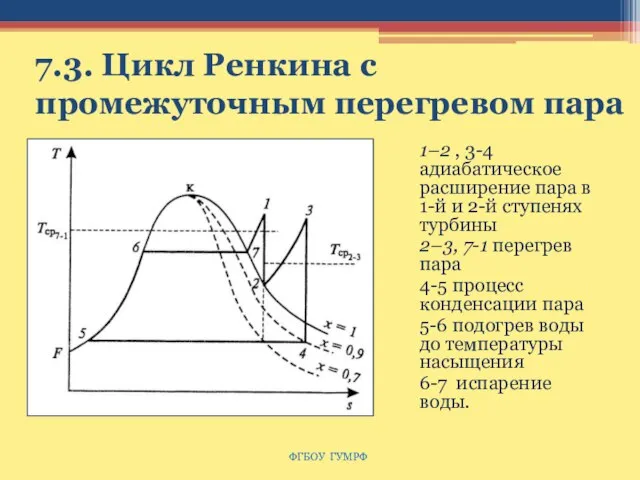
- 109. 7.3. Цикл Ренкина с промежуточным перегревом пара 1–2 , 3-4 адиабатическое расширение пара в 1-й и
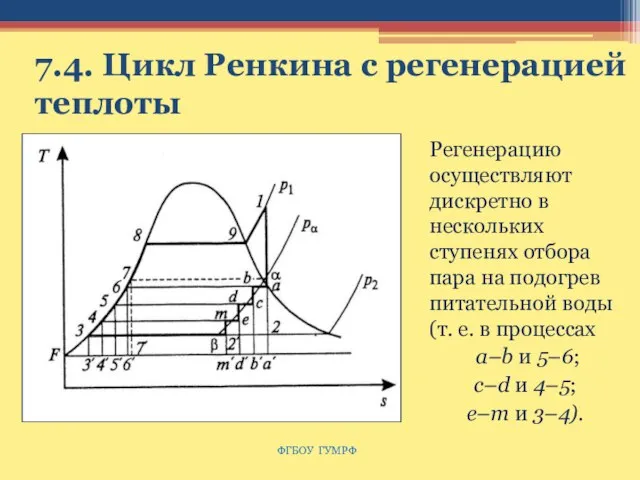
- 110. 7.4. Цикл Ренкина с регенерацией теплоты Регенерацию осуществляют дискретно в нескольких ступенях отбора пара на подогрев
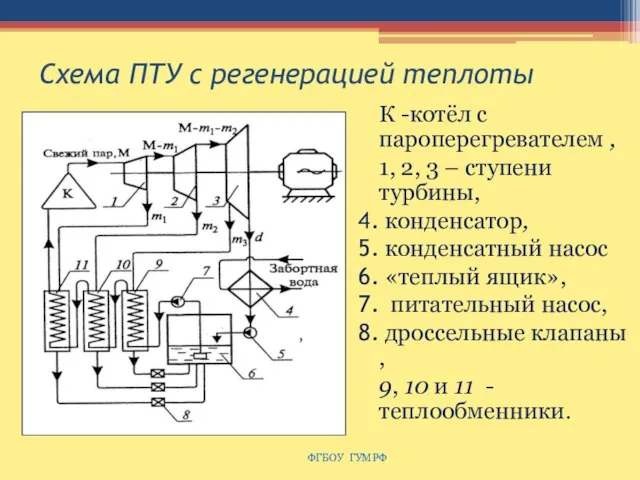
- 111. Схема ПТУ с регенерацией теплоты К -котёл с пароперегревателем , 1, 2, 3 – ступени турбины,
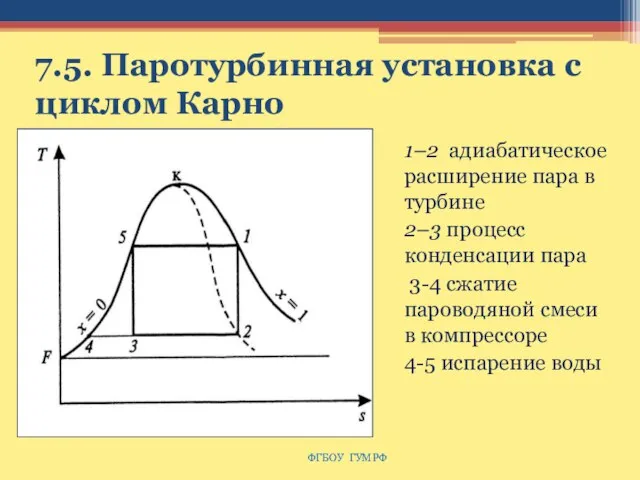
- 112. 7.5. Паротурбинная установка с циклом Карно 1–2 адиабатическое расширение пара в турбине 2–3 процесс конденсации пара
- 113. Контрольные вопросы и задания к главе 7 1. Описать теоретический цикл паротурбинной установки (ПТУ, цикл Ренкина)
- 114. Глава 8. ТЕЧЕНИЕ УПРУГОЙ СРЕДЫ 8.1. Первый закон термодинамики для потока упругой (сжимаемой) среды ФГБОУ ГУМРФ
- 115. Первый закон термодинамики для потока упругой (сжимаемой) среды Работа внешних сил, приложенных к движущейся упругой среде,
- 116. Первый закон термодинамики для потока упругой (сжимаемой) среды В расчете на 1 кг газа: dq +
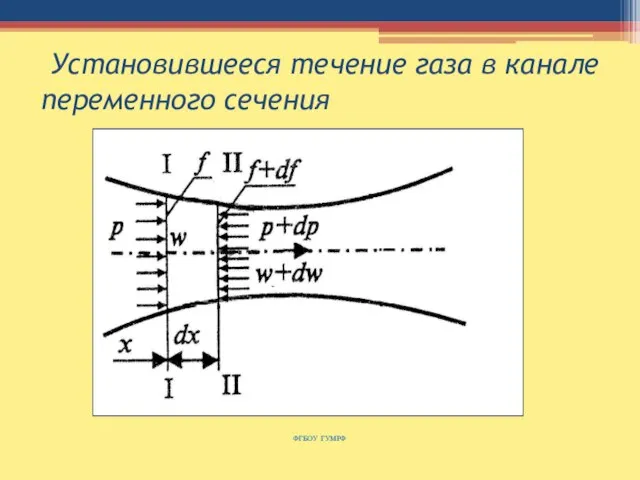
- 117. Первый закон термодинамики для потока упругой (сжимаемой) среды Рассмотрим сплошное, стационарное течение упругой среды в прямом
- 118. Установившееся течение газа в канале переменного сечения ФГБОУ ГУМРФ
- 119. Первый закон термодинамики для потока упругой (сжимаемой) среды В расчете на 1 кг газа: dq +
- 120. Первый закон термодинамики для потока упругой (сжимаемой) среды В расчете на 1 кг газа: dq +
- 121. Первый закон термодинамики для потока упругой (сжимаемой) среды dq = du + d(pυ) + d(w2/2) =
- 122. 8.2. Скорость распространения звука в упругой среде. Числа M и λ Скоростью звука называется скорость распространения
- 123. Скорость распространения звука в упругой среде. Числа M и λ Отношение скорости w движения газа в
- 124. Скорость распространения звука в упругой среде. Числа M и λ Отношение скорости потока в данной точке
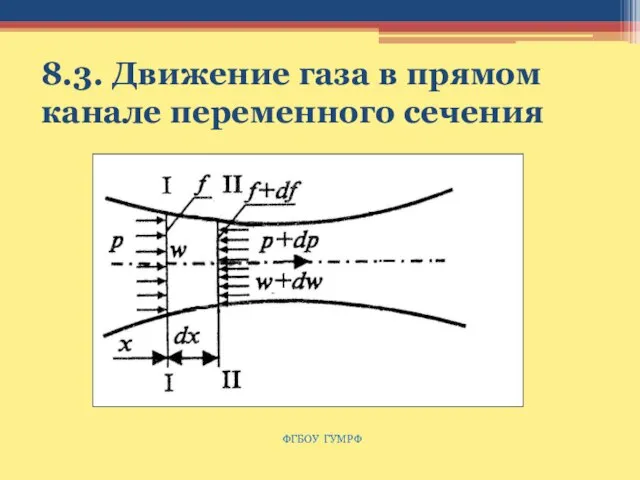
- 125. 8.3. Движение газа в прямом канале переменного сечения ФГБОУ ГУМРФ
- 126. Движение газа в прямом канале переменного сечения Скорость движения в каждом сечении определяется из уравнения сплошности:
- 127. Движение газа в прямом канале переменного сечения Полагаем, что в процессе течения в канале параметры газа
- 128. Движение газа в прямом канале переменного сечения Подставляя выражения (8.6) и (8.7) в (8.5) , получим:
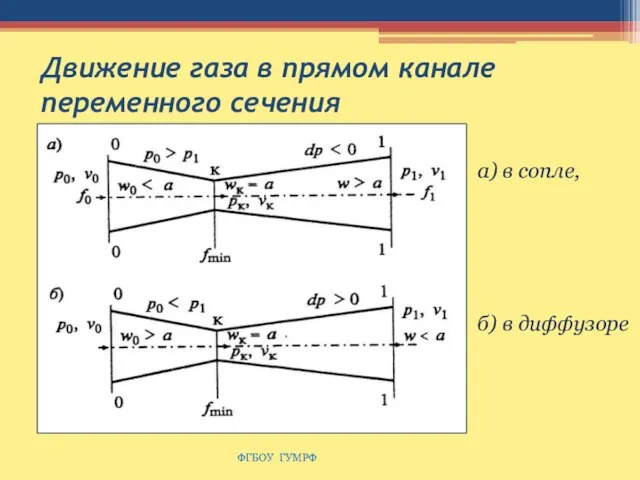
- 129. Движение газа в прямом канале переменного сечения ФГБОУ ГУМРФ а) в сопле, б) в диффузоре
- 130. Движение газа в прямом канале переменного сечения ФГБОУ ГУМРФ Для дальнейшего увеличения скорости течения в канале
- 131. Движение газа в прямом канале переменного сечения ФГБОУ ГУМРФ Канал, по которому газ движется в направлении
- 132. Движение газа в прямом канале переменного сечения ФГБОУ ГУМРФ Канал, по которому газ движется в направлении
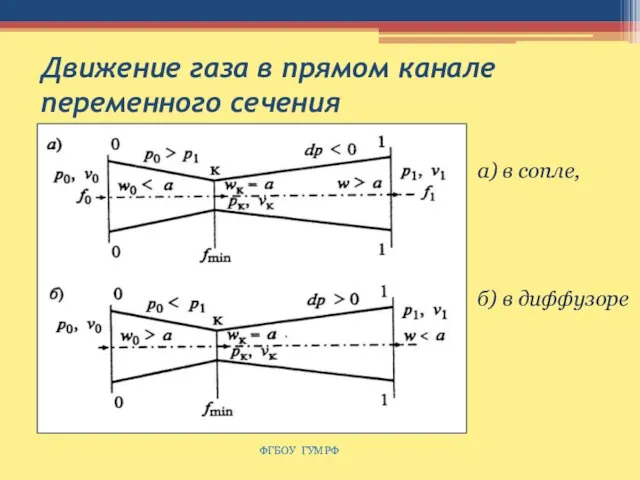
- 133. Движение газа в прямом канале переменного сечения ФГБОУ ГУМРФ а) в сопле, б) в диффузоре
- 134. 8.4. Зависимость скорости истечения газа от перепада давления ФГБОУ ГУМРФ 1-й закон термодинамики: dq = du
- 135. Зависимость скорости истечения газа от перепада давления ФГБОУ ГУМРФ Проинтегрируем уравнение Бернулли υdp + d(w2/2) =
- 136. Зависимость скорости истечения газа от перепада давления ФГБОУ ГУМРФ Когда газ истекает в вакуум (β =
- 137. Зависимость скорости истечения газа от перепада давления ФГБОУ ГУМРФ Откуда критическое отношение давлений : Критическая скорость
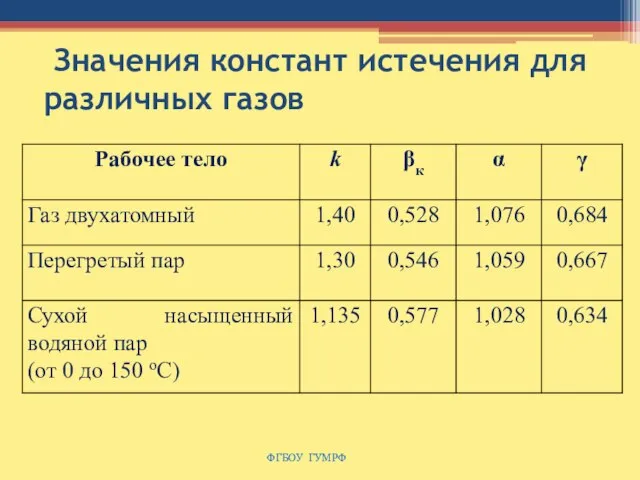
- 138. Значения констант истечения для различных газов ФГБОУ ГУМРФ
- 139. 8.5. Расход газа при истечении из резервуара ФГБОУ ГУМРФ Расход G, (кг/с) определится из уравнения сплошности:
- 140. Расход газа при истечении из резервуара ФГБОУ ГУМРФ При достижении β=βк и критической скорости истечения расход
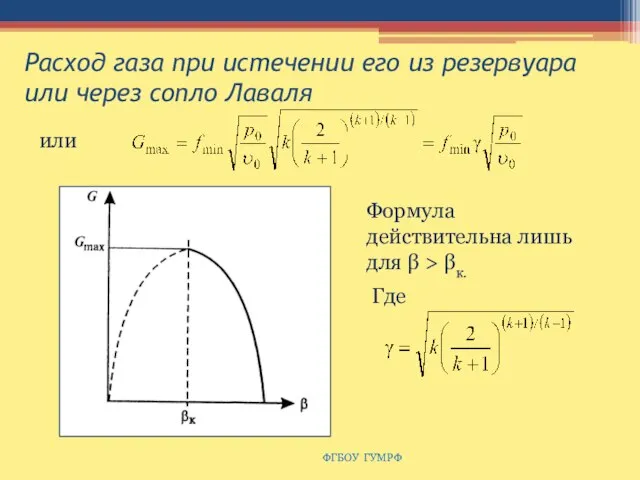
- 141. Расход газа при истечении его из резервуара или через сопло Лаваля ФГБОУ ГУМРФ или Где Формула
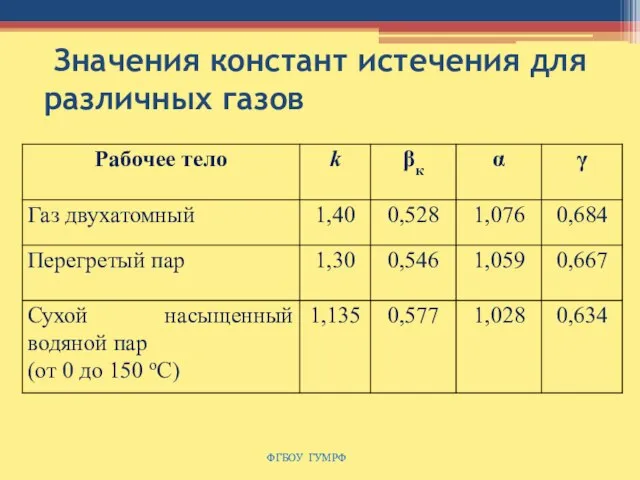
- 142. Значения констант истечения для различных газов ФГБОУ ГУМРФ
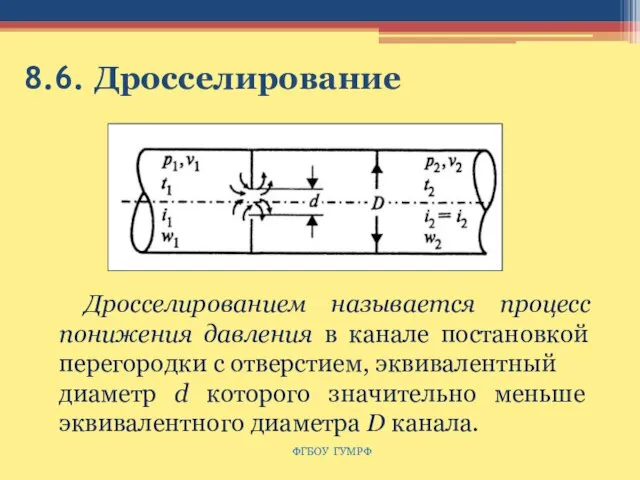
- 143. 8.6. Дросселирование ФГБОУ ГУМРФ Дросселированием называется процесс понижения давления в канале постановкой перегородки с отверстием, эквивалентный
- 144. Дросселирование ФГБОУ ГУМРФ w1 = w2, Т1≈Т2 , р1υ1 = р2υ2 i = const
- 145. Контрольные вопросы и задания к главе 8 1. Сформулировать и написать уравнение первого закона термодинамики для
- 146. Контрольные вопросы и задания к главе 8 6. Что называется критическим отношением давлений при истечении газа
- 147. Глава 9. ТЕРМОДИНАМИЧЕСКИЕ ЦИКЛЫ ХОЛОДИЛЬНЫХ УСТАНОВОК 9.1. Обратный цикл Карно ФГБОУ ГУМРФ Цикл холодильной установки является
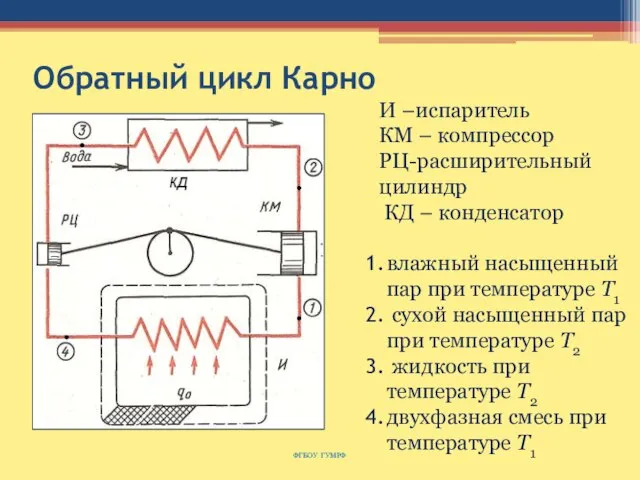
- 148. Обратный цикл Карно ФГБОУ ГУМРФ И –испаритель КМ – компрессор РЦ-расширительный цилиндр КД – конденсатор влажный
- 149. Обратный цикл Карно ФГБОУ ГУМРФ 1-2 – адиабата сжатия 2-3 - конденсация 3-4 – адиабата расширения
- 150. Обратный цикл Карно ФГБОУ ГУМРФ Количество теплоты q0, отводимое от охлаждаемого объекта единицей массы хладагента, называется
- 151. Обратный цикл Карно ФГБОУ ГУМРФ
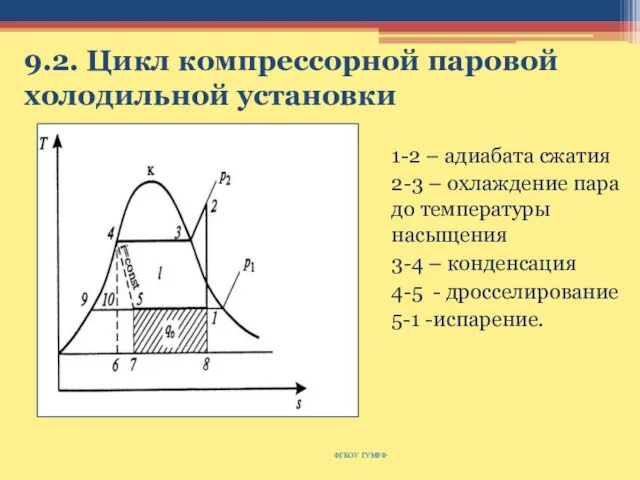
- 152. 9.2. Цикл компрессорной паровой холодильной установки ФГБОУ ГУМРФ 1-2 – адиабата сжатия 2-3 – охлаждение пара
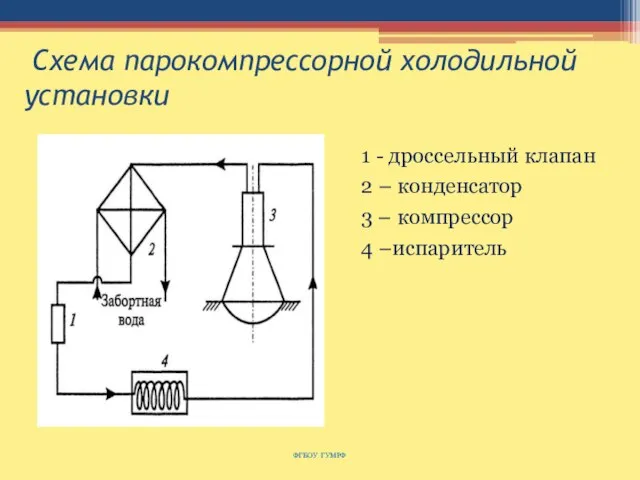
- 153. Схема парокомпрессорной холодильной установки ФГБОУ ГУМРФ 1 - дроссельный клапан 2 – конденсатор 3 – компрессор
- 154. Цикл компрессорной паровой холодильной установки ФГБОУ ГУМРФ Удельная холодопроизводительность: q0 = i1 – i5 Удельное количество
- 155. Контрольные вопросы и задания к главе 9 1. Что представляет собой обратный цикл Карно и в
- 156. Глава 10. ГАЗОВЫЕ СМЕСИ 10.1. Термодинамические характеристики газовых смесей ФГБОУ ГУМРФ Газовой смесью называется смесь газов,
- 157. Термодинамические характеристики газовых смесей ФГБОУ ГУМРФ Каждый из входящих в смесь объемом Vс газов занимает весь
- 158. Термодинамические характеристики газовых смесей ФГБОУ ГУМРФ Масса смеси: Газовая постоянная смеси: где mi = Mi/Mc —
- 159. Термодинамические характеристики газовых смесей ФГБОУ ГУМРФ Объемы одного моля Vμ всех газов при одинаковых давлении и
- 160. 10.2. Атмосферный воздух как газовая смесь ФГБОУ ГУМРФ Влажный воздух рассматривают как газовую смесь сухого воздуха
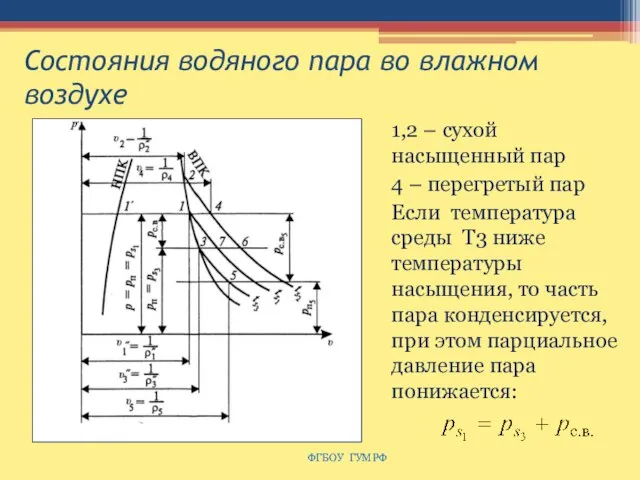
- 161. Состояния водяного пара во влажном воздухе ФГБОУ ГУМРФ 1,2 – сухой насыщенный пар 4 – перегретый
- 162. Состояния водяного пара во влажном воздухе ФГБОУ ГУМРФ Абсолютная влажность зависит не от общего давления в
- 163. Состояния водяного пара во влажном воздухе ФГБОУ ГУМРФ Если общее давление среды р больше парциального давления
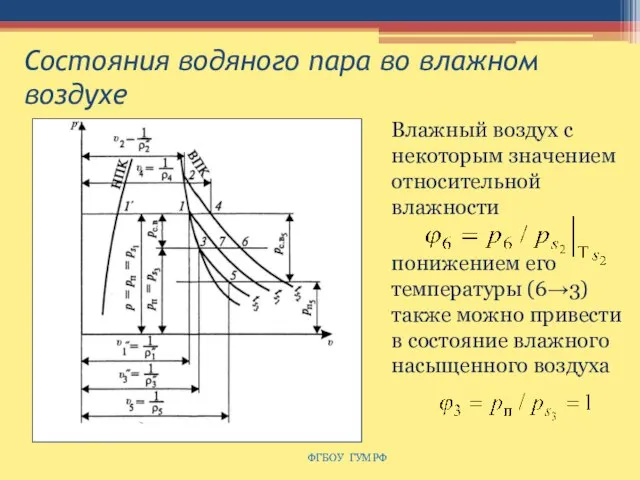
- 164. Состояния водяного пара во влажном воздухе ФГБОУ ГУМРФ Влажный воздух с некоторым значением относительной влажности понижением
- 165. Состояния водяного пара во влажном воздухе ФГБОУ ГУМРФ Состояние, при котором парциальное давление пара равно давлению
- 166. Состояния водяного пара во влажном воздухе ФГБОУ ГУМРФ Разделим почленно одно на другое два уравнения состояния
- 167. 10.3. Способы определения относительной влажности. Диаграмма i–d ФГБОУ ГУМРФ Металлический тонкостенный цилиндр, заполненный эфиром, прокачивается воздухом.
- 168. Гигрометр ФГБОУ ГУМРФ На р–υ-диаграмме отмечаются точки (7 — по термометру в воздухе и 3 —
- 169. Психрометр ФГБОУ ГУМРФ Психрометр состоит из двух термометров: сухого и смоченного. Головка с ртутью смоченного термометра
- 170. Характеристики влажного воздуха ФГБОУ ГУМРФ Газовая постоянная влажного воздуха где rс.в.и rп — объемные доли сухого
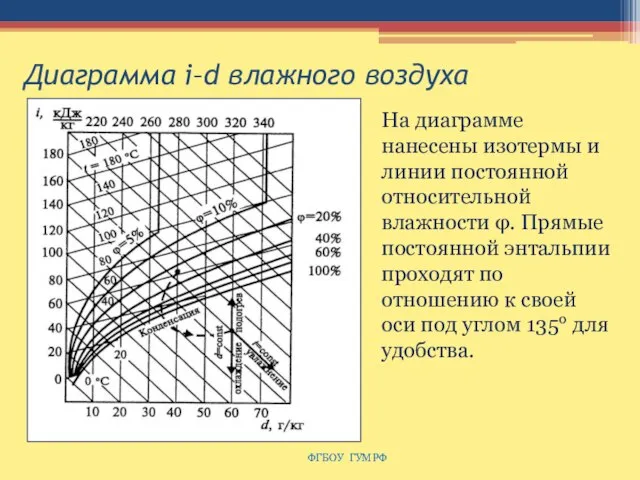
- 171. Диаграмма i–d влажного воздуха ФГБОУ ГУМРФ На диаграмме нанесены изотермы и линии постоянной относительной влажности φ.
- 173. Скачать презентацию

























































































































 Инфракрасное излучение в помощь школе
Инфракрасное излучение в помощь школе Презентация на тему Энергосберегающие лампы
Презентация на тему Энергосберегающие лампы  Матрица
Матрица Ремонт клиновой и параллельной (двухдисковой) задвижки
Ремонт клиновой и параллельной (двухдисковой) задвижки Элементы теории поля, используемые в электрофизиологии
Элементы теории поля, используемые в электрофизиологии Тепловое действие тока. Закон Джоуля-Ленца
Тепловое действие тока. Закон Джоуля-Ленца Давление газа
Давление газа Реактивное движение. Ракеты
Реактивное движение. Ракеты Примеры решения задач по теме Кинематика твёрдого тела
Примеры решения задач по теме Кинематика твёрдого тела Презентация на тему Переменный электрический ток
Презентация на тему Переменный электрический ток  Тема 3-6 Измерители направления ветра с сельсинной передачей
Тема 3-6 Измерители направления ветра с сельсинной передачей Электрический двигатель постоянного тока. Лабораторная работа
Электрический двигатель постоянного тока. Лабораторная работа Домашнее задание по физике
Домашнее задание по физике Математический аппарат термодинамики. Термодинамические потенциалы. Характеристические функции
Математический аппарат термодинамики. Термодинамические потенциалы. Характеристические функции Источники света. Прямолинейное распространение света,
Источники света. Прямолинейное распространение света, Модель двигателя внешнего сгорания Стирлинга
Модель двигателя внешнего сгорания Стирлинга Презентация на тему Деление ядер урана Атомная энергетика
Презентация на тему Деление ядер урана Атомная энергетика  Презентация на тему Цепные ядерные реакции
Презентация на тему Цепные ядерные реакции  Масса тела
Масса тела Лекция №14. Интегралы, зависящие от параметров
Лекция №14. Интегралы, зависящие от параметров Напряжение в точке включения реактора. Распределение напряжения по линии. Задача
Напряжение в точке включения реактора. Распределение напряжения по линии. Задача Ложные воспоминания
Ложные воспоминания Фотометрия Бугера, Ламберта, Бера
Фотометрия Бугера, Ламберта, Бера Основы термодинамики. Внутренняя энергия
Основы термодинамики. Внутренняя энергия Каковы основные положения молекулярной теории строения вещества?
Каковы основные положения молекулярной теории строения вещества? Постоянный электрический ток
Постоянный электрический ток Устойчивость режима работы реактора. Лекция № 5
Устойчивость режима работы реактора. Лекция № 5 Механические колебания и волны. Звук
Механические колебания и волны. Звук