Содержание
- 2. Атом водорода прост, поскольку он включает лишь один электрон: его потенциальная энергия обусловлена только электростатическим притяжением.
- 3. Как ни странно, уровни энергии многоэлектронных атомов оказываются непосредственно связанными с уровнями*атома водорода. Эта связь настолько
- 4. Однако расстояния между уровнями энергии у многоэлектронных атомов не связаны такой простой зависимостью, как уровни атома
- 5. Теперь попробуем учесть межэлектронное отталкивание. Как при этом изменится движение электронов и их уровни энергии? Во-первых,
- 6. Тогда расстояние между ними вдвое превышало бы радиус орбитали (0,39 А). Энергия отталкивания двух электронов, отстоящих
- 8. Рассмотрим 2s- и 2p-уровни. Эти ячейки расположены при значениях энергии, соответствующих таким состояниям, когда один из
- 9. Необходимо отметить и вторую особенность 2s- и 2p – орбиталей атома гелия. Энергии 2s- и 2p-орбиталей
- 10. б) Атом лития Возвращаясь к нашей простой модели с «выключенным» отталкиванием электронов, можно было бы попробовать
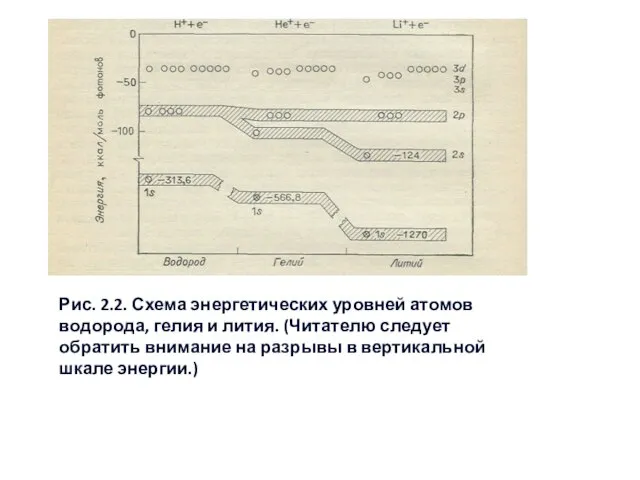
- 11. Рис. 2.2. Схема энергетических уровней атомов водорода, гелия и лития. (Читателю следует обратить внимание на разрывы
- 12. Согласно принципу Паули, если два электрона уже заняли одну 1s-орбиталь, третий электрон не сможет находиться там
- 13. Так же как у атома гелия, 2s- и 2р-состояния не идентичны по энергии. Межэлектронное отталкивание расщепляет
- 14. Зная величину эффективного заряда ядра, с помощью уравнения (1-12) можно найти средний радиус орбитали Мы обнаруживаем
- 15. Для лития в состоянии Li (1s22р) можно провести совершенно аналогичное рассуждение. 2p -Электрон удаляется легче —
- 16. Ясно, что для 2р – электрона это гораздо сложнее. Вследствие узловых свойств 2р – электрона вероятность
- 17. в) Вперед к неону Теперь, зная общие принципы, можно попытаться проследить за тенденциями вдоль всего периода
- 18. Однако, когда мы переходим к бору, пятый электрон разместить ни на 1s-, ни на 2s-орбитали нельзя.
- 19. Положение становится более благоприятным, когда один электрон располагается на 2рx – орбитали, а второй уходит либо
- 20. Для рассмотрения фтора и неона не требуется вводить никаких, новых представлений. Их дополнительные электроны приходят на
- 21. Как показано на рис. 2.4, переход от неона к натрию сопровождается таким же резким уменьшением энергии
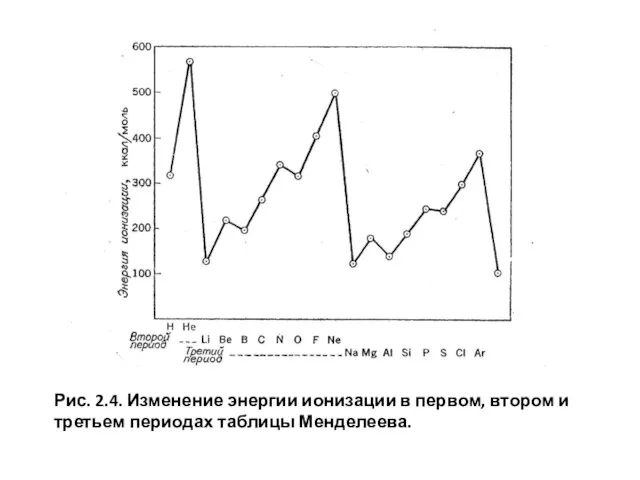
- 22. Рис. 2.4. Изменение энергии ионизации в первом, втором и третьем периодах таблицы Менделеева.
- 23. г) Эффективный заряд ядра во втором периоде С помощью нашего одноэлектронного приближения*) можно теперь исследовать эффективный
- 24. (2 – 5) Определив значение Z*, можно вычислить средний радиус одноэлектронных орбиталей с помощью модифицированного уравнения
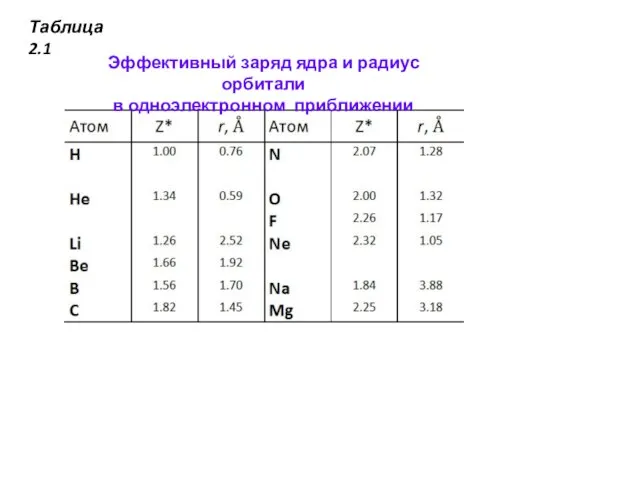
- 25. Таблица 2.1 Эффективный заряд ядра и радиус орбитали в одноэлектронном приближении
- 26. д) Спин электрона и принцип Паули Тщательные измерения показывают, что электрон обладает не только электростатическими, но
- 27. Как возникает магнитное поле электрона? В макромире магнитное поле возникает при движении электрического заряда по круговой
- 28. Подробно рассматривать эту проблему нам не обязательно. Достаточно сказать, что спин электрона (или магнитное поле) может
- 29. Величина ½ представляет собой коэффициент расхождения между экспериментом и простым расчетом для отношения момента к полю.
- 30. то сюда же может прийти и второй — тогда мы проведем черточку справа налево; получившийся при
- 31. 2.2. ЭНЕРГИЯ ИОНИЗАЦИИ И ВАЛЕНТНЫЕ ЭЛЕКТРОНЫ Существует явная зависимость между легкостью отрыва электрона от атома и
- 33. Скачать презентацию
Слайд 2Атом водорода прост, поскольку он включает лишь один электрон: его потенциальная энергия
Атом водорода прост, поскольку он включает лишь один электрон: его потенциальная энергия

Уже при переходе к следующему элементу, атому гелия, эта простота исчезает. Атом гелия имеет два электрона, поэтому его потенциальная энергия состоит из трех слагаемых: каждый электрон притягивается к ядру и; оба электрона отталкиваются друг от друга. Математические трудности мгновенно возрастают до такой степени, что становится необходимым использовать трудоемкие приближенные методы. Положение еще больше усложняется для других элементов периодической системы. Стоит подумать хотя бы об атоме кислорода, который имеет восемь электронов и соответственно восемь членов, отвечающих притяжению электронов к ядру, и двадцать восемь членов, соответствующих отталкиванию между электронами. Неудивительно, что справиться с такими вычислениями может только самый мощный современный компьютер.
Слайд 3Как ни странно, уровни энергии многоэлектронных атомов оказываются непосредственно связанными с уровнями*атома
Как ни странно, уровни энергии многоэлектронных атомов оказываются непосредственно связанными с уровнями*атома

Схема уровней энергии атома водорода нам уже известна, поэтому можно понять и отклонения, обусловленные межэлектронным отталкиванием.
2.1. УРОВНИ ЭНЕРГИИ МНОГОЭЛЕКТРОННЫХ АТОМОВ
В электрическом разряде атомы испускают свет, и цвет, который мы видим при этом, позволяет определить схему уровней энергии атома. Многоэлектронные атомы, как и атом водорода, испускают линейчатый спектр — можно наблюдать только определенные энергии. Таким образом, для объяснения необходима квантовомеханическая модель.
Слайд 4Однако расстояния между уровнями энергии у многоэлектронных атомов не связаны такой простой
Однако расстояния между уровнями энергии у многоэлектронных атомов не связаны такой простой

а) Атом гелия
В качестве простейшего подхода к двухэлектронному атому гелия можно предположить, что каким-то образом нам удалось исключить взаимное отталкивание электронов. Тогда каждый электрон двигался бы вокруг ядра и не замечал бы присутствия другого электрона. Каждый электрон находился бы на 1s-орбитали иона Не+ — на самом низком уровне энергий иона Не+.
Слайд 5Теперь попробуем учесть межэлектронное отталкивание. Как при этом изменится движение электронов и
Теперь попробуем учесть межэлектронное отталкивание. Как при этом изменится движение электронов и

Во-первых, в результате отталкивания электроны будут «стремиться» держаться подальше друг от друга. Если один электрон находится к северу от ядра, то второй постарается оказаться на южной стороне. В их движении появится корреляция.
Во-вторых, изменятся энергетические уровни, поскольку электроны отталкиваются друг от друга. Как велико будет это изменение? Мы можем сделать очень приближенный, но зато очень простой расчет. Предположим, что каждый из двух электронов находится на 1s-орбитали (средний радиус 0,39 Å) и что с обоюдного согласия они располагаются по разные стороны от ядра.
В таком случае энергия связи каждого электрона в атоме составляла бы 1254 ккал, как у единственного электрона в Не+. Каждый электрон находился бы на орбитали со средним радиусом 0,39 Å.
Слайд 6Тогда расстояние между ними вдвое превышало бы радиус орбитали (0,39 А). Энергия
Тогда расстояние между ними вдвое превышало бы радиус орбитали (0,39 А). Энергия

В действительности энергия отрыва электрона (потенциал ионизации) нейтрального атома гелия составляет не 1254 ккал (как это было бы в отсутствие межэлектронного отталкивания), а всего лишь 567 ккал. Как и предсказывал наш простенький расчет, энергии межэлектронного отталкивания весьма значительны — мы даже недооценили этот эффект на 40%.
На рис. 2.1 (ниже) приведена часть найденной экспериментально схемы энергетических уровней Не.
Слайд 8Рассмотрим 2s- и 2p-уровни. Эти ячейки расположены при значениях энергии, соответствующих таким
Рассмотрим 2s- и 2p-уровни. Эти ячейки расположены при значениях энергии, соответствующих таким

Внутренний 1s-электрон эффективно заслоняет (экранирует) половину заряда ядра.
Слайд 9Необходимо отметить и вторую особенность 2s- и 2p – орбиталей атома гелия.
Необходимо отметить и вторую особенность 2s- и 2p – орбиталей атома гелия.

Таким образом, 2s- и 2p-орбитали по-прежнему близки по энергиям, но равенство их энергий исчезает. Такое расщепление энергетических уровней с одинаковым главным квантовым числом в многоэлектронных атомах имеется всегда не только между s- и р- орбиталями, но и между р- и d-орбиталями. Это последнее расщепление имеет огромное значение, так как оно определяет последовательность элементов в периодической системе.
Слайд 10б) Атом лития
Возвращаясь к нашей простой модели с «выключенным» отталкиванием электронов, можно
б) Атом лития
Возвращаясь к нашей простой модели с «выключенным» отталкиванием электронов, можно

Этот вывод называется принципом Паули и представляет собой ключ к периодической системе. Мы сразу увидим его следствия, применив это правило к нейтральному атому лития.
Слайд 11Рис. 2.2. Схема энергетических уровней атомов водорода, гелия и лития. (Читателю следует
Рис. 2.2. Схема энергетических уровней атомов водорода, гелия и лития. (Читателю следует
Слайд 12Согласно принципу Паули, если два электрона уже заняли одну 1s-орбиталь, третий электрон
Согласно принципу Паули, если два электрона уже заняли одну 1s-орбиталь, третий электрон

Li (1s22s) → Li+ (1s2) + е– , Eион = 124 ккал. (2-1)
Но уже следующее по энергии состояние нейтрального атома лития (1s22р) обладает энергией ионизации всего 81 ккал/моль.
Li(1s22р) → Li+ (1s2) + е– , Eион = 81 ккал/моль. (2-2)
Слайд 13Так же как у атома гелия, 2s- и 2р-состояния не идентичны по
Так же как у атома гелия, 2s- и 2р-состояния не идентичны по

Было бы полезно исследовать, хотя бы приближенно, какой смысл имеют эти энергии ионизации. Предположим, что мы хотим построить одноэлектронный атом с энергией ионизации 2s-электрона, равной 124 ккал/моль. Из уравнения (1-11) можно узнать, какой заряд ядра Z* требуется для этого:
(2-3)
так что
Слайд 14Зная величину эффективного заряда ядра, с помощью уравнения (1-12) можно найти средний
Зная величину эффективного заряда ядра, с помощью уравнения (1-12) можно найти средний

Мы обнаруживаем здесь тот же эффект, с которым мы столкнулись в возбужденном состоянии атома гелия Не (1s2s). Внешний электрон ведет себя так, как будто заряд ядра намного меньше своей действительной величины.
В атоме лития 2s-электрон «ощущает» заряд ядра +3 через «экран», созданный двумя прочно связанными 1s-электронами. 2s-Электрон ведет себя так, как если бы заряд ядра составлял только 1,26.
Слайд 15Для лития в состоянии Li (1s22р) можно провести совершенно аналогичное рассуждение. 2p
Для лития в состоянии Li (1s22р) можно провести совершенно аналогичное рассуждение. 2p

Эффективный заряд ядра для 2р-электрона меньше, чем для 2s-электрона, хотя средние радиусы близки друг к другу. Причина такого отличия становится понятной, если взглянуть на рис. 1.13.
2s – Орбиталь «проникает» непосредственно к самому ядру, тогда как 2р – орбиталь имеет вблизи ядра узловую плоскость. Поэтому 2s-электрон может проникнуть сквозь созданный двумя 1s – электронами «экран» в атоме лития.
Слайд 16Ясно, что для 2р – электрона это гораздо сложнее. Вследствие узловых свойств
Ясно, что для 2р – электрона это гораздо сложнее. Вследствие узловых свойств

Эффект проникновения и объясняет расщепление между 2s- и 2p – уровнями, которое мы наблюдали на энергетических уровнях и гелия, и лития. Как уже было отмечено, этот эффект расщепления сохраняется и даже возрастает при переходе к боле высоким состояниям, таким, как 3s, 3p и 3d. Действительно, как будет видно в дальнейшем, именно комбинация принципа Паули (не больше двух электронов на одной орбитали) и расщепление орбиталей s, р и d позволяет понять закономерности периодической системы Менделеева.
Слайд 17в) Вперед к неону
Теперь, зная общие принципы, можно попытаться проследить за
в) Вперед к неону
Теперь, зная общие принципы, можно попытаться проследить за

Приведенных на рисунке орбиталей достаточно для размещения всех электронов, за исключением двух прочно связанных электронов на 1s-орбитали. Коль скоро нам известен принцип Паули, мы легко сможем понять и последовательность заполнения орбиталей вдоль периодов периодической системы. При переходе от лития к бериллию 2р-орбиталь нам не понадобится, так как второй электрон может поместиться на 2s-орбитали. Энергия ионизации у бериллия будет, конечно, выше, чем у лития, из-за большего заряда ядра бериллия.
Слайд 18Однако, когда мы переходим к бору, пятый электрон разместить ни на 1s-,
Однако, когда мы переходим к бору, пятый электрон разместить ни на 1s-,

Следующий элемент — углерод. Шесть электронов атома углерода размещаются следующим образом: два электрона занимают 1s-орбиталь, еще два — 2s-орбиталь, а оставшиеся два электрона располагаются на имеющихся трех 2р-орбиталях. Два из них могли бы занять 2рx – орбиталь, не вступая в противоречие с принципом Паули. Однако они оказались бы в одной и той же области пространства, сконцентрированной вдоль оси х, а это приводит к сильному меж электронному отталкиванию.
Слайд 19Положение становится более благоприятным, когда один электрон располагается на 2рx – орбитали,
Положение становится более благоприятным, когда один электрон располагается на 2рx – орбитали,

Аналогичные рассуждения справедливы и в случае азота. В соответствии с принципом Паули на 2р-орбиталях остаются три электрона, и, чтобы расстояние между ними было максимальным, эти три электрона занимают все три 2р-орбитали; по одному электрону на орбиталях 2рх , 2ру и 2рz. Энергия ионизации возрастает по сравнению с углеродом вследствие увеличения заряда ядра.
У кислорода, однако, последний электрон уже не может найти себе свободной 2р-орбитали. Ему приходится расположиться на 2р-орбитали, которая уже содержит один электрон. Межэлектронное отталкивание при этом, разумеется, резко возрастает и даже перекрывает эффект увеличения заряда ядра. Энергия отрыва электрона от кислорода меньше, чем у азота
Слайд 20Для рассмотрения фтора и неона не требуется вводить никаких, новых представлений. Их
Для рассмотрения фтора и неона не требуется вводить никаких, новых представлений. Их

На рис. 2.4 можно проследить за изменением энергий ионизации вдоль второго и третьего периодов периодической таблицы. При переходе от Н К Не энергия ионизации резко увеличивается, поскольку заряд ядра удваивается. Затем у лития она еще более резко уменьшается, так как принцип Паули вынуждает третий электрон перейти на орбиталь с более высокой энергией, 25-орбиталь. Далее, вдоль второго периода все семь электронов размещаются на 25- и 2р-орбиталях.
Здесь наблюдается общее повышение энергии ионизации, которое обусловлено увеличением заряда ядра; правда, имеются еще два небольших скачка, возникающих, во-первых, благодаря разности энергий 2s- и 2p – уровней и, во-вторых, в том случае, когда 2p-орбитали впервые заселяются двумя электронами, в результате усиления межэлектронного отталкивания.
Слайд 21Как показано на рис. 2.4, переход от неона к натрию сопровождается таким
Как показано на рис. 2.4, переход от неона к натрию сопровождается таким

Слайд 22Рис. 2.4. Изменение энергии ионизации в первом, втором и третьем периодах таблицы
Рис. 2.4. Изменение энергии ионизации в первом, втором и третьем периодах таблицы
Слайд 23 г) Эффективный заряд ядра во втором периоде
С помощью нашего одноэлектронного приближения*)
г) Эффективный заряд ядра во втором периоде
С помощью нашего одноэлектронного приближения*)
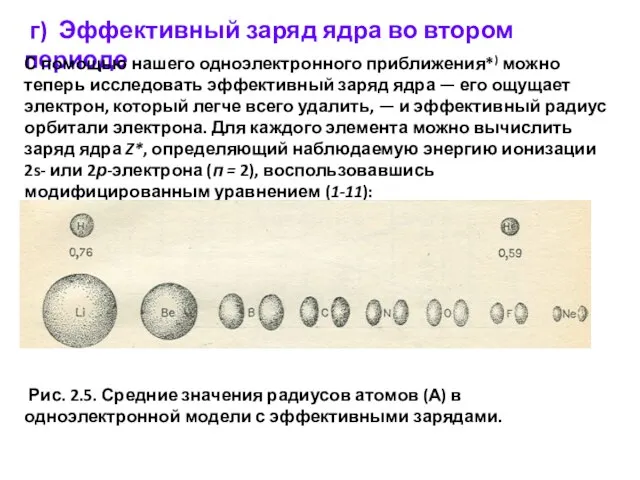
Рис. 2.5. Средние значения радиусов атомов (А) в одноэлектронной модели с эффективными зарядами.
Слайд 24(2 – 5)
Определив значение Z*, можно вычислить средний радиус одноэлектронных орбиталей с
(2 – 5)
Определив значение Z*, можно вычислить средний радиус одноэлектронных орбиталей с

(2 – 6)
Полученные таким путем результаты приведены в табл. 2.1. Как можно видеть, «чувствительность» самого слабосвязанного электрона к изменению заряда ядра возрастает вдоль периода периодической системы. Это возрастающее притяжение приводит к сжатию орбитали — средний радиус орбитали уменьшается (рис. 2.5). Значительную часть химических свойств можно объяснить двумя тенденциями, которые отражены в табл. 2.1 увеличением энергии ионизации и уменьшением размера орбиталей при переходе слева направо по периоду.
Слайд 25Таблица 2.1
Эффективный заряд ядра и радиус орбитали
в одноэлектронном приближении
Таблица 2.1
Эффективный заряд ядра и радиус орбитали
в одноэлектронном приближении
Слайд 26д) Спин электрона и принцип Паули
Тщательные измерения показывают, что электрон обладает не
д) Спин электрона и принцип Паули
Тщательные измерения показывают, что электрон обладает не

Слайд 27Как возникает магнитное поле электрона? В макромире магнитное поле возникает при движении
Как возникает магнитное поле электрона? В макромире магнитное поле возникает при движении

Такое объяснение в настоящее время общепринято. Эта простая .модель позволяет найти магнитное поле, обусловленное угловым моментом спина. Однако полученный результат оказывается вдвое больше экспериментально наблюдаемой величины. Для того чтобы понять это, вспомним, что при вращении электрона угловой момент определяется распределением массы, а магнитное поле — распределением заряда. Теперь мы сможем, хотя бы интуитивно, объяснить упомянутое выше расхождение. Если распределения массы и заряда не идентичны друг другу, классические вычисления дадут неверное соотношение между угловым моментом и магнитным полем, что и происходит в действительности.
Слайд 28Подробно рассматривать эту проблему нам не обязательно. Достаточно сказать, что спин электрона
Подробно рассматривать эту проблему нам не обязательно. Достаточно сказать, что спин электрона
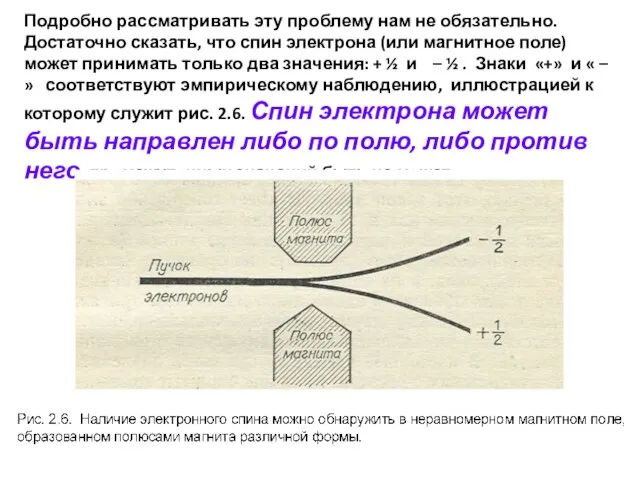
Слайд 29Величина ½ представляет собой коэффициент расхождения между экспериментом и простым расчетом для
Величина ½ представляет собой коэффициент расхождения между экспериментом и простым расчетом для

Исследования спектров атомов, помещенных в магнитное поле, показывают, что принцип Паули можно сформулировать более корректно: на одной орбитали могут одновременно находиться только два электрона, причем их спины должны быть противоположными.
При изображении орбитали в виде ячейки этому соответствует различный наклон черточки в кружке. Если на орбитали находится только один электрон —черточка проведена слева направо ,
Слайд 30то сюда же может прийти и второй — тогда мы проведем черточку
то сюда же может прийти и второй — тогда мы проведем черточку

К сожалению, этот закон природы имеет совершенно эмпирический характер, так же как и сам принцип Паули. Действительно, заселенности орбиталей и магнитные свойства атомов (и молекул) полностью подчиняются этому правилу: на орбитали находится не более двух электронов, и их спины противоположны.
По-видимому, это явление нельзя объяснить одним лишь магнитным притяжением, которое возникает между двумя антипараллельными магнитами, или соответственно отталкиванием, возникавшим при параллельной ориентации. В настоящее время это пытаются объяснить с помощью релятивистских эффектов, но такие сложные построения не дают решительно ничего нового для химии по сравнению с принципом Паули.
Слайд 312.2. ЭНЕРГИЯ ИОНИЗАЦИИ И ВАЛЕНТНЫЕ ЭЛЕКТРОНЫ
Существует явная зависимость между легкостью отрыва электрона
2.2. ЭНЕРГИЯ ИОНИЗАЦИИ И ВАЛЕНТНЫЕ ЭЛЕКТРОНЫ
Существует явная зависимость между легкостью отрыва электрона

а) Литий и бериллий
Легко понять, что удалить из атома второй электрон труднее, чём первый. Первый электрон отрывается от нейтрального атома, тогда как второй (и все последующие) необходимо оторвать от положительно заряженного иона. Однако даже с учетом этого имеются существенные отличия между разными атомами. Сравним, например, энергию ионизации (ккал/моль) газообразных атомов лития и бериллия.

 Презентация на тему Подгруппа кислорода
Презентация на тему Подгруппа кислорода  Сера - химический элемент и простое вещество
Сера - химический элемент и простое вещество Презентация на тему Сложные эфиры
Презентация на тему Сложные эфиры  Презентация на тему Общая характеристика подгруппы углерода
Презентация на тему Общая характеристика подгруппы углерода  Нефть - природный источник углеводородов
Нефть - природный источник углеводородов Белки́ (протеины, полипепти́ды)
Белки́ (протеины, полипепти́ды) Обращеннофазовая хроматография высокого разрешения RP HPLC
Обращеннофазовая хроматография высокого разрешения RP HPLC Алкины: получение и применение
Алкины: получение и применение Презентация на тему Экологические риски при добыче и переработке нефти
Презентация на тему Экологические риски при добыче и переработке нефти  Ковалентная химическая связь
Ковалентная химическая связь Основные понятия химической кинетики. Скорость химической реакции
Основные понятия химической кинетики. Скорость химической реакции Оксиды. Сложные вещества
Оксиды. Сложные вещества Презентация на тему Серная кислота, свойства серной кислоты
Презентация на тему Серная кислота, свойства серной кислоты  Презентация на тему Кристаллические решетки
Презентация на тему Кристаллические решетки  (Bu4N)2[Mo6I8(OOCCH3)6]. Синтез
(Bu4N)2[Mo6I8(OOCCH3)6]. Синтез Магний (Mg, Magnesium). Общая характеристика магния
Магний (Mg, Magnesium). Общая характеристика магния Аналитическая химия (ЛЕКЦИЯ 1)
Аналитическая химия (ЛЕКЦИЯ 1) Материаловедение и технология конструкционных материалов
Материаловедение и технология конструкционных материалов Получение антибиотиков
Получение антибиотиков Строение органических молекул. (Лекция 2)
Строение органических молекул. (Лекция 2) Порох. Сера, халькогены
Порох. Сера, халькогены Первые попытки классификации химических элементов
Первые попытки классификации химических элементов Структура електронної оболонки атома. Енергетичні рівні та підрівні
Структура електронної оболонки атома. Енергетичні рівні та підрівні Строение атома. История открытия
Строение атома. История открытия Закон эквивалентов
Закон эквивалентов Камень, скользящий на льду
Камень, скользящий на льду Спирты или алканолы
Спирты или алканолы Цинк (Zn). Свойства
Цинк (Zn). Свойства