Слайд 2Модель Андерсона – это модель, которая описывает микроскопический механизм возникновения локализованных магнитных

моментов на примесных атомах переходных металлов в немагнитной матрице. Для записи гамильтониана модели используется метод вторичного квантования
Слайд 3Вторичное квантование
Гамильтониан модели в представлении вторичного квантования выглядит следующим образом:

Слайд 4В итоге задача сводится к решению следующей системы:

Слайд 6
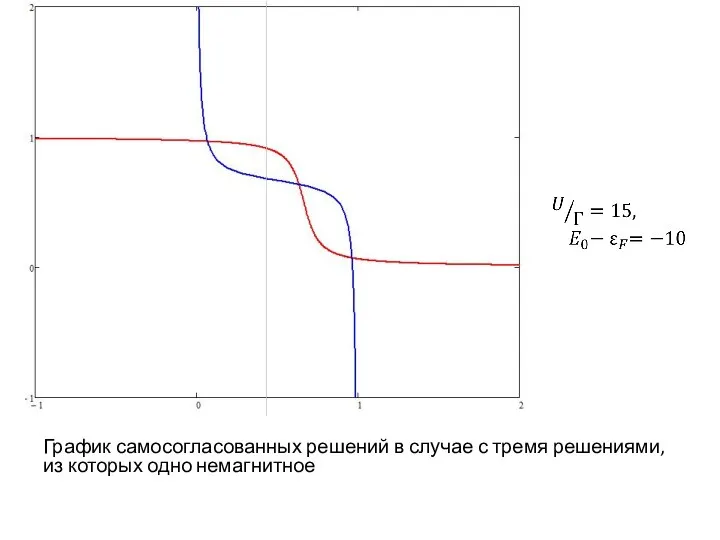
График самосогласованных решений в случае с тремя решениями, из которых одно немагнитное
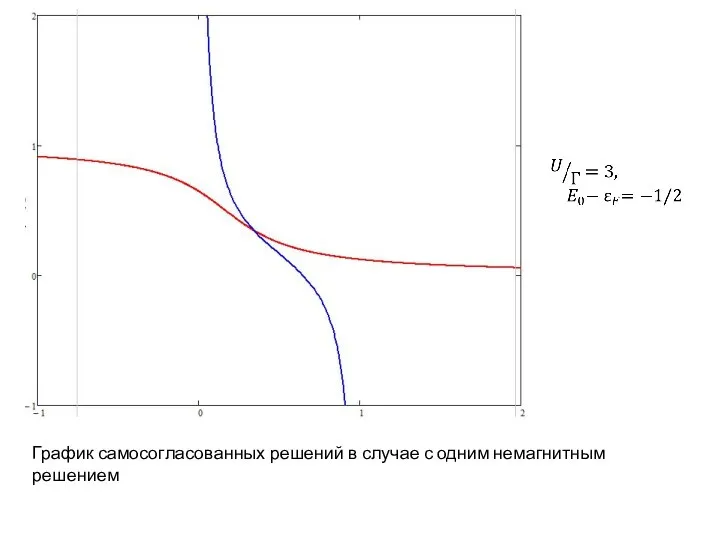
Слайд 7График самосогласованных решений в случае с одним немагнитным решением
Слайд 8В рассмотренной выше модели Андерсона уединенной примеси электроны были локализованы на узле.

Это значит, что параметр V, отвечающий за перескоки электронов с узла на узел, был равен нулю. В общем случае, когда в системе несколько атомов, расположенных недалеко друг от друга, это не так. Модель, учитывающая d-d-взаимодействия в периодической структуре носит название периодической модели Андерсона.
Слайд 9Число магнитных решений, при увеличении параметра U/Г меняется от одного до пяти.

При этом одно из решений, лежащее на оси симметрии, всегда является парамагнитным. Остальные решения являются симметричными относительно прямой и дают одинаковое по модулю значение магнитного момента.
Слайд 10
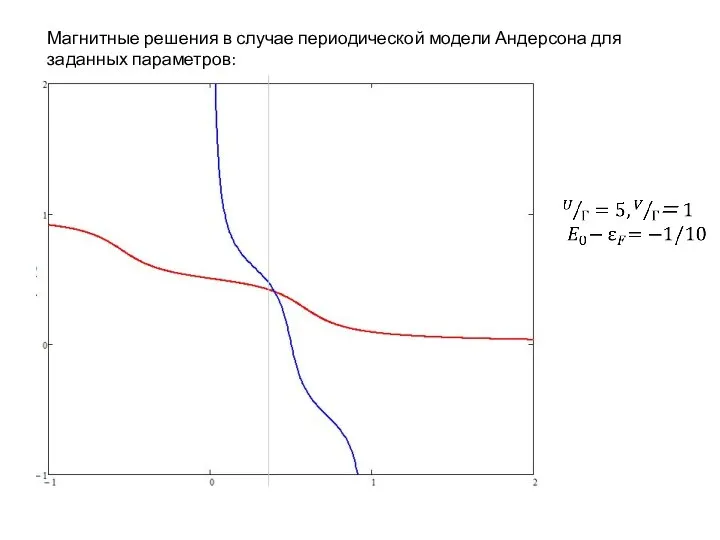
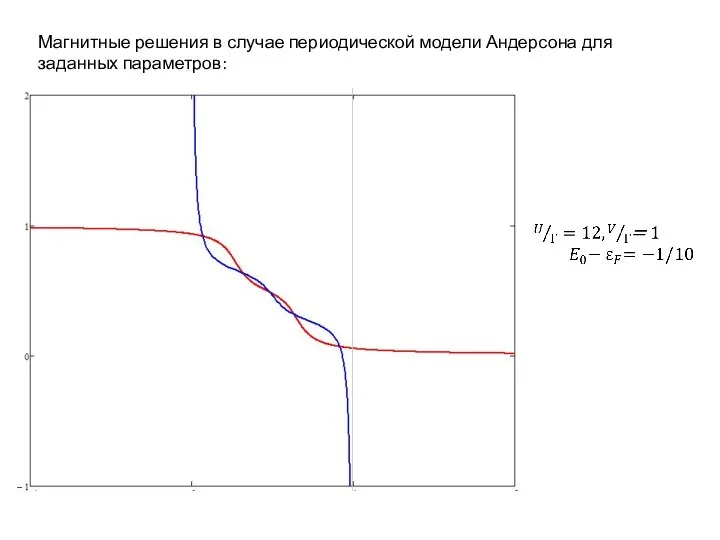
Магнитные решения в случае периодической модели Андерсона для заданных параметров:
Слайд 11
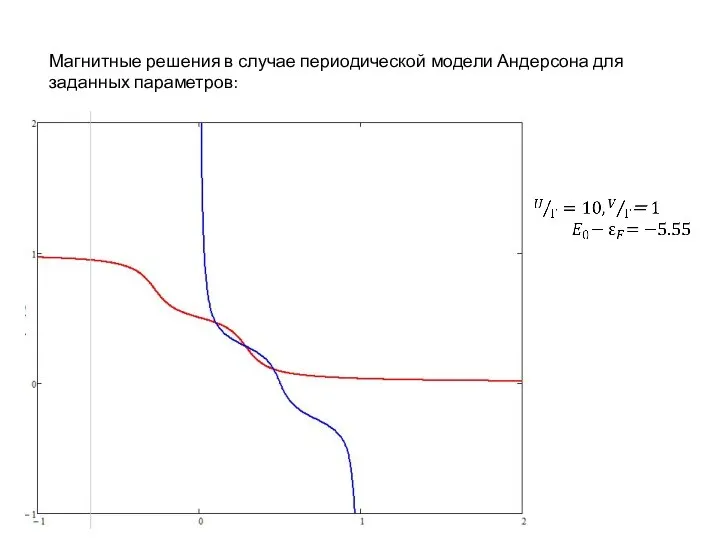
Магнитные решения в случае периодической модели Андерсона для заданных параметров:
Слайд 12
Магнитные решения в случае периодической модели Андерсона для заданных параметров:











 Исследовательский проект по химии на тему: Жесткость воды и способы ее устранения
Исследовательский проект по химии на тему: Жесткость воды и способы ее устранения Кислородсодержащие соединения азота. Оксиды азота
Кислородсодержащие соединения азота. Оксиды азота Биохимия. Основные классы соединений. Аминокислоты и Белки
Биохимия. Основные классы соединений. Аминокислоты и Белки Аймақтық мета морфизм тауж ыныстары
Аймақтық мета морфизм тауж ыныстары Степени окисления и формулы веществ
Степени окисления и формулы веществ Соли в свете теории электролитической диссоциации
Соли в свете теории электролитической диссоциации Силикатная промышленность
Силикатная промышленность Нанохімія та основи нанотехнологій
Нанохімія та основи нанотехнологій Презентация Повторение к СОЧ-10 кл (1)
Презентация Повторение к СОЧ-10 кл (1) Подгруппа углерода
Подгруппа углерода Неорганическая химия, часть 1
Неорганическая химия, часть 1 Анилин. Строение и свойства анилина
Анилин. Строение и свойства анилина Искусственные и синтетические полимеры
Искусственные и синтетические полимеры Признаки реакции
Признаки реакции ЛКМ на основе кремнийорганических соединений
ЛКМ на основе кремнийорганических соединений Химические методы количественного анализа веществ
Химические методы количественного анализа веществ Химический элемент Франций (Fr)
Химический элемент Франций (Fr) Органическая химия. Йенс Якоб Берцелиус (1779 - 1848)
Органическая химия. Йенс Якоб Берцелиус (1779 - 1848) Коррозия металлов
Коррозия металлов Приходченко ФЕР-2031
Приходченко ФЕР-2031 Кислород
Кислород Презентация на тему Великие химики
Презентация на тему Великие химики  Презентация на тему Подгруппа углерода и азота
Презентация на тему Подгруппа углерода и азота  Алюминий. Положение алюминия в периодической системе и строение его атома
Алюминий. Положение алюминия в периодической системе и строение его атома Арены. Бензол
Арены. Бензол Количество вещества. Молярная масса. Молярный объем
Количество вещества. Молярная масса. Молярный объем Химические средства защиты растений
Химические средства защиты растений Классификация неорганических веществ
Классификация неорганических веществ