Содержание
- 2. Индексы для плоскостей симметрии v – для плоскостей, расположенных вдоль единственной или главной оси симметрии, которые
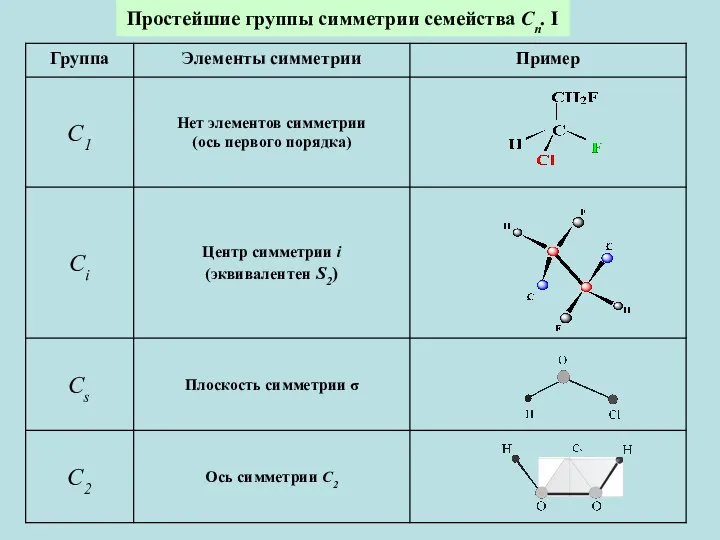
- 3. Простейшие группы симметрии семейства Сn. I
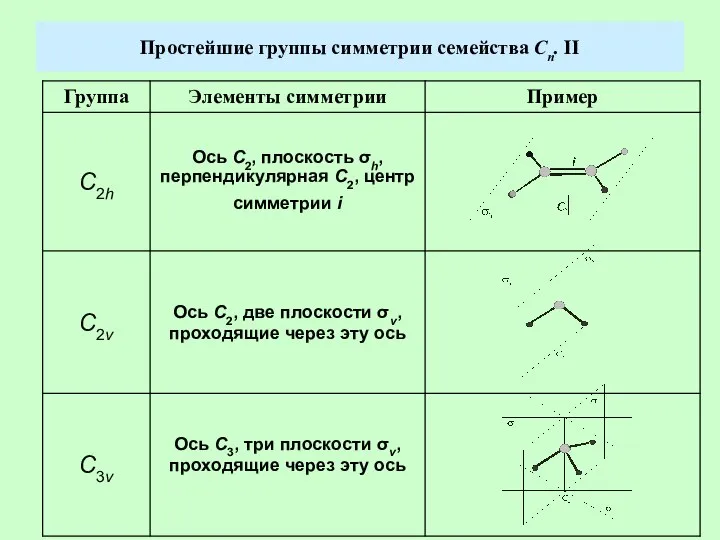
- 4. Простейшие группы симметрии семейства Сn. II
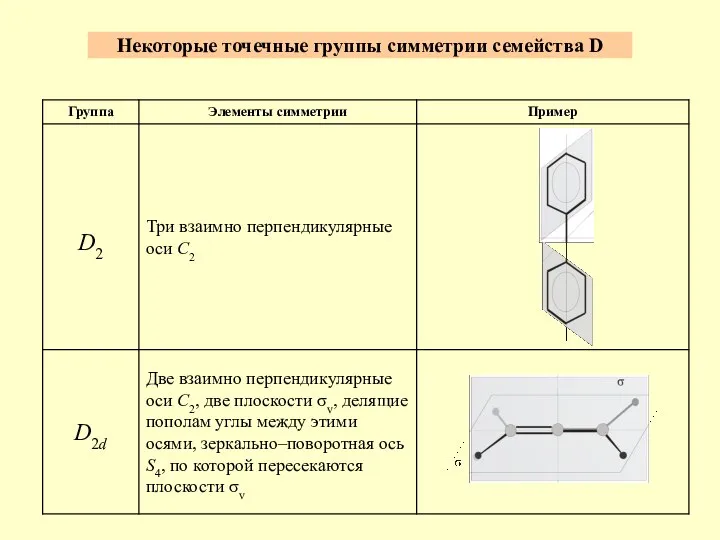
- 5. Некоторые точечные группы симметрии семейства D
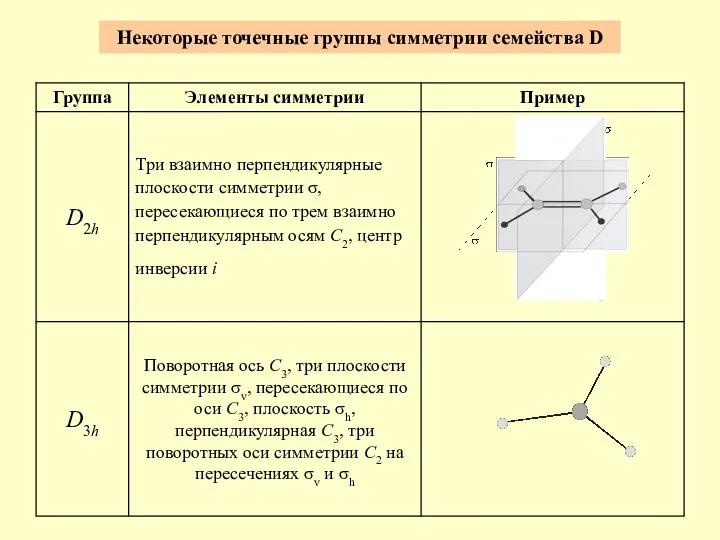
- 6. Некоторые точечные группы симметрии семейства D
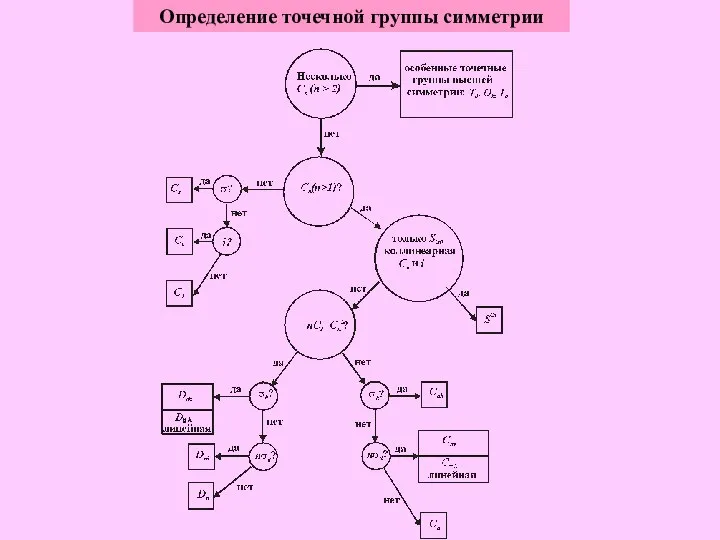
- 7. Определение точечной группы симметрии
- 8. Представления о симметрии нормальных колебаний Симметричное (A) по отношению к данной операции симметрии (s) – все
- 9. Дипольный момент Классическая теория 1. Дипольный момент есть вектор 2. Дипольный момент есть вектор причем Суммарный
- 10. Квантовая механика В состоянии, описываемом волновой функцией ψ дипольный момент определяется интегралом: Для молекулы, содержащей К
- 12. Скачать презентацию




 Химические свойства насыщенных альдегидов и кетонов (продолжение)
Химические свойства насыщенных альдегидов и кетонов (продолжение)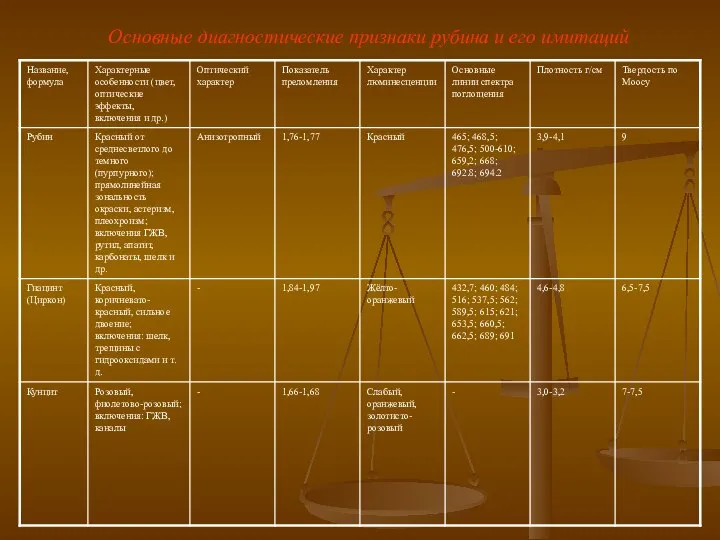 Основные диагностические признаки рубина и его имитаций
Основные диагностические признаки рубина и его имитаций Углерод
Углерод Химические реакции. Классификация
Химические реакции. Классификация Моющие и чистящие средства
Моющие и чистящие средства Влияние давления на скорость химических реакций с участием газов
Влияние давления на скорость химических реакций с участием газов Элемент астат
Элемент астат Презентация на тему Мусор
Презентация на тему Мусор  lektsia_7
lektsia_7 Текстуры руд
Текстуры руд Углеводы
Углеводы Углеводы, 2 часть. Лекция 15
Углеводы, 2 часть. Лекция 15 Презентация на тему Химический состав растений
Презентация на тему Химический состав растений  Амины. Аминокислоты
Амины. Аминокислоты Презентация на тему Галогены
Презентация на тему Галогены  Серная кислота
Серная кислота Хромофорная теория кислотно-основных индикаторов
Хромофорная теория кислотно-основных индикаторов Химические формулы. Относительная молекулярная масса. 8 класс
Химические формулы. Относительная молекулярная масса. 8 класс Явления
Явления Степень окисления. Электроотрицательность. Формулы бинарных соединений
Степень окисления. Электроотрицательность. Формулы бинарных соединений Основные свойства и опасности нефти. Безопасность для танкеров
Основные свойства и опасности нефти. Безопасность для танкеров Алюминий. Из истории открытия
Алюминий. Из истории открытия Технология производства органических лекарственных веществ. Препараты алифатического ряда: хлороформ, йодоформ, хлоральгидрат
Технология производства органических лекарственных веществ. Препараты алифатического ряда: хлороформ, йодоформ, хлоральгидрат Вещества в окружающей природе и в технике
Вещества в окружающей природе и в технике Амины. Аминокислоты
Амины. Аминокислоты Разработка методов синтеза гомогенных катализаторов оксосинтеза бутиловых спиртов
Разработка методов синтеза гомогенных катализаторов оксосинтеза бутиловых спиртов Свинец (plumbum)
Свинец (plumbum) Способы получения чистых веществ в лаборатории
Способы получения чистых веществ в лаборатории